Tight and taut immersions
The total absolute curvature $ \tau _ {a} ( f ) \leq \infty $
of an immersion of differentiability class $ C ^ {k} $,
$ k \geq 2 $,
$ f: M \rightarrow \mathbf R ^ {N} $,
of a closed connected $ n $-
manifold $ M $
in Euclidean $ N $-
space $ \mathbf R ^ {N} $(
cf. Immersion of a manifold) is expressed as an integral (a2) in terms of local invariants. It obeys
$$ \tag{a1 } \tau _ {a} ( f ) \geq \gamma \geq \beta = \sum \beta _ {i} . $$
Here $ \gamma $ is the infimum of $ \tau _ {a} ( f ) $ for all immersions of $ M $ into Euclidean space or for some special class of immersions, such as a component of the space of smooth imbeddings, and $ \beta _ {i} = \mathop{\rm rank} H _ {i} ( M ; \mathbf Z _ {2} ) $ is the $ i $- th Betti number for Čech homology with $ \mathbf Z _ {2} $ as coefficients (cf. Čech cohomology).
For a closed curve, $ \tau _ {a} ( f ) = \int | \rho d s | / \pi \geq \beta = 2 $, $ \rho $ is the curvature and $ s $ the arc length. For a $ C ^ {2} $surface $ M $ in $ \mathbf R ^ {3} $, $ \tau _ {a} ( f ) = \int | K d \sigma | / 2 \pi \geq \gamma = \beta = 4 - \chi $, $ K $ is the Gaussian curvature, $ d \sigma $ the area form, and $ \chi $ the Euler characteristic of $ M $. An immersion $ f $ is called tight if $ \gamma = \beta $ and if this $ f $ has minimal total absolute curvature $ \tau _ {a} ( f ) = \beta $, the lowest bound being attained. If, moreover, $ f( M) $ lies in the unit sphere $ S ^ {N- 1} = \{ {z \in \mathbf R ^ {N} } : {| z | = 1 } \} $, then the immersion $ f $ of $ M $ into $ S ^ {N- 1} $ is called taut. A taut immersion is always an imbedding.
The general definition of $ \tau _ {a} $ is as follows:
$$ \tag{a2 } \tau _ {a} ( f ) = { \frac{\int\limits _ { Q } | \nu ^ {*} ( \omega ) | }{ \mathop{\rm vol} ( S ^ {N- 1} ) } } = \int\limits _ { M } \tau _ {m} | d \sigma _ {m} | . $$
Here $ Q $ is the $ ( N- 1) $- manifold and bundle of unit normal vectors for $ m \in M $ at $ f( m) $, $ \nu $ is the natural projection by the Gauss mapping of $ Q $ into $ S ^ {N- 1} $, $ \omega $ is the volume element, an $ ( N- 1) $- form on $ S ^ {N- 1} $, $ \nu ^ {*} ( \omega ) $ the pull-back on $ Q $, and $ d \sigma _ {m} $ the volume element on $ M $ induced by the immersion into Euclidean space. The form $ \nu ^ {*} ( \omega ) $ is called the Lipschitz–Killing form. The well-defined density $ \tau _ {m} \geq 0 $ is the absolute Lipschitz–Killing density on $ M $. For surfaces (in $ \mathbf R ^ {3} $), $ \tau _ {m} = | K | / 2 \pi $. In general, $ \tau _ {a} ( f ) $ measures the area swept out by the normal vectors on the unit sphere of directions. Many homogeneous spaces, like $ \mathop{\rm SO} ( n) \subset \mathbf R ^ {n ^ {2} } $, all projective spaces and homogeneous Kähler manifolds, have tight (and even taut) imbeddings by their standard models in $ \mathbf R ^ {N} $ for some $ N $. (See below.)
The main problem is existence. One is interested also in the special properties of tight immersions for a given manifold $ M $.
Important is the following probabilistic definition:
$$ \tag{a3 } \tau ( f ) = {\mathsf E} _ {z} \mu _ {z} \leq \infty ,\ \ \mu _ {z} = \mu ( h _ {z} ) . $$
Here $ z \in S ^ {N- 1} $ is a unit vector, the gradient of the linear function $ z ^ {*} $ on $ \mathbf R ^ {N} $ with $ z ^ {*} ( z) = 1 $, $ h _ {z} = z ^ {*} \circ f $ is a height function on $ M $, $ \mu _ {z} $ is the number of non-degenerate critical points of $ h _ {z} $, and $ {\mathsf E} _ {z} $ the expectation (or mean) value for $ z \in S ^ {N- 1} $ with respect to the standard invariant measure on $ S ^ {N- 1} $.
For smooth immersions one has
$$ \tag{a4 } \tau = \tau _ {a} . $$
The property $ \tau ( f ) = \beta $, another definition of tight, permits the application of Morse theory. The inequality (a1) is, in particular, a consequence of the Morse inequality $ \mu _ {z} \geq \beta $, which holds for almost-all $ z \in S ^ {N- 1} $, as $ h _ {z} $ is non-degenerate for almost-all $ z $. It follows that an immersion is tight if every non-degenerate height function has $ \beta $ critical points. See Fig. cand Fig. d.

Figure: t092810c

Figure: t092810d
An imbedding of spaces $ A \subset B $ is called injective in $ \mathbf Z _ {2} $- homology if the induced homomorphism $ H _ {i} ( A, \mathbf Z _ {2} ) \rightarrow H _ {i} ( B, \mathbf Z _ {2} ) $ is injective for $ i \geq 0 $. Let $ H \subset \mathbf R ^ {N} $, with as boundary the hyperplane $ \partial H $, be a half-space of $ \mathbf R ^ {N} $. For example,
$$ H = H _ {z} ( t) = \{ {x \in \mathbf R ^ {N} } : {z ^ {*} ( x) \leq t } \} . $$
If $ f $ is a tight immersion and $ h _ {z} $ is a non-degenerate height function, then by Morse theory $ f ^ { - 1 } ( H _ {z} ( t)) \subset M $ is injective in $ \mathbf Z _ {2} $- homology. By continuity this injectivity then holds for every half-space $ H $. For smooth immersions of closed manifolds this half-space property is equivalent to tightness. However, this half-space definition can be applied in the larger context of continuous immersions or even mappings of manifolds and other compact topological spaces into $ \mathbf R ^ {N} $. An example is the tight "Swiss cheese" , an imbedded surface with boundary, see Fig. e. A tight mapping into $ \mathbf R $ is also called a perfect function.

Figure: t092810e

Figure: t092810f
For curves and closed surfaces, the half-space property reduces to $ f ^ { - 1 } ( H) $ being connected for every half-space $ H $. Equivalent is Banchoff's two-piece property, which says that every hyperplane $ \partial H $ in $ \mathbf R ^ {N} $ cuts $ M $ in at most two connected pieces. See the tight surfaces in Fig. c, Fig. d, and a non-tight curve in Fig. b.
The half-space definition places tightness in classical geometry and convexity theory. Thus it follows that tightness is a projective property (cf. Projective geometry), as it is clearly invariant under any projective transformation in $ \mathbf R ^ {N} $ that sends the convex hull $ {\mathcal H} ( f( M)) $ into $ \mathbf R ^ {N} $. Tautness as defined above is a conformal property (cf. Conformal geometry). It is invariant under any conformal (Möbius) transformation of $ S ^ {N-} 1 $ onto $ S ^ {N-} 1 $, which, in turn, is determined by a unique projective transformation in $ \mathbf R ^ {N} $ sending $ {\mathcal H} ( S ^ {N-} 1 ) $ onto $ {\mathcal H} ( S ^ {N-} 1 ) $.
In proofs an important role is played by Kuiper's fundamental theorem. For imbeddings it says: Top sets of tightly imbedded spaces are tight. A top set is the intersection with a supporting half-space or hyperplane in $ \mathbf R ^ {N} $.
Miscellaneous representative theorems, mainly mentioned for surfaces, are as follows.
Curves.
A tight closed curve in $ \mathbf R ^ {N} $ is plane and convex (W. Fenchel, 1929). The plane curve in Fig. a is not tight by every definition. A knotted curve in $ \mathbf R ^ {3} $ like the trefoil knot in Fig. b has $ \tau ( f ) > 2b( M) $. Equality with the infimum $ 2b( M) $ cannot be obtained (J. Milnor, 1950). Here $ b( M) $ is the bridge index of the knot $ M $. It is the smallest number of maxima a height function can have on a knot $ M $ admitting isotopy of the knot (cf. Knot theory). The trefoil knot in Fig. ahas $ b( M) = 2 $. On this knot every height function has at least two maxima but some height functions must have at least three by Milnor's bound above.
The first higher-dimensional theorem is due to S.S. Chern and J. Lashof (1957): A substantial (not in a hyper-plane) immersion of a closed $ n $- manifold $ f : M ^ {n} \rightarrow \mathbf R ^ {N} $, $ n \geq 1 $, of differentiability class $ C ^ \infty $ with $ \tau _ {a} ( f ) = 2 $, is a tight imbedding onto a convex hypersurface with $ N = n+ 1 $. The same conclusion is known for a continuous immersion with suitably defined $ \tau ( f ) = 2 $.
Surfaces.
If $ M $ is a non-orientable closed surface with Euler number $ \chi $, then no tight immersion into $ \mathbf R ^ {3} $ exists for $ \chi = 1 $ (projective plane) and $ \chi = 0 $ ( Klein bottle, cf. Klein surface), not even a continuous immersion. The case $ \chi = - 1 $( projective plane with one handle) was an open problem since 1960. F. Haab proved (in 1990) that this surface has in fact no tight smooth immersion in Euclidean space $ \mathbf R ^ {3} $. So, for every smooth immersion there exists a plane which cuts it in at least three pieces. All other surfaces have tight immersions into $ \mathbf R ^ {3} $. A tight torus $ ( \beta = 4) $ is depicted in Fig. c and a non-orientable tight surface with $\chi = - 2 $, $ \beta = 6 $ in Fig. d. The following theorems show that higher codimension and analyticity drastically restrict the possibility and nature of tight immersions. Also, differentiability is restrictive in comparison with continuous or piecewise-linear immersions.
A smooth tight substantial closed surface in $ \mathbf R ^ {N} $, for $ N \geq 5 $, is necessarily an (algebraic) Veronese surface (topologically a real projective plane, cf. also Veronese mapping) in $ \mathbf R ^ {5} $, unique up to projective transformations in $ \mathbf R ^ {5} $( N.H. Kuiper, 1960).
T. Banchoff (1965) suggested, however, and W. Kühnel (1980, see [a3]) proved, that except for the Klein bottle, a tight substantial polyhedral surface in $ \mathbf R ^ {N} $ exists exactly for $ N + 1 \leq ( 7 + \sqrt {49 - 24 \chi } ) /2 $. This number is Heawood's chromatic number, known from the map-colour theorem. The same upper bound seems to hold for continuous tight immersions.
In this context there is another remarkable theorem. A substantial tight continuous immersion of the real projective plane into $ \mathbf R ^ {N} $, $ N \geq 5 $, is necessarily an imbedding into $ \mathbf R ^ {5} $ onto either the algebraic Veronese surface or onto Banchoff's six-vertex polyhedral surface [a11]. Every smooth immersion of a surface with $ \chi = 2 $ or $ \chi < - 9 $ into $ \mathbf R ^ {3} $ is regularly isotopic to a tight immersion (U. Pinkall, [a15]). For the other surfaces the results are not yet complete. Every orientable surface with $ \chi \leq 0 $ has a smooth substantial tight imbedding in $ \mathbf R ^ {4} $, but it
be analytic except for the torus (G. Thorbergsson, [a19]). Every smooth imbedded knotted orientable surface in $ \mathbf R ^ {3} $ has total absolute curvature $ \geq \beta + 4 = 8 - \chi = 6 + 2g $, and equality cannot be attained if genus $ g = 1 $ or $ 2 $. For genus $ g \geq 3 $, however, Kuiper and W.F. Meeks [a10] proved that there do exist "isotopy-tight" knotted surfaces with $ \tau ( f ) = \beta + 4 $. An example of a knotted surface of genus $ 3 $, $ \tau ( f ) = 12 $ is depicted in Fig. e. It is obtained from two linked tight tori by two connecting handles of non-positive Gaussian curvature $ K $. For this surface every non-degenerate height function has $ 12 $ critical points.
Smooth immersions of surfaces in $ \mathbf R ^ {3} $ form a subclass of the smooth stable mappings $ f: M \rightarrow \mathbf R ^ {3} $. In that class every surface has a tight stable mapping into $ \mathbf R ^ {3} $, hence with total absolute curvature equal to
$$ \tau ( f ) = \beta = 4 - \chi ( M) = \ \int\limits { \frac{| K d \sigma | }{2 \pi } } . $$
Tight analytic surfaces in $ \mathbf R ^ {3} $ are isometrically rigid in the class of analytic surfaces (A.D. Aleksandrov, 1938; see [a3], p. 81, and Rigidity). Hardly anything more is known about $ C ^ {2} $- rigidity of non-convex smooth closed surfaces in $ \mathbf R ^ {3} $. However, by Kuiper's theorem (1955), no smooth closed surface in $ \mathbf R ^ {3} $ is $ C ^ {1} $- isometrically rigid. A surprising tight four-dimensional manifold in $ \mathbf R ^ {8} $ is Kühnel's topological imbedding of the complex projective plane $ M ^ {4} = P ( \mathbf C , 2) $ into the $ 4 $- skeleton of a simplex in $ \mathbf R ^ {8} $[a9]. The image is a triangulation of $ M $ with $ 9 $ vertices.
Taut imbeddings deserve a separate discussion. Let $ M $ be a compact connected space. The given extrinsic definition of tautness for $ M \subset S ^ {n} \subset \mathbf R ^ {n+} 1 $ in the $ n $- sphere $ S ^ {n} $, namely by the property that $ M $ is tight in $ \mathbf R ^ {n+} 1 $, evidently determines (with the half-space definition of tight) the following intrinsic definition. The subspace $ M \subset S ^ {n} $ is taut in $ S ^ {n} $ if the inclusion $ B _ {S} \cap M \subset M $ is injective in $ \mathbf Z _ {2} $- homology for every (round) ball $ B _ {S} $ in $ S ^ {n} $. By stereographic projection from a point $ z \in S ^ {n} \setminus M $ into a Euclidean $ n $- space $ \mathbf R ^ {n} $ orthogonal to the vector $ z $, one obtains the following definition of tautness in $ \mathbf R ^ {n} $. A compact subspace $ M \subset \mathbf R ^ {n} $ is taut if and only if $ M $ contains no open set of $ \mathbf R ^ {n} $, and the imbedding $ B \cap M \subset M $ is injective in $ \mathbf Z _ {2} $- homology, with $ B $ a round ball or the complement of a round ball in $ \mathbf R ^ {n} $. Then taut implies tight. A taut subspace of the plane is either a circle or a round disc, from which an everywhere-dense union of disjoint open round discs is deleted (a "limit Swiss cheese" ). Banchoff's plane Swiss cheese in Fig. e is tight but not taut, although every circle does cut it in at most two pieces, but one piece could be not injective in homology. While excluding exotic examples by an ANR-assumption, it is conjectured that every compact taut absolute neighbourhood retract in $ \mathbf R ^ {n} $( cf. also Absolute retract for normal spaces; Retract of a topological space) is a smooth manifold. This is known for $ n = 3 $. See [a8].
The customary definitions of a smooth taut manifold $ M $ in $ \mathbf R ^ {N} $ are as follows: a) every non-degenerate distance function $ h _ {x} $ has $ \beta ( M) $ critical points; and b) every round ball in $ \mathbf R ^ {N} $ meets $ M $ in a subset that is $ \mathbf Z _ {2} $- homology injective in $ M $. These definitions make sense and are also used for proper submanifolds of $ \mathbf R ^ {N} $ that are not necessarily compact (see [a3]). But in that case tight is not defined and so tightness is not a consequence.
For a smooth proper submanifold $ M $ in $ \mathbf R ^ {N} $, the customary requirement of tautness is a very strong condition. The only taut closed surfaces in $ \mathbf R ^ {N} $ are, up to a Möbius transformation, the following: homogeneous spaces, the round $ S ^ {2} $, the standard torus $ S _ {a} ^ {1} \times S _ {b} ^ {1} \subset \mathbf R ^ {2} \times \mathbf R ^ {2} = \mathbf R ^ {4} $( $ a $ and $ b $ are radii), and the standard Veronese surface (projective plane) in $ S ^ {4} \subset \mathbf R ^ {5} $. Each of these models is a homogeneous space by motions of $ \mathbf R ^ {n} $. Taut tori in $ \mathbf R ^ {3} $ are Dupin cyclides (cf. Dupin cyclide). The diffeomorphism classes of all taut $ 3 $- manifolds in Euclidean spaces were found in [a17].
T. Ozawa [a14] proved that every connected set of critical points of a distance function $ h _ {x} $ or $ h _ {z} $ on a closed taut manifold $ M $ is itself a taut submanifold. The manifold $ M $ then contains many low-dimensional taut submanifolds, like circles, and tends to be special for this reason. Tautness plays an important role in differential geometry, in the study of the following kinds of spaces.
1) Orbits of isotropy representations of symmetric spaces, also called $ R $- spaces (Kobayashi–Takeuchi), are taut submanifolds. They are, of course, homogeneous spaces and their cohomology was computed using (degenerate) tight height functions in a classic paper of R. Bott and H. Samelson [a1].
2) Closed isoparametric submanifolds. A compact submanifold $ M ^ {n} \subset \mathbf R ^ {N} $ is called isoparametric if it has a flat normal bundle and the principal curvatures in the direction of any parallel normal vector field are constant. Then $ M ^ {n} $ lies in a sphere $ S ^ {N-} 1 $, but need not be homogeneous for codimension $ N - n = 2 $, [a5]. If $ M $ is irreducible with codimension $ N - n \geq 3 $, then $ M $ is an $ R $- space, [a20]. Isoparametric submanifolds are taut. They form a generalization of $ R $- spaces and their cohomology can likewise be calculated from their associated marked Dynkin diagrams ([a6]). The concepts of taut imbedding and isoparametric submanifold generalize to the Hilbert space setting [a16]. Examples are the infinite-dimensional flag manifolds. Finally, a remarkable result due to H.-F. Münzer [a12] is that for an isoparametric hypersurface $ M ^ {n} $ in a sphere $ S ^ {n+} 1 $, the number of distinct principal curvatures must be $ 1 $, $ 2 $, $ 3 $, $ 4 $, or $ 6 $.
3) A submanifold $ M $ in $ \mathbf R ^ {N} $ is called totally focal if every distance function $ h _ {x} $( $ x \in \mathbf R ^ {N} $) either has on $ M $ all critical points non-degenerate or all critical points degenerate. In combined efforts over several years of T.E. Cecil and P.J. Ryan, S. Carter and A. West [a4], the latter finally obtained the result that closed totally focal manifolds are the same as closed isoparametric submanifolds.
Note that any Möbius transform, or stereographic projection, or tubular $ \epsilon $- neighbourhood boundary of a taut submanifold, like those mentioned above, is taut. Tautness is also invariant under the group of Lie sphere transformations, which contains the Möbius group as a subgroup [a2]. The product of two taut imbeddings is taut, and cylinders and surfaces of revolution built from taut imbeddings are taut (see [a3] and [a15]). All closed taut submanifolds that are now known (1990) have been obtained by these and some other new constructions (see [a18] and [a13]). Perhaps these exhaust all possibilities. For a wealth of other results and generalizations see the references.
References
| [a1] | R. Bott, H. Samelson, "Applications of the theory of Morse to symmetric spaces" Amer. J. Math. , 80 (1958) pp. 964–1029 MR0105694 Zbl 0101.39702 |
| [a2] | T.E. Cecil, S.S. Chern, "Tautness and Lie sphere geometry" Math. Ann. , 278 (1987) pp. 381–399 MR0909233 Zbl 0635.53029 |
| [a3] | T.E. Cecil, P.J. Ryan, "Tight and taut immersions of manifolds" , Pitman (1985) MR0781126 Zbl 0596.53002 |
| [a4] | S. Carter, A. West, "Isoparametric and totally focal submanifolds" Proc. London Math. Soc. , 60 (1990) pp. 609–624 MR1044313 Zbl 0663.53045 |
| [a5] | D. Ferus, H. Karcher, H.F. Münzer, "Clifford Algebren und neue isoparametrische Hyperflächen" Math. Z. , 177 (1981) pp. 479–502 MR624227 |
| [a6] | W.Y. Hsiang, R.S. Palais, C.L. Terng, "The topology of isoparametric submanifolds" J. Diff. Geom. , 27 (1988) pp. 423–460 MR0940113 Zbl 0618.57018 |
| [a7] | N.H. Kuiper, "Tight embeddings and maps" W.Y. Hsiang (ed.) et al. (ed.) , The Chern Symposium (1979) , Springer (1980) pp. 97–145 MR0609559 Zbl 0461.53033 |
| [a8] | N.H. Kuiper, "Taut sets in three-space are very special" Topology , 23 (1984) pp. 323–336 MR0770568 Zbl 0578.53044 |
| [a9] | W. Kühnel, T. Banchoff, "The 9-vertex complex projective plane" The Math. Intelligencer , 5 : 3 (1983) pp. 11–22 MR0737686 Zbl 0534.51009 |
| [a10] | N.H. Kuiper, W.F., III Meeks, "Total curvature for knotted surfaces" Invent. Math. , 77 (1984) pp. 25–69 MR0751130 Zbl 0553.53034 |
| [a11] | N.H. Kuiper, W.F. Pohl, "Tight topological embedding of the real projective plane in 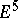 " Invent. Math. , 42 (1977) pp. 177–199 MR0494122 " Invent. Math. , 42 (1977) pp. 177–199 MR0494122 |
| [a12] | H.-F. Münzner, "Isoparametrische Hyperflächen in Sphären II" Math. Ann. , 256 (1981) pp. 215–232 MR0620709 Zbl 0438.53050 |
| [a13] | R. Miyaoka, T. Ozawa, "Construction of taut embeddings and the Cecil–Ryan conjecture" , Proc. 1988 Symp. Differential geometry , Acad. Press (1990) |
| [a14] | T. Ozawa, "On critical sets of distance functions to a taut submanifold" Math. Ann. , 276 (1986) pp. 91–96 MR0863709 |
| [a15] | U. Pinkall, "Tight surfaces and regular homotopy" Topology , 25 (1986) pp. 475–481 MR0862434 Zbl 0605.53027 |
| [a16] | R.S. Palais, C.L. Terng, "Critical point theory and submanifold geometry" , Lect. notes in math. , 1353 , Springer (1988) MR0972503 Zbl 0658.49001 |
| [a17] | U. Pinkall, G. Thorbergsson, "Taut 3-manifolds" Topology , 28 (1989) pp. 389–402 MR1030983 Zbl 0686.53050 |
| [a18] | U. Pinkall, G. Thorbergsson, "Deformations of Dupin hypersurfaces" Proc. Amer. Math. Soc. , 107 (1989) pp. 1037–1043 MR0975655 Zbl 0682.53061 |
| [a19] | G. Thorbergsson, "Tight analytic surfaces" Topology (Forthcoming) MR1113686 Zbl 0727.57031 |
| [a20] | G. Thorbergsson, "Isoparametric foliations and their buildings" Ann. of Math. , 31 (1991) pp. 429–446 MR1097244 Zbl 0727.57028 |
Tight and taut immersions. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tight_and_taut_immersions&oldid=53922

