Differential geometry

of curves and surfaces

A branch of geometry dealing with geometrical forms, mainly with curves and surfaces, by methods of mathematical analysis. In differential geometry the properties of curves and surfaces are usually studied on a small scale, i.e. the study concerns properties of sufficiently small pieces of them. Properties of families of curves and surfaces are also studied (see, for example, Congruence; Web).

Differential geometry arose and developed in close connection with mathematical analysis, the latter having grown, to a considerable extent, out of problems in geometry. Many geometrical concepts were defined prior to their analogues in analysis. For instance, the concept of a tangent is older than that of a derivative, and the concepts of area and volume are older than that of the integral.

Differential geometry first appeared in the 18th century and is linked with the names of L. Euler and G. Monge. The first synoptic treatise on the theory of surfaces was written by Monge (Une application d'analyse à la géométrie, 1795). In 1827 a study under the (English) title A general study on curved surfaces was published by C.F. Gauss; this study laid the foundations of the theory of surfaces in its modern form. From that time onwards differential geometry ceased to be a mere application of analysis, and has become an independent branch of mathematics.

The discovery of non-Euclidean geometry by N.I. Lobachevskii in 1826 played a major role in the development of geometry as a whole, including differential geometry. Lobachevskii rejected in fact the a priori concept of space, which was predominating in mathematics and in philosophy. He found that spaces different from Euclidean spaces exist. This idea of Lobachevskii was reflected in numerous mathematical studies. Thus, in 1854 B. Riemann published his course Über die Hypothesen, welche der Geometrie zuGrunde liegen and thus laid the foundations of Riemannian geometry, the application of which to higher-dimensional manifolds is related to the geometry of $ n $- dimensional space similarly as the relation between the interior geometry of a surface and Euclidean geometry on a plane.

The group-theoretic view exposed by F. Klein in 1872 in his Erlangen program — viz. that geometry is the study of invariants under groups of transformations — was developed by E. Cartan in relation to differential geometry. Cartan established the theory of spaces with projective connections and affine connections (cf. Affine connection; Projective connection).

In Russia a school of differential geometry was established by F. Minding and K.M. Peterson. Their studies largely concern the problems of isometric deformation (cf. Deformation, isometric) of surfaces, i.e. such continuous deformations of surfaces during which the interior geometry remains invariant. These studies were continued by many Russian and Soviet geometers.

The theory of curves.

The major subject of the theory of curves are the so-called differentiable curves. These are curves which can locally be specified by equations of the type

$$ \tag{1 } x = x ( t) ,\ y = y ( t) ,\ z = z ( t) , $$

where $ x ( t) , y( t) , z( t) $ are sufficiently regular functions of a parameter $ t $. The degree of differentiability of the curve is given by the degree of differentiability of $ x ( t) , y ( t) $ and $ z ( t) $. For one and the same curve there are uncountably many ways of parametric description of the type (1). Of these, the so-called natural parametrization, in which the length of an arc of the curve, counted from some given point, serves as the parameter, is especially important. A point on a curve is said to be regular if, by a suitable choice of a Cartesian coordinate system $ x , y , z $, the curve can be defined, in a neighbourhood of that point, by equations of the form

$$ y = y ( x) ,\ z = z ( x) , $$

where $ y ( x) $ and $ z ( x) $ are differentiable functions. Otherwise it is called singular (cf. Singular point). In differential geometry the study of a curve mainly concerns a neighbourhood of a regular point. For a point on a curve defined by the general equation (1) to be regular, it is necessary and sufficient that the inequality

$$ {x } ^ \prime 2 + {y } ^ \prime 2 + {z } ^ \prime 2 \neq 0 $$

holds at this point.

A number of fundamental concepts in the theory of curves is based on the concept of contact of sets, which may be explained as follows. Let $ M $ and $ m $ be two sets with a common point $ 0 $. One says that the sets $ M $ and $ m $ have a contact of order $ \alpha \geq 1 $ at $ 0 $ if

$$ \frac{\delta ( X) }{| X 0 | ^ \alpha } \rightarrow 0 $$

as $ X \rightarrow 0 $, where $ \delta ( X) $ is the distance of a point $ X $ of the set $ M $ from $ m $. If $ M $ is a curve while $ m $ is a straight line passing through a point $ 0 $ of the curve, then if $ \alpha \geq 1 $, the contact condition defines $ m $ to be the tangent to the curve at $ 0 $( Fig. a).

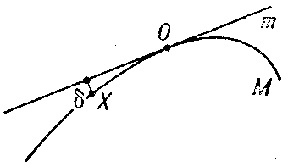
Figure: d032170a

A smooth (differentiable) curve has a definite tangent at each of its points. The direction of the tangent at a point $ t _ {0} $ of a curve specified by (1) coincides with the direction of the vector $ [ x ^ \prime ( t _ {0} ) , y ^ \prime ( t _ {0} ) , z ^ \prime ( t _ {0} ) ] $. In differential geometry the equations of the tangent are derived for the various ways in which the curve is analytically specified. In particular, if the curve is defined by equations (1), the equations of the tangent at the point corresponding to the value $ t _ {0} $ of the parameter are

$$ ( X , Y , Z ) = \ ( x _ {0} + u x _ {0} ^ \prime ,\ y _ {0} + u y _ {0} ^ \prime ,\ z _ {0} + u z _ {0} ^ \prime ) ,\ \ u \in \mathbf R , $$

where the subscript "0" indicates the values of the functions $ x , y $ and $ z $ and their derivatives at the point $ t _ {0} $. If $ m $ is a plane passing through a point $ 0 $ of the curve $ M $, the contact condition for $ \alpha \geq 2 $ defines the osculating plane to the curve (Fig. b).

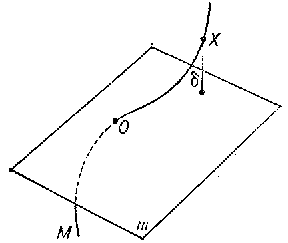
Figure: d032170b

A twice differentiable curve has an osculating plane at each of its points. It is either unique or else any plane passing through the tangent to the curve is osculating.

When moving along a curve, the tangent to the curve undergoes a rotation. The velocity of this rotation, as the motion along the curve takes place at velocity one, is called the curvature of the curve. If the curve has been parametrized as in (1), its curvature is given by the formula

$$ k _ {1} = \frac{| \mathbf r ^ \prime ( t) \times \mathbf r ^ {\prime\prime} ( t) | }{| \mathbf r ^ \prime ( t) | ^ {3 / 2 } } , $$

where $ \mathbf r ( t) $ is the vector function with coordinates $ x ( t) , y ( t) , z ( t) $. Straight lines, and only straight lines, have a curvature which is everywhere equal to zero. A twice differentiable curve has a unique osculating plane at all points at which the curvature is non-zero. As one moves along the curve in a neighbourhood of such a point, the osculating plane rotates, and the tangent to the curve is the instantaneous axis of this rotation. The velocity of rotation of the osculating plane, for a uniform motion along the curve at velocity one, is called the torsion of the curve. The sign of the torsion depends on the direction of the rotation. A thrice differentiable curve has a definite torsion at each of its points where the curvature is non-zero. If the curve has been parametrized as in (1), its torsion is given by the formula

$$ k _ {2} = \frac{( \mathbf r ^ \prime , \mathbf r ^ {\prime\prime} , \mathbf r ^ {\prime\prime\prime} ) }{| \mathbf r ^ \prime \times \mathbf r ^ {\prime\prime} | ^ {2} } . $$

The torsion of a planar curve is zero at all points. Conversely, a curve with torsion identically equal to zero is planar.

A straight line perpendicular to the tangent and passing through the point of contact is known as a normal to the curve. The normal lying in the osculating plane is called the principal normal, while the normal which is perpendicular to the osculating plane is known as the binormal. The figure constructed out of the tangent, the principal normal and the binormal, and also given by the three planes containing pairwise these straight lines, is called the Frénet frame (natural frame; also called Frénet trihedron and natural trihedron). If the edges of this frame at the given point are considered as the axes of a Cartesian coordinate system, then the equation of the curve in a natural parametrization in a neighbourhood of this point will have the form

$$ x = s + \dots ,\ y = \frac{k _ {1} }{2} s ^ {2} + \dots ,\ \ z = - \frac{k _ {1} k _ {2} }{6} s ^ {3} + \dots , $$

where $ k _ {1} $ and $ k _ {2} $ are the curvature and the torsion of the curve at this point. Fig. c represents the projections of the curve on the faces of the natural frame near a point with a non-zero curvature and a non-zero torsion.

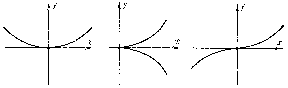
Figure: d032170c

The unit vectors $ \pmb\tau , \pmb\nu , \pmb\beta $ of the tangent, of the principal normal and of the binormal to a curve vary during a motion along the curve. A suitable choice of directions of these vectors, in accordance with the definitions of the curvature and the torsion, yields the formulas

$$ \tag{2 } \pmb\tau ^ \prime = k _ {1} \pmb\nu ,\ \pmb\beta ^ \prime = k _ {2} \pmb\nu ,\ \pmb\nu ^ \prime = - k _ {1} \pmb\tau - k _ {2} \pmb\beta , $$

where the prime indicates differentiation with respect to the arc of the curve. The formulas (2) are known as the Frénet formulas. A curve with non-zero curvature is defined, up to its location in space, by specifying its curvature and its torsion as functions of the arc length $ s $ of the curve. This is why the system of equations

$$ k _ {1} = k _ {1} ( s) ,\ k _ {2} = k _ {2} ( s) $$

is also known as the system of natural equations of the curve (cf. Natural equation).

Planar curves, i.e. curves lying in a plane, are an important class of curves. In the case of planar curves it is possible to distinguish between the directions of rotation of the tangent moving along the curve, so that the curvature can be given a sign depending on the direction of this rotation. The curvature of a planar curve defined by the equations $ x = x ( t) , y = y ( t) $ is given by the formula

$$ k = \pm \frac{y ^ {\prime\prime} x ^ \prime - x ^ {\prime\prime} y ^ \prime }{( {x } ^ \prime 2 + {y } ^ \prime 2 ) ^ {3 / 2 } } . $$

The plus or minus sign is chosen in accordance with a convention, but must be the same all along the curve. The important concept of the osculating circle is introduced for planar curves. This is a circle with a contact of order $ \alpha \geq 2 $ with the curve (Fig. d).

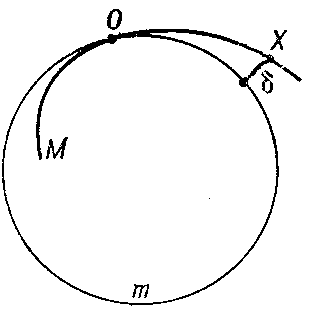
Figure: d032170d

Figure: d032170e

It exists at each point of a twice differentiable curve with a non-zero curvature. The centre of the osculating circle is known as the centre of curvature, while its radius is known as the radius of curvature. The radius of curvature is the quantity inverse to the curvature. The locus of the centres of curvatures of a curve is known as the evolute. The curve which orthogonally intersects the tangents to the curve is called the evolvent (cf. Evolvent of a plane curve) (Fig. e). The evolute of the evolvent of a curve is the curve itself.

A curve $ \gamma $ is called the envelope of a family of curves $ \gamma _ \alpha $, depending on a parameter $ \alpha $, if at each of its points it is tangent to at least one curve of the family, and if each of its segments is tangent to an infinite set of these curves.

The theory of surfaces and its generalizations.

The theory of surfaces usually deals with differentiable surfaces. These are surfaces which can be locally defined by equations of the type

$$ \tag{3 } x = x ( u , v ) ,\ y = y ( u , v ) ,\ \ z = z ( u , v ) , $$

where $ x ( u , v ) , y ( u , v ) , z ( u , v ) $ are differentiable functions of the parameters $ u $ and $ v $. The degree of differentiability of the surface is given by the corresponding degree of differentiability of these functions. A surface has uncountably many ways in which it can be defined by parametric equations such as (3). A point of a surface is said to be regular (ordinary) if, in a neighbourhood of it, a suitable choice of the coordinates $ x , y , z $ enables one to give the surface in the form

$$ \tag{4 } z = z ( x , y ) , $$

where $ z ( x , y ) $ is a smooth function; otherwise, the point of the surface is said to be singular. In differential geometry the study of the surface is mainly conducted in a neighbourhood of the regular (ordinary) points. For a point $ ( u _ {0} , v _ {0} ) $ of a surface given by the equations (3) to be regular, it is necessary and sufficient that the rank of the matrix

$$ \left ( \begin{array}{lcr} x _ {u} &y _ {u} &z _ {u} \\ x _ {v} &y _ {v} &z _ {v} \\ \end{array} \right ) $$

at this point be equal to two. If a surface is given by equations of the type (3), it is usually assumed, without stating this explicitly, that this condition is satisfied. If either $ u $ or $ v $ is fixed, the equations (3) define curves on the surface. Such curves are said to be coordinate lines on the surface. The parameters $ u $ and $ v $ are called surface coordinates or curvilinear Gaussian coordinates.

The concept of a tangent plane to a surface is defined in terms of the concept of contact. It is a plane passing through a point on the surface having contact of order $ \alpha \geq 1 $ with the surface at that point. A smooth (differentiable) surface has a unique tangent plane at each (regular) point. The tangent plane of a surface defined by equations (3), under condition (4) at the point $ ( u _ {0} , v _ {0} ) $, is defined by the equation

$$ \left | \begin{array}{ccc} {X - x ^ {0} } &{Y - y ^ {0} } &{Z - z ^ {0} } \\ {x _ {u} ^ {0} } &{y _ {u} ^ {0} } &{z _ {u} ^ {0} } \\ {x _ {v} ^ {0} } &{y _ {v} ^ {0} } &{z _ {v} ^ {0} } \\ \end{array} \right | = 0 , $$

where the superscript 0 indicates that the functions $ x ( u , v ) , y ( u , v ) , z ( u , v ) $ and their derivatives are evaluated at the point $ ( u _ {0} , v _ {0} ) $. The straight line which passes through a point of the surface and is perpendicular to the tangent plane at this point is called the normal to the surface. If $ \mathbf r ( u , v ) $ is a vector with coordinates $ x ( u , v ) , y ( u , v ) , z ( u , v ) $, then

$$ \mathbf r _ {u} \times \mathbf r _ {v} $$

has the direction of the normal to the surface.

The important concept of an osculating paraboloid is introduced for surfaces. This is a paraboloid the axis of which is the normal to the surface at the given point and with contact of order $ \alpha \geq 2 $ to the surface at this point. A twice differentiable surface has a unique osculating paraboloid at each of its points, which may degenerate to a parabolic cylinder or a plane. If the surface is described in Cartesian coordinates, with the given point as the coordinate origin, while the tangent plane at this point is taken as the $ xy $- plane, the equation of the surface in a neighbourhood of this point will be

$$ z = f ( x , y ) , $$

while the equation of the osculating paraboloid at this point is

$$ z = \frac{1}{2} ( f _ {xx} x ^ {2} + 2f _ {xy} xy + f _ {yy} y ^ {2} ) $$

(the derivatives of the function $ f $ being taken at the point of contact). Depending on the type of the osculating paraboloid, the points of the surface are divided into elliptic points, hyperbolic points, parabolic points, and flat points (cf. Elliptic point; Flat point; Hyperbolic point; Parabolic point). The importance of the osculating paraboloid is due to the fact that it reproduces the form of the surface up to infinitesimals of the second order (the tangent plane reproduces this form up to infinitesimals of the first order).

The osculating paraboloid is used to introduce the concept of conjugate directions on a surface. Namely, two directions on a surface at a given point are said to be conjugate if the straight lines generated by these directions are conjugate with respect to the osculating paraboloid at this point. Orthogonal conjugate directions are called principal. At a given point on the surface there are, as a rule, two principal directions. Flat points and special elliptic points (cf. Umbilical point), at which all directions are principal, form an exception to this rule. A curve on a surface for which the tangent direction is principal at all points is said to be a curvature line. At non-elliptic points of the surface there exist self-conjugate directions. They are known as asymptotic directions (cf. Asymptotic direction). A curve on a surface for which the direction is asymptotic at all points is known as an asymptotic line.

The concept of the envelope of a family of surfaces is introduced similarly to that of the envelope of a family of curves in a plane. However, the family of surfaces may be a one-parameter or a two-parameter family. In the theory of surfaces, the envelope of a one-parameter family of planes is of special significance.

An important role in the theory of surfaces is played by two differential quadratic forms, the fundamental forms of a surface. Let $ \mathbf r ( u , v ) $ denote the vector of a point on a surface, and let $ \mathbf n ( u , v ) $ denote the unit vector of the normal to the surface; the fundamental forms are then written as

$$ \textrm{ I } = d \mathbf r ^ {2} ,\ \textrm{ II } = - d \mathbf r d \mathbf n . $$

The coefficients of the first and the second fundamental form are usually denoted by $ E , F , G $ and $ L , M , N $, respectively. The first fundamental form yields the distance on the surface between a point $ ( u , v ) $ and an infinitesimally close point $ ( u + du , v + dv ) $:

$$ ds = \sqrt {E du ^ {2} + 2F du dv + G dv ^ {2} } . $$

The length of a curve defined on the surface by the equations $ u= u ( t) , v = v ( t) $ is computed with the aid of the first fundamental form:

$$ L = \int\limits _ {t _ {0} } ^ { t } \sqrt {E {u } ^ \prime 2 + 2F u ^ \prime v ^ \prime + G {v } ^ \prime 2 } dt . $$

The first fundamental form of the surface defines the angles between curves on the surface. In particular: the formula

$$ \cos \theta = \frac{F}{\sqrt {E G } } $$

is valid for the angle $ \theta $ between the coordinate lines $ u = \textrm{ const } , v = \textrm{ const } $ at a point where they intersect. It is seen, accordingly, that the coordinate net on the surface is orthogonal if $ F = 0 $. The area of a piece of the surface is also given by the first fundamental form and, for a domain $ \Omega $ on the surface, is computed by the formula

$$ S = {\int\limits \int\limits } _ \Omega \sqrt {EG - F ^ {2} } du dv . $$

The second fundamental form characterizes the twist of the surface in space. In fact, the ratio of the second to the first fundamental form,

$$ k = \frac{L du ^ {2} + 2M du dv + N dv ^ {2} }{E du ^ {2} + 2F du dv + G dv ^ {2} } , $$

represents the curvature of the planar section normal to the surface, drawn in the direction $ du : dv $( cf. Normal curvature of a surface). There is a simple connection between the curvature of a curve lying on the surface and the curvature of the normal section of the surface through the tangent of the curve (the Meusnier theorem). The extremal values of the normal curvature of a surface at a given point are known as the principal curvatures (cf. Principal curvature), and are reached in the principal directions. The normal curvature of a surface in an arbitrary direction can be expressed in terms of the principal curvatures and the angles formed by this direction with the principal directions (the Euler formula). The principal curvatures $ k _ {1} $ and $ k _ {2} $ are defined by the equation

$$ \left | \begin{array}{lr} Ek - L &Fk - M \\ Fk - M &Gk - N \\ \end{array} \right | = 0 . $$

Their mean value is known as the mean curvature of the surface. An important class of surfaces is constituted by surfaces of mean curvature zero — the so-called minimal surfaces (cf. Minimal surface). They are distinguished by the fact that a sufficiently small piece of such a surface has least area among all surfaces with the same boundary. The product $ K = k _ {1} k _ {2} $ of the principal curvatures is known as the Gaussian curvature of the surface:

$$ K = \frac{LN - M ^ {2} }{EG - F ^ {2} } . $$

It is seen from this formula that the Gaussian curvature of a surface can be expressed in terms of the coefficients of the first and second fundamental forms. However, the Gaussian curvature can be expressed in terms of the coefficients and their derivatives of the first form alone (the Gauss theorem).

Two surfaces between which it is possible to establish a homeomorphism preserving lengths of curves are called isometric surfaces.

The coefficients of the first and the second fundamental form are not independent. One relation between these coefficients is given by Gauss theorem. Two more relations have been discovered by K.M. Peterson and D. Codazzi (cf. Peterson–Codazzi equations). These three relations constitute a complete system of independent relations between the coefficients of the first and second fundamental forms of a surface. According to the Bonnet theorem, if the equations of Gauss, Peterson and Codazzi are satisfied for two differential fundamental forms the first one of which is positive definite, then there exists a surface, which is unique up to its location in space, with these forms as the first and second fundamental forms.

The branch of the theory of surfaces dealing with the properties of figures on the surface which depend on a measurement of the lengths of curves on the surface alone is known as the interior geometry of surfaces. Since the lengths of curves are determined by the first fundamental form, the properties concerned are connected with that form only. In particular, the objects of the interior geometry of surfaces are the lengths of curves, the angles between curves, the areas of domains, and the Gaussian curvature. An important concept in the interior geometry of surfaces is the concept of a geodesic line. This is the name given to a curve which, over a sufficiently small part of the surface, is the shortest among all curves on the surface connecting the end points of this segment. The next important concept in the interior geometry of surfaces is that of the geodesic curvature of a curve. The Gauss–Bonnet theorem relates the integral of the Gaussian curvature of a surface over a domain, the integral of the geodesic curvature over its boundary and the Euler characteristic.

The interior geometry of surfaces may be constructed as the geometry of a two-dimensional metric manifold in which the distance between two points $ ( u, v) $ and $ ( u+ du, v+ dv) $ which are infinitesimally close to each other is determined with the aid of a given differential form $ ds ^ {2} $. If this approach to the interior geometry of surfaces is adopted, it can be naturally extended: the given manifold has arbitrary dimension $ n $, while the metric is specified by a positive-definite differential quadratic form in $ n $ variables, $ ds ^ {2} = g _ {\alpha \beta } du ^ \alpha du ^ \beta $. In a further generalization, the form $ ds ^ {2} $ need not be positive definite. This leads to the theory of spaces of interest in the general theory of relativity, in particular, to Minkowski spaces (cf. Minkowski space). Finally, if the quadratic form $ ds ^ {2} $ is replaced by a general positive homogeneous form of the first degree in $ du ^ \alpha $, one obtains a Finsler space. An even further-going generalization of the interior geometry of surfaces is the geometry of spaces with connections with respect to a given group, in particular the geometry of spaces with an affine connection, a projective connection and a conformal connection.

References

[1]	L. Bianchi, "Lezioni di geometria differenziale" , 1–2 , Zanichelli , Bologna (1923–1927) Zbl 53.0659.03 Zbl 50.0454.03 Zbl 49.0498.06 Zbl 48.0784.02 Zbl 40.0658.02 Zbl 34.0670.01 Zbl 33.0633.01 Zbl 25.1165.01 Zbl 18.0648.01
[2]	G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1 , Gauthier-Villars (1887)
[3]	D.J. Struik, "A concise history of mathematics" , 1–2 , Dover, reprint (1948) (Translated from Dutch) MR0026572 Zbl 0032.09701
[4]	P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian)
[5]	A.V. Pogorelov, "Differential geometry" , Noordhoff (1959) (Translated from Russian) MR0114163 Zbl 0084.17702
[6]	W. Blaschke, "Einführung in die Differentialgeometrie" , Springer (1950) MR0043502 Zbl 0041.28804
[7]	W. Blaschke, "Vorlesungen über Differentialgeometrie und geometrische Grundlagen von Einsteins Relativitätstheorie. Elementare Differentialgeometrie" , 1 , Springer (1921) MR0015247
[8]	S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) MR0193578 Zbl 0129.13102
[9]	V.F. Kagan, "Foundations of the theory of surfaces in a tensor setting" , 1–2 , Moscow-Leningrad (1947–1948) (In Russian)
[10]	V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian)
[11]	J.A. Schouten, D.J. Struik, "Einführung in die neueren Methoden der Differentialgeometrie" , 2 , Noordhoff (1935) Zbl 0011.17404 Zbl 61.0784.01
[12]	S.P. Finikov, "Projective differential geometry" , Moscow-Leningrad (1937) (In Russian)
[13]	S.P. Finikov, "Theorie der Kongruenzen" , Akademie Verlag (1959) (Translated from Russian) MR0106480
[14]	P.A. Shirokov, A.P. Shirokov, "Differentialgeometrie" , Teubner (1962) (Translated from Russian) Zbl 0002.35103
[15]	A.P. Norden, "Spaces with an affine connection" , Nauka , Moscow-Leningrad (1976) (In Russian)

Comments

The main article above is concerned only with the differential geometry of curves and surfaces in two- or three-dimensional Euclidean space (see also Curve; Surface). Nowadays, in Western literature the phrase "differential geometry" refers also to the study of differentiable manifolds (cf. Differentiable manifold; Differential geometry of manifolds) and the various structures (Riemannian, Lorentzian, complex, projective, affine, etc.) that one can endow them with (cf., e.g., Riemannian manifold; Riemannian geometry; Complex manifold; Projective differential geometry; Finsler geometry; Affine differential geometry).

The Peterson–Codazzi equations are better known as the Mainardi–Codazzi equations.

Instead of interior geometry of surfaces the phrase intrinsic geometry of surfaces is often used.

Riemann's course can be found in [a12].

Consider a differentiable simple regular closed curve in the plane. If the curvature $ k $ is everywhere $ > 0 $ the curve is called a (generalized) oval. A vertex of such a planar curve is a point at which $ k $ has a relative maximum or minimum. The four-vertex theorem (Vierscheitelsatz) says that an oval has at least four vertices.

References

[a1]	M. Spivak, "A comprehensive introduction to differential geometry" , 1979 , Publish or Perish pp. 1–5 MR0532834 MR0532833 MR0532832 MR0532831 MR0532830 MR0394453 MR0394452 MR0372756 MR1537051 MR0271845 MR0267467 Zbl 1213.53001 Zbl 0439.53005 Zbl 0439.53004 Zbl 0439.53003 Zbl 0439.53002 Zbl 0439.53001 Zbl 0306.53003 Zbl 0306.53002 Zbl 0306.53001 Zbl 0202.52201 Zbl 0202.52001
[a2]	S.-S. Chern (ed.) , Studies in global geometry and analysis , Prentice-Hall (1967) MR0210537 Zbl 0175.48102
[a3]	D.J. Struik, "Lectures on classical differential geometry" , Addison-Wesley (1961) MR0939369 MR1528072 MR0036551 Zbl 0105.14707
[a4]	N.J. Hicks, "Notes on differential geometry" , v. Nostrand (1965) MR0179691 Zbl 0132.15104
[a5]	C.C. Hsiung, "A first course in differential geometry" , Wiley (Interscience) (1981)
[a6]	B. O'Neill, "Elementary differential geometry" , Acad. Press (1966) Zbl 0971.53500 Zbl 0974.53001
[a7]	M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) MR0917479 Zbl 0629.53001
[a8]	S. Kobayashi, K. Nomizu, "Foundations of differential geometry" , 1–2 , Interscience (1969) MR0238225 Zbl 0175.48504
[a9]	M. DoCarmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) Zbl 0326.53001
[a10]	J.A. Thorpe, "Elementary topics in differential geometry" , Springer (1979) MR0528129 Zbl 0404.53001
[a11]	W. Blaschke, K. Leichtweiss, "Elementare Differentialgeometrie" , Springer (1973) MR0350630 Zbl 0264.53001
[a12]	B. Riemann, "Ueber die Hypothesen, welche der Geometrie zuGrunde liegen" , Das Kontinuum und andere Monographien , Chelsea, reprint (1973) Zbl 0093.00101 Zbl 0087.35001 Zbl 47.0518.05

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️