Minimal surface
A surface for which the mean curvature $ H $
is zero at all points.
The first research on minimal surfaces goes back to J.L. Lagrange (1768), who considered the following variational problem: Find a surface of least area stretched across a given closed contour. Assuming that the required surface is given in the form $ z = z ( x , y) $, Lagrange showed that $ z ( x , y ) $ must satisfy the so-called Euler–Lagrange equation
$$ \tag{1 } ( 1 + q ^ {2} ) \frac{\partial ^ {2} z }{\partial x ^ {2} } - 2 p q \frac{\partial ^ {2} z }{\partial x \partial y } + ( 1 + p ^ {2} ) \frac{\partial ^ {2} z }{\partial y ^ {2} } = 0 , $$
$$ p = \frac{\partial z }{\partial x } ,\ q = \frac{\partial z }{\partial y } . $$
Later G. Monge (1776) discovered that the condition for minimality of a surface leads to the condition $ H = 0 $, and therefore surfaces with $ H = 0 $ are called "minimal" . In reality, however, it is necessary to distinguish the notions of a minimal surface and a surface of least area, since the condition $ H = 0 $ is only a necessary condition for minimality of area, which follows from the vanishing of the first variation of the surface area among all surfaces of class $ C ^ {2} $ with the given boundary. To verify that in this class even a relative (local) minimum is attained, it is necessary to investigate the second variation of the surface area.
The theory of minimal surfaces has a rich history; it was taken up by almost-all prominent mathematicians of the 19th century and 20th century. Its problems stimulated the development of many neighbouring domains of mathematics. The first general method of integration of the Euler–Lagrange equations was suggested by Monge (1784) and A. Legendre (1787) in the form of the so-called Monge formula, obtained from the complex characteristic of (1):
$$ x = A ( t) + A _ {1} ( \tau ) ,\ y = B ( t) + B _ {1} ( \tau ) ,\ \ z = C ( t) + C _ {1} ( \tau ) , $$
where $ t $ and $ \tau $ are complex variables and $ A ( t) \dots C _ {1} ( \tau ) $ are holomorphic functions satisfying the conditions
$$ A ^ { \prime 2 } ( t) + B ^ { \prime 2 } ( t) + C ^ { \prime 2 } ( t) = 0 ,\ \ A _ {1} ^ { \prime 2 } ( \tau ) + B _ {1} ^ { \prime 2 } ( \tau ) + C _ {1} ^ { \prime 2 } ( \tau ) = 0. $$
However, these methods, by virtue of the insufficient development of complex function theory at that time, remained without application for a long time. (In 1832 S. Poisson wrote that it is difficult to derive any benefit from Monge's formula since it had been complicated by the introduction of complex variables.)
New results on minimal surfaces began to appear only from the beginning of the 1830's. Poisson announced (1832) his solution of the Lagrange variational problem when the boundary of the surface is near to a plane curve. Shortly afterwards a third minimal surface, the Scherk surface (H. Scherk, 1834), was added to the already known minimal surfaces: the catenoid (L. Euler, 1774, J. Meusnier, 1776) and the helicoid (Meusnier, 1776). In 1842 E. Catalan proved that the helicoid is the unique ruled minimal surface; in 1844 the Björling problem was raised and solved; in the 1850's, in a series of papers, O. Bonnet gave new proofs of the facts known at that time on the theory of minimal surfaces and found other properties of minimal surfaces (the uniqueness of the catenoid as a minimal surface of revolution, the conformality of spherical Gauss mappings of minimal surfaces (cf. also Spherical map), etc.).
In 1866 the Weierstrass formula was discovered:
$$ x = x _ {0} + \mathop{\rm Re} \int\limits _ { 0 } ^ { w } ( f ^ { 2 } - g ^ {2} ) dw , $$
$$ y = y _ {0} + \mathop{\rm Re} \int\limits _ { 0 } ^ { w } i ( f ^ { 2 } + g ^ {2} ) dw , $$
$$ z = z _ {0} + 2 \mathop{\rm Re} \int\limits _ { 0 } ^ { w } f g dw , $$
representing a simply-connected minimal surface $ S ( x , y , z ) $ by holomorphic functions $ f ( w) $ and $ g ( w) $, defined in the disc or in the whole plane of variation of the intrinsic isothermal coordinates $ ( u , v ) $, $ w = u + iv $. These formulas are equivalent to, or contain as particular cases, all the other then known parametric representations of minimal surfaces (B. Riemann (1860), A. Enneper (1864), K.M. Peterson (1866), and others) and give a regular minimal surface if and only if $ f $ and $ g $ do not have common zeros. In the case of common zeros of $ f $ and $ g $, the surface is a so-called generalized minimal surface with a degenerate metric at the common zeros of $ f $ and $ g $:
$$ d s ^ {2} = ( | f | ^ {2} + | g | ^ {2} ) ( d u ^ {2} + d v ^ {2} ) . $$
At such a point, a branching point (cf. Branching point (of a minimal surface)) of the minimal surface appears. Using the Weierstrass formula it became possible to explicitly construct and study many concrete minimal surfaces; in particular, algebraic minimal surfaces are obtained for algebraic functions $ f $ and $ g $.
In 1874 H.A. Schwarz obtained a representation of a minimal surface in isothermal coordinates $ ( u , v ) $ in the form
$$ r ( w) = r ( u + iv ) = \mathop{\rm Re} \left [ F ( w) - i \int\limits _ { 0 } ^ { w } n ( w ) dF ( w ) \right ] , $$
where $ F ( w) $ and $ n ( w) $ are three-dimensional vectors with holomorphic coordinates, coinciding respectively with $ r ( u , 0 ) $ and the unit normal $ n ( u , 0 ) $ to the minimal surface. For $ \mathop{\rm Im} w = 0 $ this formula gives an explicit solution to the Björling problem and allows the extension to minimal surfaces of the Schwarz symmetry principle.
In the same decade S. Lie (1878) developed his interpretation of the Monge formula, assigning to each minimal surface with a harmonic radius vector $ r ( w) $ a complex-analytic curve:
$$ z = R ( w) \in C ^ {3} ,\ \mathop{\rm Re} R ( w) = \frac{1}{2} r ( w), $$
and representing the minimal surface as a translation surface of the curve $ R ( w) $ and its complex conjugate curve $ \overline{ {R ( w) }}\; $; this served as a starting point for the establishment of a fruitful connection between minimal surfaces and analytic curves. Thus, the work of K. Weierstrass, Lie, Riemann, Schwarz, and others resulted, at the end of the 19th century, in the wide use of methods and results of complex function theory in the theory of minimal surfaces.
In his experiments J. Plateau (1849) arrived at the physical realization of minimal surfaces in the form of soap films, stretched on wire frames of various shapes. His experiments revived the interest in the old problem of finding minimal surfaces with a given boundary contour. This problem came to be called the Plateau problem. The first solution of it was obtained for various polygonal contours; in this connection, in particular, the Riemann–Schwarz surface was discovered.
In 1816, in the theory of minimal surfaces there appeared the novel Gergonne problem: To find a minimal surface if part of its boundary is given and the remainder is situated in some preassigned surface; this problem came to be called the problem on a minimal surface with free boundary. The first results towards its solution also related to cases when the given part of the boundary consists of line segments and the remainder lies in given planes (for more details see [1], [2]).
At the beginning of the 20th century there was an intensified interest in the study of minimal surfaces "in the large" . The Dirichlet problem for the Euler–Lagrange equation was studied (A. Korn (1909), S.N. Bernshtein (1910)) and Bernshtein proved his theorem on minimal surfaces (1916, cf. also Bernstein theorem); in general, starting with Bernshtein's work on the theory of minimal surfaces, methods of the theory of partial differential equations came to be used. H. Liebmann (1919) established a connection between minimal surfaces and infinitesimal deformations of spheres. The crowning achievement of the first half of the 20th century in the theory of minimal surfaces was the complete solution of Plateau's problem, initially for simply-connected surfaces, and then for two-dimensional surfaces of arbitrary topological type in a Euclidean or a Riemannian space (see [1]–[5]). The results on minimal surfaces were extended to the case of more general variational problems (generalizing the variational problems for a minimal surface), more general differential equations (generalizing the Euler–Lagrange equations for a minimal surface) and to a more general class of surfaces (for example, with constant mean curvature) (see [3], [6], [7]).
From the available results and the leading research on minimal surfaces several directions can be selected.
1) The intrinsic geometry of minimal surfaces. Not every Riemannian manifold of non-positive curvature can be isometrically immersed in a Euclidean space $ E ^ {n} $, $ n \geq 3 $, as a minimal surface. The criterion for the existence of a minimal surface in $ E ^ {3} $ with a given metric is given in the following theorem of Ricci: For a given metric $ ds ^ {2} $ to be isometric to the metric of some minimal surface in $ E ^ {3} $ it is necessary and sufficient that its curvature $ K $ be non-positive and that at the points where $ K < 0 $ the metric $ d \sigma ^ {2} = \sqrt {- K } ds ^ {2} $ be Euclidean.
There is also a necessary and sufficient condition that a given two-dimensional metric be the metric of a minimal surface in a Euclidean space $ E ^ {n} $, $ n > 3 $. In particular, a metric with the Ricci condition (i.e. satisfying the conditions of Ricci's theorem) can be the metric of a minimal surface only in $ E ^ {3} $ or $ E ^ {6} $, and there is also a complete description of all minimal surfaces with the same metric: they make up a so-called associated family of isometric minimal surfaces; for instance, in $ E ^ {3} $ all minimal surfaces isometric to a given minimal surface $ F $ with $ X _ {k} = \mathop{\rm Re} \Phi _ {k} ( w) $, $ w = u + i v $, where $ ( u , v ) $ are isothermal coordinates, $ \Phi _ {k} ( w) $ is a holomorphic function and $ 1 \leq k \leq 3 $, form the family of associated minimal surfaces $ F _ \alpha $ with $ x _ {k} = \mathop{\rm Re} ( \Phi _ {k} ( w) e ^ {- i d } ) $, $ F _ {0} = F $. So the catenoid and helicoid are two associated (hence isometric) minimal surfaces, with parameters $ \alpha = 0 $ and $ \alpha = \pi / 2 $. In the problem of immersion as a minimal surface of a metric $ d s ^ {2} $ in a Euclidean space $ E ^ {n} $, $ n > 3 $, one can indicate lower and upper bounds on $ n $ using a generalized Ricci condition. Moreover, in terms of certain classes of holomorphic mappings this problem has a complete solution. There is also a number of results on the intrinsic nature of the metrics of two-dimensional minimal surfaces in a sphere $ S ^ {n} $, $ n \geq 3 $( see ). For the metrics of multi-dimensional minimal surfaces a necessary and sufficient condition is known only in the case of hypersurfaces [16]. Isometric deformations of minimal surfaces into a surface of another extrinsic structure have also not been very much studied, not even for $ E ^ {3} $.
Another circle of problems in the intrinsic geometry of minimal surfaces is formed by isoperimetric inequalities (cf. Isoperimetric inequality; Isoperimetric inequality, classical), which, however, in their most exact and interesting forms depend on the exterior structure of the minimal surface (see [9]).
2) Local properties of minimal surfaces. Here one may mention results on the analyticity of minimal surfaces (the definition of a minimal surface requires only that it be of class $ C ^ {2} $) and the solution of a number of variational problems, the result that a sufficiently small domain of a minimal surface realizes absolutely minimal area among all surfaces with the same boundary as the domain in question, theorems on the removability of isolated or low-order singularities of the solutions of the equations of a minimal surface and their generalizations, the study of the structure of generalized minimal surfaces in a neighbourhood of branching points, research on singularities of minimal surfaces, and the solution of so-called elliptic variational problems in multi-dimensional Euclidean and Riemannian spaces (see [2], [3], [6], [10], [12]).
3) The study of concrete minimal surfaces or of minimal surfaces with preassigned boundary properties, plane sections, spherical Gauss mappings, etc. For example, the theorem on the convexity of the horizontal sections of doubly-connected minimal surfaces with convex horizontal boundaries; the theorem on the coincidence with the catenoid of a complete minimal surface situated between two planes $ z = C _ {1} $ and $ z = C _ {2} $, $ - \infty \leq C _ {1} < C _ {2} \leq \infty $, and having star-shaped sections $ z = \textrm{ const } $, the detailed study of the classical minimal surfaces of Enneper, Scherk, Riemann–Schwarz and others. Special mention must be given to the research on minimal cones in $ \mathbf R ^ {n} $, $ n \geq 4 $, leading to the construction of a counter-example to Bernstein's theorem in $ E ^ {n} $, $ n \geq 9 $, and to the finding of an example of an irregular solution of the Plateau problem for hyperplanes in $ E ^ {8} $. Concrete examples of various minimal surfaces have also begun to be studied in multi-dimensional Riemannian spaces (see [1], [2], [6], [12], [13]).
4) The development of the theory of minimal surfaces in $ E ^ {n} $, $ n \geq 3 $, by analogy with functions of a complex variable in $ \mathbf C ^ {1} $. Here one may mention results on boundary properties of minimal surfaces, the theorem on the analytic continuation of minimal surfaces across regular arcs of the boundary, theorems on the smoothness of a minimal surface in dependence on the smoothness of its boundary (for example, if the boundary is of class $ C ^ {n , \alpha } $, $ n \geq 1 $, $ 0 < \alpha < 1 $, then the minimal surface is of the same class), and work on the construction for minimal surfaces of an analogue of Nevanlinna value-distribution theory for meromorphic functions (see [2], [6], [13], [15]).
5) Work on the Euler–Lagrange theorem. Side-by-side with the study "in the large" of solutions of this equation and its generalization for $ n $- dimensional minimal surfaces $ ( x _ {1} \dots x _ {n} , f _ {1} ( x) \dots f _ {k} ( x) ) $ in $ E ^ {n+} k $, $ k \geq 1 $,
$$ \tag{2 } \sum _ {i , j = 1 } ^ { n } g ^ {ij} \frac{\partial ^ {2} f }{\partial x ^ {i} \partial x ^ {j} } = 0 $$
(where $ f = ( f _ {1} \dots f _ {k} ) $ and $ g ^ {ij} $ are the contravariant components of the metric tensor $ g _ {ij} $), a large amount of work has been devoted to the local behaviour of the solutions of the Euler–Lagrange equation and its generalization (2). There are the questions on the removability of singularities for codimension $ k = 1 $, the existence of irregular solutions for large codimension, and, particularly, the investigation of the Dirichlet problem. This problem can be treated in another way as the Plateau problem of determining a minimal surface with given contour and with the additional condition of single-valued projection of the minimal surface into the plane containing the boundary contour. Such a treatment, in many cases, allows one to obtain a conclusion of the Dirichlet problem on the basis of known results on the Plateau problem (for example, the existence and uniqueness of the solution of the Dirichlet problem in $ E ^ {3} $ for a convex domain $ D $ is a corollary of Radó's theorem on the Plateau problem).
In the general case it has been established that for the solvability of the Dirichlet problem in codimension 1 for any continuous boundary function, it is necessary and sufficient that the mean curvature vector of the boundary $ \partial D $ is directed into the domain $ D $( for $ n = 2 $ this means that $ D $ is convex); here the solution of the problem is also unique. Regarding non-convex domains it has been proved, e.g., that for any non-convex domain $ D $ with Jordan boundary $ \partial D $ it is possible to find a continuous function $ \phi ( p ) $, $ p \in \partial D $, such that the corresponding Dirichlet problem is unsolvable. In large codimensions the Dirichlet problem is unsolvable even when the domain is a ball in $ E ^ {n} $.
The Dirichlet problem has also been discussed in the exterior of $ D $. Here, new facts have been obtained (for example, uniqueness of the solution is lost, solvability is not obtained everywhere, etc.). There are also results on the Dirichlet problem with incomplete or partially unbounded boundary values (see [2], [6]–, [14]).
6) Complete minimal surfaces. By complete minimal surfaces are meant minimal surfaces which are complete as metric spaces relative to their intrinsic metric (cf. Internal metric). Complete minimal surfaces may be compact (without boundary) and non-compact, or open. In research on complete minimal surfaces interest is basically directed to the study of connections between the global metric, geometric and topological properties of the surfaces.
Most progress has been made in the study of two-dimensional complete minimal surfaces in $ E ^ {n} $, $ n \geq 3 $, where most of the results have been obtained by applying methods of complex function theory. In particular, it has been shown that there is a complete minimal surface in $ E ^ {3} $ of any preassigned genus $ g $ and connectivity $ k $; theorems have been obtained on the relations between the integral of the curvature, $ \int \int K d S $, and the topological and conformal types of a complete minimal surface (for example, $ \int \int K d S \leq 2 \pi ( \chi - k ) $, where $ \chi $ is the Euler characteristic of the surface and $ k $ is the number of components of the boundary; if $ | \int \int K d S | < \infty $, then the surface $ S $ is conformally equivalent to a Riemann sphere with a finite number of punctured points; if a complete minimal surface $ S $ is infinitely connected or of conformally hyperbolic type, then its total curvature is infinite and the normals to $ S $ attain all directions an infinite number of times, with the possible exception of a set of directions of capacity zero, etc.). The structure of spherical Gauss mappings has been studied (for example, a complete minimal surface in $ E ^ {3} $ is either a plane or its spherical image does not contain a set of capacity zero, a complete minimal surface in $ E ^ {n} $, $ n \geq 3 $, is either a plane or its image under a generalized spherical Gauss mapping intersects an everywhere-dense set of hyperplanes, for any $ n \leq 4 $ there exist complete minimal surfaces in $ E ^ {3} $ whose spherical images do not contain precisely $ n $ preassigned points, etc.); surfaces have been found which are completely determined by their total curvature and topological type (these are the catenoid and the Enneper surface); the exterior unboundedness in $ E ^ {n} $, $ n \geq 3 $, of a complete minimal surface with bounded total curvature has been shown (see the references in [2], , [18], [21]).
Results on compact minimal surfaces are, on the whole, concerned with complete minimal surfaces situated in spheres $ S ^ {n} \subset E ^ {n+} 1 $. The interest in these minimal surfaces is explained, apart from the difficulties in the case of a general Riemannian space, by the presence of important relationships between minimal cones in $ E ^ {n+} 1 $ and minimal surfaces in $ S ^ {n} $( each hypercone in $ E ^ {n+} 1 $, definable by its vertex 0 and its intersection with a sphere $ S ^ {n} $ with centre at $ 0 $, is minimal if and only if its intersection with $ S ^ {n} $ is a minimal surface in $ S ^ {n} $). The questions analyzed here are, on the whole, the same as for complete minimal surfaces in $ E ^ {n} $. For example, it has been shown that any compact two-dimensional manifold, with the exception of the projective plane, can be realized as a complete minimal surface in $ S ^ {3} $; in $ S ^ {3} $ an analogue of Bernstein's theorem has been obtained: If the normals to a complete minimal surface lie in an open hemisphere, then the minimal surface is the equatorial hypersphere; other criteria have been found for a complete minimal surface in $ S ^ {n} $ to be a hypersphere; the possible forms and the questions of uniqueness of complete minimal surfaces in $ S ^ {n} $, in dependence on the value of their scalar curvature, have been investigated, etc. (see [2], [6], , [13]).
7) The construction of a different kind of generalized minimal surface, and also of equations and variational problems the solutions of which preserve the properties of a minimal surface. Here the classical theory of minimal surfaces is directly bordering on work about surfaces with given mean curvature, about quasi-conformal spherical Gauss mappings, and on work about quasi-linear elliptic equations with many of the properties of the Euler–Lagrange equation in two or more variables. More remote generalizations have been made in theories connecting minimal surfaces with sets which minimize integral flows or various Hausdorff measures, etc. (see [2], [6], [7], [10], [11]).
8) Work on the Plateau problem for two-dimensional and multi-dimensional minimal surfaces (see Plateau problem; Plateau problem, multi-dimensional).
From this list of problems and results it is clear that the range of questions in the theory of minimal surfaces is very large, and correspondingly diverse are the methods applied in them. In classical investigations, on the whole, the methods of differential geometry, complex function theory and differential equations were applied, whereas now there is a growing use of the methods of topology, measure theory and functional analysis, particularly in research on minimal surfaces in multi-dimensional spaces.
Since the time of publication and, especially, preparation of this article, important progress has been made in all questions mentioned above, see [18]–[22]; in addition one could mention the development of computer-aided investigations on minimal surfaces; see, e.g., [17].
References
| [1] | R. Courant, "Dirichlet's principle, conformal mapping, and minimal surfaces" , Interscience (1950) (With appendix by M. Schiffer: Some recent developments in the theory of conformal mapping) MR36317 |
| [2] | J.C.C. Nitsche, "Vorlesungen über Minimalflächen" , Springer (1975) MR0448224 Zbl 0319.53003 |
| [3] | T. Radó, "On the problem of Plateau" , Chelsea, reprint (1951) MR0040601 Zbl 0211.13803 Zbl 0007.11804 Zbl 59.1341.01 Zbl 57.0605.11 Zbl 56.0437.01 |
| [4] | J. Douglas, "Solution of the problem of Plateau" Trans. Amer. Math. Soc. , 33 (1931) pp. 263–321 MR1501590 Zbl 0001.14102 Zbl 57.1542.03 Zbl 57.0605.07 Zbl 57.0601.01 |
| [5] | C. Morrey, "The problem of Plateau on a Riemannian manifold" Ann. of Math. , 49 (1948) pp. 807–851 MR0027137 Zbl 0033.39601 |
| [6] | J.C.C. Nitsche, "On new results in the theory of minimal surfaces" Bull. Amer. Math. Soc. , 71 (1965) pp. 195–270 MR0173993 Zbl 0135.21701 |
| [7] | R. Osserman, "A survey of minimal surfaces" , v. Nostrand-Reinhold (1969) MR0256278 Zbl 0209.52901 |
| [8a] | R. Osserman, "Minimal varieties" Bull. Amer. Math. Soc. , 75 (1969) pp. 1092–1120 MR0276875 Zbl 0188.53801 |
| [8b] | R. Osserman, "Global properties of minimal surfaces in 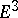 and and 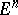 " Ann. of Math. (2) , 80 (1964) pp. 340–364 MR0179701 Zbl 0134.38502 " Ann. of Math. (2) , 80 (1964) pp. 340–364 MR0179701 Zbl 0134.38502 |
| [9] | R. Osserman, "The isoperimetric inequality" Bull. Amer. Math. Soc. , 84 (1978) pp. 1182–1238 MR0500557 Zbl 0411.52006 |
| [10] | H. Federer, "Geometric measure theory" , Springer (1969) MR0257325 Zbl 0176.00801 |
| [11] | C. Morrey, "Multiple integrals in the calculus of variations" , Springer (1966) MR0202511 Zbl 0142.38701 |
| [12] | A.T. Fomenko, "Minimal compacta in Riemannian manifolds and Reifenberg's conjecture" Math. USSR Izv. , 6 : 5 (1972) pp. 1037–1066 Izv. Akad. Nauk SSSR Ser. Mat. , 36 : 5 (1972) pp. 1049–1079 |
| [13] | H. Lawson, "Complete minimal surfaces in 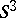 " Ann. of Math. , 92 (1970) pp. 335–374 MR0270280 Zbl 0205.52001 " Ann. of Math. , 92 (1970) pp. 335–374 MR0270280 Zbl 0205.52001 |
| [14] | H. Lawson, R. Osserman, "Non-existence, non-uniqueness and irregularity of solutions to the minimal surface system" Acta. Math. , 139 (1977) pp. 1–17 MR0452745 Zbl 0376.49016 |
| [15] | A.Ya. Vikaruk, "Analogs of Nevanlinna's theorems for minimal surfaces" Math. USSR Sb. , 29 : 4 (1976) pp. 497–520 Mat. Sb. , 100 : 4 (1976) pp. 555–579 |
| [16] | S.-S. Chern, R. Osserman, "Remarks on the Riemannian metric of a minimal submanifold" E. Looijenga (ed.) D. Siersma (ed.) F. Takens (ed.) , Geometry Symp. (Utrecht, 1980) , Lect. notes in math. , 894 , Springer (1981) pp. 49–90 MR0655419 Zbl 0477.53056 |
| [17] | D. Hoffman, "The computer-aided discovery of new embedded minimal surfaces" Math. Intell. , 9 : 3 (1987) pp. 8–21 MR0895770 Zbl 0616.53007 |
| [18] | W.H., III Meeus, "A survey of the geometric results in the classical theory of minimal surfaces" Bol. Soc. Brasil. Mat. , 12 : 1 (1981) pp. 29–86 |
| [19] | E. Bombieri (ed.) , Seminar of minimal submanifolds , Annals Math. Studies , 103 , Princeton Univ. Press (1983) MR795226 |
| [20] | S.-T. Yau, "Minimal surfaces and their role in differential geometry" T.J. Willmore (ed.) N.J. Hitchin (ed.) , Global Riemannian geometry , Horwood (1984) pp. 99–103 MR0757211 Zbl 0615.53053 |
| [21] | Dao Chong Tkhi, A.T. Fomenko, "Minimal surfaces and Plateau's problem" , Amer. Math. Soc. (Forthcoming) (Translated from Russian) |
| [22] | A.T. Fomenko, "Variational problems in topology" , Kluwer (1990) (Translated from Russian) MR1088735 Zbl 0716.53004 |
Minimal surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Minimal_surface&oldid=47844