Plateau problem, multi-dimensional
A term denoting a number of problems related to research on extremals and global minima of functionals in the $ k $-dimensional volume $ \mathop{\rm vol} _ {k} $
defined on $ k $-dimensional generalized surfaces that are imbedded in an $ n $-dimensional Riemannian space $ M ^ {n} $
and that satisfy certain boundary conditions.
In the history of this variational problem (see Plateau problem) one may distinguish several periods, characterized by different approaches to the concepts of a "surface" , a "boundary" and "minimization" , and, correspondingly, to methods of obtaining the minimal solution. The multi-dimensional Plateau problem is formulated as follows. Let $ A ^ {k-1 } \subset M ^ {n} $ be a fixed closed smooth $ ( k- 1) $-dimensional submanifold in a Riemannian space $ M ^ {n} $ and let $ X( A) $ be the class of all films (surfaces) $ X \subset M ^ {n} $ having $ A $ as boundary. Here, each film $ X \in X( A) $ allows a continuous parametrization (it can be represented as the transform of some manifold with boundary), i.e. $ f( W)= X $, where $ W $ is a certain $ k $-dimensional manifold with boundary $ \partial W $ homeomorphic to $ A $, while $ f: W\rightarrow M ^ {n} $ is a continuous mapping that coincides with a given homeomorphism at $ \partial W $, i.e. $ f: \partial W\rightarrow A $. The question is whether one can find in the class $ X( A) $ a film $ X _ {0} $ that would in some reasonable sense be minimal, i.e. such that its $ k $-dimensional volume is less than those of other films $ X $ of the same class. The transfer of classical "two-dimensional" methods to the multi-dimensional case encounters serious difficulties. E.g., the classical formulation of the multi-dimensional Plateau problem was set aside for some time and the problem was formulated in other (homological) terms. If one discards the concept of a manifold-film with boundary $ \partial W = A $ and extensively generalizes the concepts of a film and its boundary, while weakening the link between the two (in particular, if one considers non-parametrized films), and if one discards the condition $ X= f( W) $, then the multi-dimensional problem can be formulated in the language of the ordinary integer homology groups $ H _ {*} $: Find the minimal film $ X _ {0} $ that annihilates the fundamental cycle $ [ A] \in H _ {k-1} ( A) $ of a manifold $ A $( on the assumption that $ A $ can be oriented), i.e. $ i _ {*} [ A] = 0 $, $ i _ {*} : H _ {k-1} ( A) \rightarrow H _ {k-1} ( X) $, where $ i _ {*} $ is the homomorphism induced by the imbedding $ i: A\rightarrow X $. To solve the multi-dimensional problem in this new and extended formulation, a geometrical approach has been developed [1], [2], in which one minimizes a function of the $ k $-dimensional Hausdorff measure (volume) defined on $ k $-dimensional measurable compact sets (surfaces) in $ M ^ {n} $, and a theory has been developed [3], [4] of integral currents and varifolds with $ k $-rectifiable subsets in $ M ^ {n} $ as supports. In both directions fundamental theorems on the existence of minimal surfaces with a given boundary have been proved (E.R. Reifenberg, C.B. Morrey, H. Federer, W. Fleming, F.J. Almgren, E. de Giorgi, R. Harvey, H.B. Lawson, J. Simons, E. Giusti, and others). For a review on the tremendous literature on this question, see [1], [3], [4]. In particular, in the well-known work of Reifenberg the multi-dimensional Plateau problem has been solved in terms of spectral homology (Čech homology). It was also proved that a minimal surface, spanned over a "multi-dimensional" contour, is a manifold of corresponding smoothness class almost-everywhere, except at, possibly, a set of singular points of measure zero. Famous theorems on the existence of minimal surfaces in terms of minimal currents, minimal varifolds with a fixed boundary or without boundary, were proved by Federer, Fleming and Almgren [3], [4]. As in the previous case, the minimal surfaces turned out to be manifolds outside, possibly, a set of singular points of measure zero. Later the equivariant Plateau problem was solved by W.Y. Hsiang and Lawson [16]. More precisely, the existence of a minimal surface in a Euclidean space having the same symmetry groups on the multi-dimensional boundary "contour" has been proved. The transition of this theorem to arbitrary Riemannian manifolds was completed by J.E. Brothers [17]. The complex version of Plateau's problem was obtained by Harvey and Lawson . In particular, existence conditions for complex minimal films with a given boundary were discovered. Later, the "Lagrange variant" of the multi-dimensional Plateau problem was obtained by Harvey and Lawson [19]. As a result, minimality conditions for Lagrange submanifolds in the symplectic complex linear space $ \mathbf C ^ {n} $ were obtained. Deep results and existence theorems for minimal surfaces were obtained by S.-T. Yau [20]. He revealed the link between the existence of complex minimal surfaces and Kohn–Rossi cohomology. Using the theory of minimal surfaces, clear results were obtained by W.H. Meeks and Yau on the theory of three-dimensional manifolds, [21]. Note that if one has a theorem on the existence of a minimal solution in the homology class $ X( A) $, one can as before still say nothing on the existence of a minimal solution in the class of all films that are continuous transforms of manifolds with boundaries, i.e. that allow a parametrization. The fact is that if a manifold $ A $ is homologous to zero (as a cycle) in a film $ X _ {0} $, then $ X _ {0} $ does not necessarily have a representation in the form $ X _ {0} = f( W _ {0} ) $, where $ W _ {0} $ is some $ k $-dimensional manifold with boundary.
In [5], [6] a solution to a variant of the multi-dimensional Plateau problem was given in terms of spectral bordism. The spectral bordism groups are defined, for any compact space, using a Čech process analogous to the definition of spectral (Čech) homology. This process allows one to extend ordinary bordism groups of polyhedral classes and cell complexes to the wider class of compacta (e.g., in Riemannian manifolds). An element of a spectral bordism group can be represented by a sequence of manifolds, connected by mappings. For finite cell complexes this element is represented by one manifold (ordinary bordism). If a topological space is, e.g., a finite cell complex, then its spectral bordism group coincides with the ordinary singular bordisms. It was found that the classical problem has an equivalent formulation in the language of bordisms (cf. Bordism). Let $ V $ be a compact oriented closed $ ( k- 1) $-dimensional manifold and let $ f: V\rightarrow M ^ {n} $ be a continuous mapping; the pair $ ( V, f ) $ is called a singular bordism of $ M ^ {n} $. Two bordisms $ ( V _ {1} , f _ {1} ) $ and $ ( V _ {2} , f _ {2} ) $ are said to be equivalent if there exists a $ k $-dimensional oriented manifold $ W $ with boundary $ \partial W = V _ {1} \cup (- V _ {2} ) $ (where $ - V _ {2} $ denotes $ V _ {2} $ with the opposite orientation) and a continuous mapping $ F: W \rightarrow M ^ {n} $ such that $ F\mid _ {V _ {1} } = f _ {1} $, $ F\mid _ {V _ {2} } = f _ {2} $. The bordism $ ( V, f ) $ is equivalent to zero if $ V = \partial W = V _ {1} $, $ V _ {2} = \emptyset $. The equivalence classes of singular bordisms form an Abelian group, which after stabilization forms one of the generalized homology theories (bordism theory). The multi-dimensional Plateau problem is formulated (in this language) as follows: a) Can one find an $ X _ {0} $ with least volume $ \mathop{\rm vol} _ {k} X _ {0} $ among all films $ X \subset M $, $ A \subset X $, having the property that the singular bordism $ ( A, i) $ is equivalent to zero in $ X $, where $ i : A \rightarrow X $ is the imbedding? b) Can one find a bordism $ ( V _ {0} , g _ {0} ) $ among all singular bordisms $ ( V, g) $ equivalent to a given bordism $ ( V ^ { \prime } , g ^ \prime ) $( where $ g: V \rightarrow M ^ {n} $) such that the volume of the film $ g _ {0} ( X _ {0} ) \subset M ^ {n} $ is minimal?
The classical multi-dimensional Plateau problem differs considerably from the homological variant.
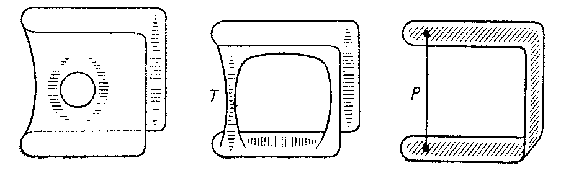
Figure: p072850a
Fig. a shows the contour $ A = S ^ {1} $ and the film $ X $ that tends to occupy a position in $ \mathbf R ^ {3} $ corresponding to minimal area. At a certain instant, the film links up and collapses, and instead of the two-dimensional tube $ T $ one gets a one-dimensional segment $ P $. In the two-dimensional case, the segment $ P $ may be mapped continuously into a two-dimensional disc glued to $ A $. In the multi-dimensional case, this effect of zones with fewer dimensions occurring in a minimal film is present to an even greater extent, and whereas all such parts $ P $, $ \mathop{\rm dim} P \leq k- 1 $, in the two-dimensional case can be mapped without loss of the parametrizing properties of $ X _ {0} $ into a $ k $-dimensional (two-dimensional) part of this film, for $ k> 2 $ these zones of fewer dimensions, in general, cannot be eliminated (if one wishes to retain the topological property of $ X _ {0} $ of annihilating the bordism $ ( A, i) $). For the same reasons, the zones of fewer dimensions cannot be discarded, since a $ k $-dimensional part $ X ^ {(k)} $ of a film $ X $ need not have a continuous parametrization, and thus, generally speaking, need not annihilate the bordism $ ( A, i) $. This shows that it is necessary to introduce the stratified volume of the film $ X $, composed of the volumes of all zones $ X ^ {(i)} $, i.e. $ \mathop{\rm vol} _ {k} X ^ {(k)} $, $ \mathop{\rm vol} _ {k-1} X ^ {(k- 1)} ,\dots $. A theorem representing a solution to a variant of the multi-dimensional Plateau problem in terms of spectral bordism is as follows [5], [6]: There exists a globally-minimal surface that minimizes the stratified volume.
Consequence: For any fixed oriented smooth closed $ ( k- 1) $-dimensional submanifold $ A $ in a Riemannian space $ M ^ {n} $ (in the case where $ X( A) \neq \emptyset $), there exists a globally-minimal surface $ X _ {0} $ that annihilates the spectral bordism $ ( A , i ) $. If the minimal film $ X _ {0} $ is a finite cell complex, it is representable in the form $ X _ {0} = f ( W _ {0} ) $, where $ W _ {0} $ is some manifold and $ f : W _ {0} \rightarrow M $ is a mapping that is a homeomorphism from the boundary $ \partial W _ {0} $ of $ W _ {0} $ onto the manifold $ A $, [5], . Also, the film $ X _ {0} $ is minimal in each of its dimensions $ \leq k $; if $ X ^ {(s)} $ is the part of $ X $ having dimension $ s $, then $ X ^ {(s)} $ contains a subset $ Z ^ {(s)} $ of $ s $-dimensional volume zero, while the complement $ X ^ {(s)} \setminus Z ^ {(s)} $ is an open $ s $-dimensional everywhere-dense analytic submanifold in $ M ^ {n} $. Here $ Z ^ {(s)} $ is the set of singular points in dimension $ s $.
This result is a particular case of a general theorem on the existence and almost-everywhere regularity of a globally-minimal surface, which has been proved [5], [6],
for any generalized (co)homology theory and for any set of boundary conditions. Also, such a surface exists in each stable homotopy class. The following is an example of a variational problem formulated and solved in cohomology terms. Let $ \xi $ be a stably non-trivial vector bundle on a compact Riemannian space $ M ^ {n} $; let $ X( \xi ) $ be the class of all surfaces $ X \subset M ^ {n} $ such that the restriction $ \xi \mid _ {X} $ of $ \xi $ to $ X $ is stably non-trivial (i.e., $ X $ is the support of $ \xi $). Then there always exists a globally-minimal surface $ X _ {0} \in X( \xi ) $ having least volume in the class $ X( \xi ) $. The general existence theorem can be formulated and proved also in the language of integral currents, for which one introduces filtered currents consisting of currents with various dimensions. In this way a solution to the multi-dimensional Plateau problem was obtained in homotopy classes of multi-varifolds [14].
In the circle of problems related to the multi-dimensional Plateau problem one may distinguish research on particular analytic and topological features of globally-minimal surfaces. For example, there is the current problem of representing particular surfaces in Riemannian spaces. For example, it is known [3] that complex-algebraic subvarieties in $ \mathbf C ^ {n} $ and $ \mathbf C P ^ {n} $ are globally-minimal surfaces. One of the results has an explicit complex character. In the case of real subvarieties, for a long time there were no methods for detecting particular globally-minimal surfaces. The first result in this field [6], which incorporated the topology, was a method that enabled one to show that each compact Riemannian space $ M ^ {n} $ can be put into correspondence with a universal function $ \Omega _ {x} ( k) $, where $ x \in M ^ {n} $ and $ k $ is an integer, $ 1 \leq k \leq n $. If $ X _ {0} $ is a globally-minimal surface that realizes a non-trivial (co)cycle in $ H _ {k} ( M ^ {n} ) $, then $ \mathop{\rm vol} _ {k} X _ {0} \geq \Omega _ {x} ( k) $ for any point $ x \in X _ {0} $. If $ M = G/H $ is a homogeneous space, then $ \Omega _ {x} ( k) \equiv \Omega ( k) $ is independent of the point $ x $. The function $ \Omega _ {x} ( k) $ is calculated in explicit form and gives a general lower bound to the volumes of all $ k $-dimensional (co)cycles in $ M ^ {n} $. This bound cannot be improved in the general case, i.e. there exist infinite series of globally-minimal films $ X _ {0} $ for which $ \mathop{\rm vol} _ {k} X _ {0} = \Omega ( k) $. A result for symmetric spaces ([6], , [15]) is a complete description of all surfaces for which $ \mathop{\rm vol} _ {k} X _ {0} = \Omega ( k) $. Further methods have been devised [11], [12], [14], [15] for obtaining particular globally-minimal surfaces.
There are various problems in variational calculus, topology, algebraic geometry, and complex analysis that give rise to the following situation: One is given a manifold $ M ^ {n} $ and an exhaustion of it by $ n $-dimensional regions $ D _ {r} $ that expand as the parameter $ r $ increases; in $ M ^ {n} $, there is a definite globally-minimal surface $ X ^ {k} $; the question is raised of the rate at which $ \mathop{\rm vol} _ {k} ( X ^ {k} \cap D _ {r} ) $ increases, considered as a function of $ r $. This question arises for example in the calculation of $ \Omega _ {x} ( k) $, in the problem of the structure of bases in spaces of entire functions, in theorems of Stoll type [11], etc. It has been found [6], [15] that there exists a universal exact effectively-computable lower bound to the rate of increase of $ \mathop{\rm vol} _ {k} ( X ^ {k} \cap D _ {r} ) $, which implies as particular cases explicit formulas for $ \mathop{\rm vol} _ {k} X ^ {k} $, where $ X ^ {k} $ is a globally-minimal surface. For example, the volume of such a surface enclosed in a sphere $ B ^ {n} \subset \mathbf R ^ {n} $ and passing through the centre of the sphere (and having its boundary at the boundary of the sphere) is always at least that of a standard $ k $- dimensional sphere $ B ^ {k} $ (a planar section) passing through the centre of $ B ^ {n} $, [15].
A particular line of research is represented by the multi-dimensional Plateau problem of codimension one: One considers globally-minimal surfaces of codimension 1 in $ \mathbf R ^ {n} $. For example, Bernstein's problem (S.N. Bernshtein) has been solved [7]: Let $ V ^ {n-1} $ be a smooth complete locally-minimal submanifold in $ \mathbf R ^ {n} $ allowing of one-to-one projection onto a certain hyperplane, i.e. $ V ^ {n-1} $ is given by the graph of a function $ f $ defined in $ \mathbf R ^ {n-1} $; is it true that $ f $ is a linear function? The answer is positive for $ 3\leq n\leq 8 $[8]. The minimality of such hypersurfaces is closely related to the minimality of cones in $ \mathbf R ^ {n} $: The existence of a locally-minimal surface implies the existence of a minimal cone $ CM ^ {n-2} $, i.e. of a surface composed of points on radii running from a point $ O \in \mathbf R ^ {n} $ to points $ x \in M ^ {n-2} $, where $ M ^ {n-2} $ is a locally-minimal surface in the sphere $ S ^ {n-1} $. It has been established [8] that if $ M ^ {n-2} $ is a closed locally-minimal submanifold (i.e. one that annihilates the Euler operator) in $ S ^ {n-1} $ that is not the equator $ S ^ {n-2} \subset S ^ {n-1} $, then for $ n \leq 7 $ the cone $ CM ^ {n-2} $ with base $ M ^ {n-2} $ and vertex at the centre of the sphere does not minimize the $ ( n- 1) $-dimensional volume $ \mathop{\rm vol} _ {n-1} $ (for a fixed boundary in $ M ^ {n-2} $), i.e. there exists a variation (with support localized around the centre of the sphere) that reduces the volume of the cone. This implies that $ f $ is a linear function for $ n < 9 $. For $ n= 9 $ the answer is negative: There exist [7] locally- and even globally-minimal surfaces $ V ^ {n-1} \subset \mathbf R ^ {n} $ defined as graphs of non-linear functions. The construction can be performed explicitly; it is then found that cones specified in $ \mathbf R ^ {2m} $ by the equation
$$ \tag{* } x _ {1} ^ {2} + \dots + x _ {m} ^ {2} = x _ {m+1} ^ {2} + \dots + x _ {2m} ^ {2} $$
are globally-minimal surfaces with a fixed boundary $ V = S ^ {m-1} \times S ^ {m-1} $, $ m \geq 4 $. These cones represent a particular case of cones of more general form that are globally-minimal surfaces [10].
There is a new line of research on the multi-dimensional Plateau problem, namely that of equivariant multi-dimensional Plateau problems. Among the globally-minimal surfaces, one naturally distinguishes the class of films that are transformed into themselves under the action of a certain symmetry group [9], [10]. Let $ G $ be a compact connected Lie group acting smoothly on $ M ^ {n} $ by isometries and stratifying it into orbits $ G( x) $, $ x \in M ^ {n} $. Then to find the globally-minimal surfaces $ X ^ {k} $ in $ M ^ {n} $ that are invariant with respect to $ G $ it is sufficient to transfer to the quotient space $ P = M ^ {n} /G $ and endow $ P $ with a Riemannian metric of the form
$$ dl _ {p} = v ^ {1/p} d \widetilde{s} , $$
where $ v = \mathop{\rm vol} G( x) $ and
$$ p = \mathop{\rm dim} X ^ {k} - \mathop{\rm dim} G( x) = k - \mathop{\rm dim} G( x), $$
where $ \mathop{\rm dim} G( x) $ denotes the dimension of an orbit in general position in $ M ^ {n} $ and $ d \widetilde{s} $ is the natural projection metric arising in $ P $ under the isometric action of $ G $. To find globally-minimal surfaces in $ M ^ {n} $ invariant with respect to $ G $ it is sufficient to describe such surfaces in $ M ^ {n} /G $ endowed with the metric $ dl _ {p} $[9], so one gets a reduction of the multi-dimensional Plateau problem in $ M ^ {n} $ to the same problem in $ M ^ {n} /G $ in fewer dimensions. This method has provided a number of particular globally-minimal surfaces having large symmetry groups .
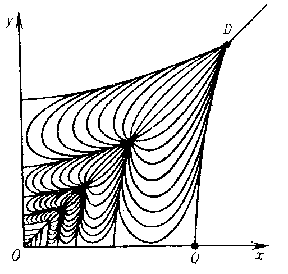
Figure: p072850b
In particular, "Simons cones" , defined by (*), are represented by the line $ OD $ (Fig. b) on the two-dimensional quotient space
$$ {\mathbf R ^ {2m} } / { \mathop{\rm SO} _ {m} } \times \mathop{\rm SO} _ {m} = \{ x \geq 0, y\geq 0 \} , $$
endowed with the metric
$$ ( xy) ^ {2(2m- 2)} ( dx ^ {2} + dy ^ {2} ) $$
and representing the first quadrant $ K $ in the plane $ \mathbf R ^ {2} $[10]. To find a globally-minimal surface with boundary
$$ S ^ {m-1} \times S ^ {m-1} = G( D),\ \ G = \mathop{\rm SO} _ {m} \times \mathop{\rm SO} _ {m} , $$
it is sufficient to find geodesics running from $ D $ to the boundary of $ K $ and having minimum length. Fig. bshows a pencil of geodesics running from $ D $; this pencil can be understood as a pencil of light rays propagating from a source $ D $ in a transparent medium filling $ K $ with refraction index $ ( xy) ^ {2m-2} $. For $ m< 5/2+ \sqrt 2 $, in addition to the surface $ OD $ there exists a further minimal solution of smaller length, which is represented by the geodesic $ OQ $; this means that this Simons cone is not a globally-minimal surface. As $ m $ increases, the point $ Q $ tends to $ O $, and for $ m> 5/2+ \sqrt 2 $ there exists a unique geodesic joining $ D $ to the boundary of the quadrant, i.e. this Simons cone is a globally-minimal surface [10].
References
| [1] | C. Morrey, "Multiple integrals in the calculus of variations" , Springer (1966) MR0202511 Zbl 0142.38701 |
| [2] | E. Reifenberg, "Solution of Plateau's problem for 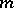 -dimensional surfaces of varying topological type" Acta Math. , 104 : 1/2 (1960) pp. 1–92 -dimensional surfaces of varying topological type" Acta Math. , 104 : 1/2 (1960) pp. 1–92 |
| [3] | H. Federer, "Geometric measure theory" , Springer (1969) MR0257325 Zbl 0176.00801 |
| [4] | F.J. Almgren, "Existence and regularity almost everywhere of solutions to elliptic variational problems among surfaces of varying topological type and singularity structure" Ann. of Math. (2) , 87 : 2 (1968) pp. 321–391 MR0225243 Zbl 0162.24703 |
| [5] | A.T. Fomenko, "The multidimensional Plateau problem in Riemannian manifolds" Math. USSR Sb. , 18 : 3 (1972) pp. 487–527 Mat. Sb. , 89 : 3 (1972) pp. 475–519 MR0348599 Zbl 0276.49032 |
| [6] | A.T. Fomenko, "Minimal compacta in Riemannian manifolds and Reifenberg's conjecture" Math. USSR Izv. , 6 : 5 (1972) pp. 1037–1066 Izv. Akad. Nauk SSSR Ser. Mat. , 36 : 5 (1972) pp. 1049–1079 |
| [7] | E. Bombieri, E. de Giorgi, E. Giusti, "Minimal cones and the Bernstein problem" Invent. Math. , 7 : 3 (1969) pp. 243–268 MR0250205 Zbl 0183.25901 |
| [8] | J. Simons, "Minimal varieties in Riemannian manifolds" Ann. of Math. , 88 : 1 (1968) pp. 62–105 MR0233295 Zbl 0181.49702 |
| [9] | H. Lawson, "The equivalent Plateau problem and interior regularity" Trans. Amer. Math. Soc. , 173 : 446 (1972) pp. 231–249 |
| [10] | H. Lawson, J. Simons, "On stable currents and their application to global problems in real and complex geometry" Ann. of Math. , 98 : 3 (1973) pp. 427–450 MR0324529 Zbl 0283.53049 Zbl 0594.53037 |
| [11] | A.T. Fomenko, "Bott periodicity from the point of view of an  -dimensional Dirichlet functional" Math. USSR Izv. , 5 : 3 (1971) pp. 681–695 Izv. Akad. Nauk SSSR Ser. Mat. , 35 : 3 (1971) pp. 667–681 -dimensional Dirichlet functional" Math. USSR Izv. , 5 : 3 (1971) pp. 681–695 Izv. Akad. Nauk SSSR Ser. Mat. , 35 : 3 (1971) pp. 667–681 |
| [12] | Dao Chong Tkhi, "Multivarifolds and classical multidimensional Plateau problems" Math. USSR Izv. , 17 (1981) pp. 271–298 Izv. Akad. Nauk SSSR Ser. Mat. , 44 : 5 (1980) pp. 1031–1065 Zbl 0504.58015 |
| [13a] | A.T. Fomenko, "Multidimensional Plateau problem in Riemannian manifolds and extraordinary homology and cohomology theories I" , Proc. Sem. Vektor. Tenzor. Anal. , 17 (1974) pp. 3–176 (In Russian) MR433501 |
| [13b] | A.T. Fomenko, "Multidimensional Plateau problem in Riemannian manifolds and extraordinary homology and cohomology theories II" , Proc. Sem. Vektor. Tenzor. Anal. , 18 (1978) pp. 4–93 (In Russian) MR504523 |
| [14] | Dao Chong Tkhi, "On the stability of the homology of compact Riemannian manifolds" Math. USSR Izv. , 12 (1978) pp. 463–468 Izv. Akad. Nauk SSSR Ser. Mat. , 42 : 3 (1978) pp. 500–505 Zbl 0416.58003 |
| [15] | A.T. Fomenko, "Multi-dimensional variational methods in the topology of extremals" Russian Math. Surveys , 36 : 6 (1981) pp. 127–165 Uspekhi Mat. Nauk , 36 : 6 (1981) pp. 125–169 MR643070 |
| [16] | W.Y. Hsiang, H.B. Lawson, "Minimal submanifolds of low cohomogenety" J. Diff. Geom. , 5 : 1 (1971) pp. 1–38 |
| [17] | J.E. Brothers, "Invariance of solutions to invariant parametric variational problems" Trans. Amer. Math. Soc. , 262 : 1 (1980) pp. 159–180 MR0583850 Zbl 0471.49038 |
| [18a] | R. Harvey, H.B. Lawson, "On boundaries of complex analytic varieties I" Ann. of Math. , 102 (1975) pp. 233–290 MR0425173 Zbl 0317.32017 |
| [18b] | R. Harvey, H.B. Lawson, "On boundaries of complex analytic varieties II" Ann. of Math. , 106 (1977) pp. 213–238 MR0499285 Zbl 0361.32010 |
| [19] | R. Harvey, H.B. Lawson, "Calibrated geometries" Acta Math. , 148 (1982) pp. 47–157 MR0666108 Zbl 0584.53021 |
| [20] | S.S.-T. Yau, "Kohn–Rossi cohomology and its application to the complex Plateau problem" Ann. of Math. , 113 : 1 (1981) pp. 67–110 MR0604043 Zbl 0464.32012 |
| [21] | W.H. Meeks, S.S.-T. Yau, "The classical Plateau problem and the topology of three-dimensional manifolds. The embedding of the solution given by Dehn's lemma" Topology , 21 : 4 (1982) pp. 409–442 MR0670745 |
| [22] | A.T. Fomenko, "Plateau problem" , 1–2 , Gordon & Breach (1990) (Translated from Russian) MR1055827 MR1055826 Zbl 0729.53001 |
Comments
For minimal surfaces in $ \mathbf C ^ {n} $ see also [a4], [a5].
References
| [a1] | A.T. Fomenko, "Variational principles in topology - Multidimensional minimal surface theory" , Kluwer (1990) (Translated from Russian) Zbl 0697.49044 |
| [a2] | E. Giusti, "Minimal surfaces and functions of bounded variation" , Birkhäuser (1984) MR0775682 Zbl 0545.49018 |
| [a3] | A.T. Fomenko, Dao Chong Tkhi, "Minimal surfaces and Plateau's problem" , Amer. Math. Soc. (Forthcoming) (Translated from Russian) |
| [a4] | G. Stolzenberg, "Volumes, limits, and extensions of analytic varieties" , Springer (1966) MR0206337 Zbl 0142.33801 |
| [a5] | E.M. Chirka, "Complex analytic sets" , Kluwer (1989) pp. §19 (Translated from Russian) MR1111477 Zbl 0683.32002 |
Plateau problem, multi-dimensional. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plateau_problem,_multi-dimensional&oldid=52157