Osculating plane

at a point $M$ of a curve $l$

The plane having contact of order $n\geq2$ with $l$ at $M$ (see Osculation). The osculating plane can also be defined as the limit of a variable plane passing through three points of $l$ as these points approach $M$. Usually, a curve intersects the osculating plane at the point of contact (see Fig.).

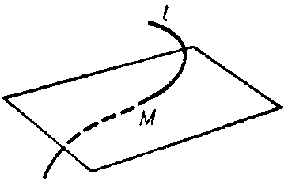
Figure: o070560a

If $l$ is given by equations

$$x=x(u),\quad y=y(u),\quad z=z(u),$$

then the equation of the osculating plane has the form

$$\begin{vmatrix}X-x&Y-y&Z-z\\x'&y'&z'\\x''&y''&z''\end{vmatrix}=0,$$

where $X,Y,Z$ are moving coordinates and $x,y,z$, $x',y',z'$, $x'',y'',z''$ are calculated at the point of contact. If all three coefficients of $X,Y,Z$ in the equation of the osculating plane vanish, then the osculating plane becomes indefinite (and can coincide with any plane through the tangent line).

References

[a1]	R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 31–35
[a2]	D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 10ff

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️