Osculating circle
at a given point $M$ of a curve $l$
The circle that has contact of order $n\geq2$ with $l$ at $M$ (see Osculation). If the curvature of $l$ at $M$ is zero, then the osculating circle degenerates into a straight line. The radius of the osculating circle is called the radius of curvature of $l$ at $M$, and its centre the centre of curvature (see Fig.). If $l$ is the plane curve given by an equation $y=f(x)$, then the radius of the osculating circle is given by
$$\rho=\left|\frac{(1+y'^2)^{3/2}}{y''}\right|.$$
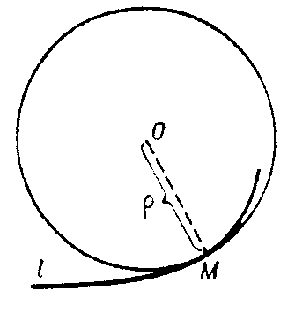
Figure: o070540a
If $l$ is the spatial curve given by equations
$$x=x(u),\quad y=y(u),\quad z=z(u),$$
then the radius of the osculating circle is given by
$$\rho=\frac{(x'^2+y'^2+z'^2)^{3/2}}{\sqrt{(y'z''-z'y'')^2+(z'x''-x'z'')^2+(x'y''-y'z'')^2}}$$
(where the primes denote differentiation with respect to $u$).
References
| [a1] | R.S. Millman, G.D. Parker, "Elements of differential geometry" , Prentice-Hall (1977) pp. 39 |
| [a2] | D.J. Struik, "Lectures on classical differential geometry" , Dover, reprint (1988) pp. 14 |
Osculating circle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Osculating_circle&oldid=54036