Rigidity

This page is deficient and requires revision. Please see Talk:Rigidity for further comments.

The property of an immersed submanifold $ M $ of a Riemannian space $ V $ defined by the fact that each of its isometric deformations (cf. Infinitesimal deformation) is trivial, that is, the corresponding velocity field $ z $ on $ M $ is induced by a Killing vector field $ \zeta $ on $ M $: $ z = \zeta \circ i $, where $ i : M \rightarrow V $ is the isometric immersion of $ M $ into $ V $. The question of the rigidity of a submanifold — essentially that of the uniqueness of the solution of the system of differential equations that are the linearizations of the fundamental system of equations in the theory of surfaces — has practically never been considered in the case where $ \mathop{\rm dim} M > 2 $ and $ \mathop{\rm dim} V > 3 $; however, in the simplest situation $ ( \mathop{\rm dim} M = \mathop{\rm dim} V - 1 = 2 ) $, it has been possible to construct a more-or-less complete theory for surfaces of positive curvature contained in spaces of constant curvature (see Vekua method). Only isolated results are known about the rigidity of surfaces of non-positive or mixed curvature; it turns out that the degree of regularity of the deformations under discussion has influence on the rigidity of a surface, apart from its shape in space.

As a rule, a non-closed surface is non-rigid, but: a) examples have been made of surfaces with a flat point $ m $ every neighbourhood of which is rigid or allows an infinitesimal deformation of bounded regularity; and b) there exist rigid non-closed convex surfaces of total curvature $ 4 \pi $, bordered by plane parabolic curves (parts of surfaces of type $ T $).

The extent of the restriction of the mobility of the boundary of the surfaces or of curves inside it influences the rigidity of a surface; for example: 1) spherical segments $ S $ sliding along a plane will be rigid or not according to as a hemisphere is smaller or larger than $ S $; 2) a piece of a hyperbolic paraboloid with two intersecting fixed generators is rigid; and 3) a piece of the plane with a fixed boundary is not rigid.

Closed surfaces have been studied in more detail from the point of view of their rigidity; for example, $ \alpha $) a closed convex surface is rigid (see the Blaschke–Weyl formula, and also [2]); $ \beta $) at the same time, there are non-rigid closed surfaces of revolution of mixed curvature; $ \gamma $) a torus is rigid; $ \delta $) a closed cylindroid is rigid if and only if the area of the mean section satisfies the equation

$$ S _ {\textrm{ me } } = \frac{1}{4} ( S _ {1} + S _ {2} ) , $$

where $ S _ {1} $ and $ S _ {2} $ are the areas of the upper and lower bases; and $ \epsilon $) the metric product of $ k $ two-dimensional spheres is rigid in the Euclidean space $ E ^ {3k} $ and not rigid in $ E ^ {3k+} l $ for $ l > 0 $.

The concept of rigidity here defined is sometimes called first-order rigidity. Rigidities of second and higher orders have also been introduced. The concept of rigidity carries over to non-regular surfaces, for example, to polyhedra; however, the main results there relate to convex polyhedra (see Cauchy theorem on polyhedra), and to surfaces in Riemannian spaces, for example, closed surfaces of arbitrary genus and of positive extremal curvature are rigid.

References

[1]	N.V. Efimov, "Qualitative problems of the theory of deformation of surfaces" Uspekhi Mat. Nauk , 3 : 2 (1948) pp. 47–158 (In Russian)
[2]	A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1973) (Translated from Russian)
[3]	S.E. Cohn-Vossen, "Some problems of differential geometry in the large" , Moscow (1959) (In Russian)
[4]	I.N. Vekua, "Generalized analytic functions" , Pergamon (1962) (Translated from Russian)
[5]	A.D. Aleksandrov, "Konvexe Polyeder" , Akademie Verlag (1958) (Translated from Russian)
[6]	V.T. Fomenko, "Single-valued determination of closed surfaces of genus 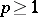in a space of constant curvature" Math. Notes , 16 : 3 (1974) pp. 852 Mat. Zametki , 16 : 3 (1974) pp. 441–445

References

[a1]	H. Huck, R. Roitzsch, U. Simon, W. Vortisch, R. Walden, B. Wegner, W. Wendland, "Beweismethoden der Differentialgeometrie im Grossen" , Lect. notes in math. , 335 , Springer (1973)