Isometric immersion

An immersion (cf. Immersion of a manifold) of a $ k $- dimensional metric manifold $ M ^ {k} $ into an $ n $- dimensional Riemannian space $ V ^ {n} $, $ n \geq k $, as a $ k $- dimensional surface $ \Phi $, such that the distance between any two points in $ M ^ {k} $ is the same as the distance between their images measured along the surface $ \Phi $ in $ V ^ {n} $. This definition can be generalized if the Riemannian space is replaced by a more general metric space. A special case of an isometric immersion is an isometric imbedding — a one-to-one immersion.

The main problems in the theory of isometric immersions are: 1) the possibility of an isometric immersion of a given manifold into a given space; and 2) the problem of uniqueness, if an isometric immersion exists. These problems are considered under various conditions on the manifold and its isometric image — smoothness, regularity, analyticity, convexity, etc. Under each of these conditions the main problems in the theory of isometric immersions take the following form: a) the question of global isometric immersion of $ M ^ {k} $ into $ V ^ {n} $; b) the question of local isometric immersion of $ M ^ {k} $ into $ V ^ {n} $( i.e. the isometric immersion of a sufficiently small neighbourhood of a distinguished point $ v \in M ^ {k} $ into $ V ^ {n} $); c) in the local and the global cases, the determination of the smallest $ p $ such that $ M ^ {k} $ can be immersed (imbedded) into the Euclidean space $ E ^ {k + p } $ of dimension $ k + p $( the number $ p $ is called the immersion class, respectively imbedding class, of $ M ^ {k} $); and d) the problem of the isometric deformation of a given immersion.

From the analytic point of view, the question of the existence of an isometric immersion of $ M ^ {k} $ into $ V ^ {n} $ is equivalent to the solution of a system of non-linear partial differential equations. For an isometric immersion into $ E ^ {n} $, this system has the form

$$ \sum _ {\alpha = 1 } ^ { n } \frac{\partial x ^ \alpha }{\partial u ^ {i} } \frac{\partial x ^ \alpha }{\partial u ^ {j} } = \ g _ {ij} , $$

where $ x = \{ x ^ \alpha ( u ^ {s} ) \} $ is the desired isometric immersion and $ g _ {ij} $ is the metric tensor of $ M ^ {k} $ in the local coordinates $ u ^ {1} \dots u ^ {k} $. For the solution of this system in the global case, use is made of the so-called free mapping $ x $ into $ E ^ {n} $( see Nash theorems (in differential geometry)). For the local analytic case, the Cauchy–Kovalevskaya theorem is used instead of an implicit-function theorem. The role of the free mapping and the implicit-function theorem remains the same in the general case for immersions of class $ C ^ {r} $, $ 2 \leq r \leq \infty $ or $ r = \omega $, into Riemannian and pseudo-Riemannian spaces. Different methods are used for isometric immersions of class $ C ^ {1} $. These are based on deformations of the immersion, enabling one to change the immersion while keeping track of the variation in the metric. In investigating isometric immersions into $ E ^ {n} $, the Gauss–Meinardi–Codazzi equations are also used (cf. Peterson–Codazzi equations).

Global isometric immersion.

Every compact Riemannian manifold $ M ^ {k} $ of class $ C ^ {r} $( $ 3 \leq r \leq \infty $) has an isometric imbedding of class $ C ^ {r} $ into every ball in $ E ^ {n} $, for some $ n \leq ( 3k ^ {2} + 11k)/2 $; if $ M ^ {k} $ is not compact, then it has an imbedding of class $ C ^ {r} $ into any part of $ E ^ {n} $, where $ 3 \leq r \leq \infty $, for some $ n \leq ( 3k ^ {2} + 11k) ( k + 1)/2 $( see [6]). The dimension of the space $ E ^ {n} $ can be reduced in the cases $ r = \infty $ and $ r = \omega $: Every Riemannian manifold $ M ^ {k} $( compact or not, with or without boundary) of class $ C ^ \infty $( $ C ^ \omega $) has an isometric imbedding of class $ C ^ \infty $( $ C ^ \omega $) into $ E ^ {n} $, for some $ n \leq 3k + 5 + k ( k + 1)/2 $.

For a $ k $- dimensional hyperbolic space $ ( k > 2) $ an isometric imbedding of class $ C ^ \omega $ into $ E ^ {6k - 5 } $ has been obtained in explicit form, and an isometric imbedding of class $ C ^ \omega $ into $ E ^ {n} $, $ n = k ( k + 3)/2 $, for a $ k $- dimensional elliptic space has also been obtained.

In the results here listed, the smoothness of the surface $ \Phi $ is not greater than that of the immersed metric. This fact is not accidental; indeed, every $ k $- dimensional surface $ \Phi $( $ 1 \leq k \leq n - 1 $) of class $ C ^ {r, \alpha } $, $ r \geq 2 $, $ 0 \leq \alpha < 1 $, into $ E ^ {n} $ is an isometric immersion of class $ C ^ {r, \alpha } $ of some Riemannian manifold $ M ^ {k} $ of class $ C ^ {r, \alpha } $( see [8]).

A lower bound for the dimension of the spaces $ E ^ {n} $ into which an isometric immersion of a Riemannian manifold can be realized is given by the following theorem: Suppose that a compact Riemannian manifold $ M ^ {k} $ of class $ C ^ {4} $ has the following property: At each point of $ M ^ {k} $ there exists a $ q $- plane such that all curvatures in all two-dimensional directions in it are non-positive; then $ M ^ {k} $ does not have an isometric immersion of class $ C ^ {4} $ into any $ E ^ {n} $ with $ n \leq k + q - 1 $; if the condition imposed on the curvature of $ M ^ {k} $ is restricted to a single point and $ q = n $, then there exists an isometric immersion of class $ C ^ {4} $ into $ E ^ {2k - 2 } $. For example, a flat $ k $- dimensional torus does not have an isometric immersion of class $ C ^ {4} $ into $ E ^ {2k - 1 } $; if $ k $ is a power of 2, then the real projective space $ \mathbf R P ^ {k} $ endowed with a metric with everywhere-positive scalar curvature, in particular, a $ k $- dimensional elliptic space, does not have an isometric immersion of class $ C ^ {2} $ into $ E ^ {2k} $.

Results concerning the isometric immersions of class $ C ^ {1} $ are sharply different from the preceding ones. They can be stated as follows: If a compact Riemannian manifold $ M ^ {k} $ of class $ C ^ {0} $( with or without boundary) has an immersion of class $ C ^ {1} $ into $ E ^ {n} $ with $ n \geq k + 1 $, then it also has an isometric immersion of class $ C ^ {1} $ into $ E ^ {n} $; if a non-compact Riemannian manifold $ M ^ {k} $ of class $ C ^ {0} $ has a short immersion (that is, one not extending the line element at each point) of class $ C ^ {1} $ into $ E ^ {n} $, $ n \geq k + 1 $, not intersecting its limit set, then it has an isometric immersion of class $ C ^ {1} $ into $ E ^ {n} $( see [7]) (here the limit set of an immersion of a manifold $ M ^ {k} $ into $ E ^ {n} $ is the set of points $ x $ of $ E ^ {n} $ such that there is a divergent sequence of points of $ M ^ {k} $ the image of which in $ E ^ {n} $ converges to $ x $). In particular, every compact Riemannian manifold $ M ^ {k} $ of class $ C ^ {0} $( with or without boundary) has an isometric immersion of class $ C ^ {1} $ into $ E ^ {2k} $; every non-compact Riemannian manifold of class $ C ^ {0} $ has an isometric immersion of class $ C ^ {1} $ into $ E ^ {2k + 1 } $.

If isometric immersions (isometric imbeddings) of class $ C ^ {1} $ of a Riemannian manifold $ M ^ {k} $ into $ E ^ {n} $ with $ n > k $ can be joined by a short regular homotopy (a short diffeotopy), then they can be joined by a deformation consisting of isometric immersions (isometric imbeddings) of class $ C ^ {1} $. In particular, in the compact case isometric immersions (isometric imbeddings) of class $ C ^ {1} $ can be joined by a deformation consisting of isometric immersions (isometric imbeddings) of class $ C ^ {1} $ if and only if they are regularly homotopic (regularly diffeotopic).

Local isometric immersions.

In 1873, L. Schläfli conjectured that every Riemannian manifold of dimension $ k $ has a local isometric immersion into the Euclidean space $ E ^ {n} $, $ n = k ( k + 1)/2 $. This conjecture has been established only for analytic manifolds (see Janet theorem); i.e., in every Riemannian manifold $ M ^ {k} $ of class $ C ^ \omega $ there exists a neighbourhood of an arbitrary point having an isometric imbedding of class $ C ^ \omega $ into $ E ^ {n} $, where $ n = k ( k + 1)/2 $. In a Riemannian space $ M ^ {k} $ of class $ C ^ \infty $ there exists a neighbourhood of an arbitrary point having an isometric imbedding of class $ C ^ \infty $ into $ E ^ {n} $ where $ n = k + k ( k + 1)/2 $( see [7]). On the other hand, for every Riemannian manifold of class $ C ^ {0} $ there is a neighbourhood of an arbitrary point having an isometric imbedding of class $ C ^ {1} $ into $ E ^ {k + 1 } $.

The discovery of conditions under which a given manifold $ M ^ {k} $ has an isometric immersion into $ E ^ {n} $, $ n < k ( k + 1)/2 $, goes in quite different directions. This is connected with the fact that not every Riemannian manifold $ M ^ {k} $ has an isometric immersion into $ E ^ {n} $: For $ r \geq k ^ {2} ( k + 1)/2 - k $, $ r - 1 \leq l \leq \infty $, the set of Riemannian metrics that are locally induced on a smooth manifold $ M ^ {k} $ by the local imbeddings of class $ C ^ {r} $ into $ E ^ {n} $, $ n < k ( k + 1)/2 $, is nowhere dense in the set of all Riemannian metrics of class $ C ^ {l} $ on $ M ^ {k} $, endowed with the usual $ C ^ {l} $- topology; for $ r = 2 $ and $ 2 \leq l \leq \infty $, this assertion remains true if $ n $ and $ k $ are related by the inequality $ n < ( k + 1 + k ( k + 1)/2)/3 $.

In the solution of the problem of determining the isometric immersion class (see above) of a manifold, the minimum $ p $ found in the local formulation also bounds from below the value of $ p $ for a global isometric immersion. However, the exact value of the smallest $ p $ such that every manifold $ M ^ {k} $, $ k > 2 $, of class $ C ^ {r} $, $ 2 \leq r \leq \infty $, has an isometric immersion of class $ C ^ {r} $ into $ E ^ {k + p } $ is unknown. There are some special devices for calculating the isometric immersion class of a given Riemannian manifold $ M ^ {k} $ into $ E ^ {n} $. Thus, $ p = 0 $ if and only if the curvature tensor of $ M ^ {k} $ is identically zero. There exists an algebraic criterion for determining whether the isometric immersion class is 1, based on the fact that under certain additional assumptions, the Peterson–Codazzi equations are a consequence of the Gauss equation for metrics of class 1 [11]. In particular, the metrics of constant positive curvature have class 1 and, for $ k > 3 $, are realized in the form of hyperspheres in a Euclidean space. But if the Ricci curvature of $ M ^ {k} $ is zero, then $ p \neq 1 $.

Almost all results discussed here can be generalized to isometric immersions from one Riemannian space into another. This is the case, for example, for immersions of class $ C ^ {1} $, for local isometric immersions, for sufficiently-smooth isometric immersions of $ k $- dimensional manifolds into a $ V ^ {n} $ of sufficiently-large dimension, for the connections between the orders of smoothness of surfaces and their metrics, etc.

Questions of isometric immersibility carry over to pseudo-Riemannian manifolds. In this case, in addition to the dimensions $ k $ and $ n $, use is made of the dimensions $ k _ {+} $ and $ k _ {-} = k - k _ {+} $ of the positive and negative parts of the metric tensor on the immersed manifold $ M ^ {k} $ and the analogous dimensions $ n _ {+} $ and $ n _ {-} = n - n _ {+} $ of the ambient space $ V ^ {n} $. E.g., Janet's theorem holds in the pseudo-Riemannian case with $ n \geq k ( k + 1)/2 $, $ n _ {+} \geq k _ {+} $, $ n _ {-} \geq k _ {-} $.

Isometric immersions of two-dimensional manifolds.

Many problems of this type have been solved completely in the sense that the space into which the immersion is to be constructed has minimal dimension. Here, special methods of solution have been developed, based on the general theory of non-linear partial differential equations and topological-geometric considerations.

The Weyl problem, posed in 1916, states: Does a two-dimensional Riemannian manifold $ M ^ {2} $ have an isometric immersion into $ E ^ {3} $ if it is homeomorphic to a sphere and has positive Gaussian curvature? A complete solution of the Weyl problem, generalized to the case concerning isometric immersibility of an $ M ^ {2} $ into a three-dimensional Riemannian space $ V ^ {3} $, was given by A.V. Pogorelov [3]: Let $ V ^ {3} $ be a complete three-dimensional Riemannian space, and let $ M _ {+} ^ {2} $ be a closed topological sphere equipped with a Riemannian structure having Gaussian curvature everywhere greater than some constant $ k _ {0} $( greater than, equal to, or less than zero). If the curvature of the ambient space is everywhere less than $ k _ {0} $, then $ M _ {+} ^ {2} $ has an isometric immersion into $ V ^ {3} $ as a regular surface $ \Phi $. This immersion can be brought in such a position that a given two-dimensional element $ \alpha $ of $ M _ {+} ^ {2} $( a point and a pencil of directions at it) coincides with a given two-dimensional element $ \alpha ^ \prime $ in $ V ^ {3} $ isometric with $ \alpha $, and the surface is located in the direction given by $ \alpha ^ \prime $. If the metrics of $ V ^ {3} $ and $ M _ {+} ^ {2} $ belong to $ C ^ {r} $, $ r \geq 3 $, then $ \Phi $ belongs at least to $ C ^ {r - 1, \nu } $, $ 0 < \nu < 1 $. The surface is determined uniquely by the two-dimensional element. Every two isometric immersions of class $ C ^ {r} $, $ r \geq 3 $, $ r = \omega $, into $ V ^ {3} $ can be joined by a deformation consisting of isometric immersions in the same class.

The Weyl problem has been investigated from a completely different point of view by A.D. Aleksandrov, who has constructed a theory of (non-regular) two-dimensional manifolds with a convex metric [4] (such manifolds can be defined as limits of regular manifolds with positive Gaussian curvature) and suggested the following plan for the solution of the Weyl problem: 1) generalize the statement of the problem by taking for $ M ^ {2} $ a manifold with an arbitrary, in general non-regular, metric; 2) then establish regularity of an isometric immersion in accordance with that of the metric in $ M ^ {2} $. The accomplishment (by him) of the first part of this plan leads to an exhaustive result: Every manifold that is homeomorphic to a sphere, and with a convex metric, has an isometric immersion into $ E ^ {3} $ in the form of a closed convex surface. The realization of the second part of the plan was achieved by Pogorelov [3], where the problem of the regularity of a convex surface with a regular metric was solved completely: If a convex surface $ \Phi \subset E ^ {3} $ has a metric of class $ C ^ {k, \alpha } $, $ k \geq 2 $, $ 0 < \alpha < 1 $, and has positive Gaussian curvature, then $ \Phi $ belongs to $ C ^ {k, \alpha } $. If the metric of $ \Phi $ is analytic, then $ \Phi $ is itself analytic. Similar theorems hold for convex surfaces in a space of constant curvature. Under certain conditions there exist isometric immersions of two-dimensional Riemannian manifolds of positive Gaussian curvature that are homeomorphic to the plane or the disc. In addition to this, examples have been constructed of analytic metrics of positive curvature defined on the disc and not having isometric immersions of class $ C ^ {2} $ into $ E ^ {3} $.

Hilbert's theorem stating that the Lobachevskii plane has no isometric immersion of class $ C ^ {2} $ into $ E ^ {3} $ naturally led to the problem: Do some complete two-dimensional metrics with curvature bounded from above by a negative constant (the so-called metrics of type $ \Lambda $) have immersions into $ E ^ {3} $? The solution of this problem was given by N.V. Efimov [14]: If $ \Phi $ is a complete surface of class $ C ^ {2} $ in $ E ^ {3} $ with Gaussian curvature $ K ( x) $, then $ \sup _ {x \in \Phi } K ( x) \geq 0 $, so that, in particular, metrics of type $ \Lambda $ do not have immersions into $ E ^ {3} $. In this connection, the question as to which parts of metrics of type $ \Lambda $( that is, domains in two-dimensional manifolds on which these metrics are given) can be immersed in $ E ^ {3} $ is of interest. A specific answer to this question was obtained in [15]. Suppose that the line element $ ds ^ {2} = dx ^ {2} + B ^ {2} ( x, y) dy ^ {2} $ is given on the infinite strip

$$ \Pi _ {a} = \{ 0 \leq x \leq a , - \infty < y < + \infty \} $$

in $ E ^ {2} $ with Cartesian coordinates $ x $, $ y $, where $ B \in C ^ {r, 1 } $, $ r \geq 3 $, has the following properties: a) itself, all its $ r $- th derivatives and the Lipschitz constants with respect to $ y $ of all the derivatives with respect to $ y $ of the $ ( r - 1) $- st derivatives, are bounded in $ \Pi _ {a} $; b) $ \inf B > 0 $; and c) the Gaussian curvature $ K $ is such that $ K = - B _ {xx} /B \leq - \beta ^ {2} = \textrm{ const } < 0 $. Then $ ds ^ {2} $ generates a Riemannian structure of class $ C ^ {r, 1 } $ on the manifold $ \Pi _ {a} $ with boundary, and the Riemannian space so obtained has an isometric immersion of class $ C ^ {r, 1 } $, $ r \geq 3 $, into $ E ^ {3} $. In particular, there exists an isometric immersion of any geodesic disc with an arbitrary (regular) metric of negative curvature. There is a number of theorems relating to isometric immersions of non-compact parts of metrics of negative curvature into $ E ^ {3} $[5]. Bounds have been given for the dimensions of the domains onto which a surface of negative (separated from zero) curvature has a one-to-one projection.

Since the metrics of type $ \Lambda $ are not globally immersible in $ E ^ {3} $, the problem of the isometric immersion of these metrics in Euclidean spaces of higher dimensions remains. There are only partial results in this direction; for example, there exists an isometric imbedding of class $ C ^ \infty $ of the Lobachevskii plane into $ E ^ {6} $ and an isometric immersion into $ E ^ {5} $; there is an example of a regular metric of type $ \Lambda $ having an isometric immersion into $ E ^ {4} $; however, it is not known if there is an isometric immersion of the Lobachevskii plane of class $ C ^ {r} , $ $ r \geq 2 $, into $ E ^ {4} $.

The question of the isometric immersibility into $ E ^ {3} $ of a metric with alternating curvature remains open, even in the local case. Thus, an example has been constructed [16] of a two-dimensional Riemannian manifold of class $ C ^ {2, 1 } $ not having a local isometric immersion of class $ C ^ {2, 1 } $ into $ E ^ {3} $. The problem of realizing an analytic metric with alternating curvature has been solved by the following theorem [17]: Suppose that the metric $ ds ^ {2} = dx ^ {2} + B ^ {2} ( x, y) dy ^ {2} $ is given on the rectangle $ \Pi _ {a, b } = \{ 0 \leq x \leq a, 0 \leq y \leq b \} $ in $ E ^ {2} $, and that $ B ( x, y) $ is an analytic function in some open rectangle containing $ \Pi _ {a, b } $; then the analytic Riemannian manifold with boundary generated by the given metric on $ \Pi _ {a, b } $ has an analytic isometric immersion into $ E ^ {3} $. There are a number of results concerning the isometric immersions of regular metrics of alternating curvature into Euclidean spaces of higher dimension (but close to three). Thus, if $ M ^ {2} $ is a complete Riemannian manifold of class $ C ^ {3, \alpha } $ which is homeomorphic to the plane, then each of its compact parts has an isometric immersion of class $ C ^ {2, \alpha } $ into $ E ^ {4} $; a Riemannian manifold homeomorphic to a torus also has an isometric immersion into $ E ^ {4} $. Every compact two-dimensional Riemannian manifold of class $ C ^ \infty $( $ C ^ \omega $) has an isometric immersion (and even an isometric imbedding) of class $ C ^ \infty $( $ C ^ \omega $) into $ E ^ {10} $. The two-dimensional sphere with any Riemannian metric of class $ C ^ \infty $ has an isometric immersion of class $ C ^ \infty $ into $ E ^ {7} $, and the Klein bottle and the Möbius strip have isometric immersions into $ E ^ {4} $.

If regularity of the immersion is dropped, then every two-dimensional Riemannian metric of class $ C ^ {r} $, $ r \geq 0 $, has an isometric immersion of class $ C ^ {1} $ into $ E ^ {3} $. However, in this case, the usual connections between the intrinsic and extrinsic geometries of the surface realizing the metric are violated. A local isometric immersion of a metric of the two-dimensional sphere as a locally non-convex surface of class $ C ^ {1, \alpha } $ into $ E ^ {3} $ has been constructed for any $ \alpha < 1/13 $, and an analogous global isometric immersion for any $ \alpha < 1/25 $. On the other hand, if the surface $ \Phi $ belongs to $ C ^ {1, \alpha } $, $ \alpha > 2/3 $, then $ \Phi $, having alternating interior curvature, must have bounded exterior curvature. In particular, if the interior curvature of $ \Phi $ is positive, then $ \Phi $ is a locally convex surface, and if in addition the metric of the surface is regular, then the surface itself is regular. Thus, the lower bound for the values of $ \alpha $ for which the connection between the intrinsic and extrinsic geometries of a surface $ \Phi $ of class $ C ^ {1, \alpha } $ with alternating interior curvature is preserved lies in the interval $ [ 1/13, 2/3] $. Finally, all orientable manifolds of bounded exterior curvatures not having points of curvature $ 2 \pi $ have isometric imbeddings into $ E ^ {3} $ as differentiable surfaces. In the investigation of non-regular isometric immersions, piecewise-linear isometric immersions of piecewise-linear metrics are also studied; thus, every evolute which is homeomorphic to a closed domain in an orientable closed surface can be isometrically imbedded as a polyhedron in $ E ^ {3} $.

References

[1]	N.V. Efimov, "Problems of global isometric imbedding" , Proc. 4-th All-Union Math. Congress , 1 , Leningrad (1963) pp. 86–99 (In Russian) MR0158336
[2]	I.Ya. Bakel'man, A.L. Verner, B.E. Kantor, "Introduction to differential geometry "in the large" " , Moscow (1973) (In Russian)
[3]	A.V. Pogorelov, "Extrinsic geometry of convex surfaces" , Amer. Math. Soc. (1973) (Translated from Russian) MR0346714 Zbl 0311.53067
[4]	A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian)
[5]	E.G. Poznyak, E.V. Shikin, "Surfaces of negative curvature" J. Soviet Math. , 5 (1976) pp. 865–887 Itogi Nauk. i Tekhn. Alg. Topol. Geom. , 12 (1974) pp. 171–207 Zbl 0107.15502
[6]	J. Nash, "The imbedding theorem for Riemannian manifolds" Ann. of Math. (2) , 63 (1956) pp. 20–63
[7]	M.L. Gromov, V.A. Rokhlin, "Embeddings and immersions in Riemannian geometry" Russian Math. Surveys , 25 : 5 (1970) pp. 1–57 Uspekhi Mat. Nauk , 25 : 5 (1970) pp. 3–62 Zbl 0222.53053 Zbl 0202.21004
[8]	I.Kh. Sabitov, S.Z. Shevel', "The connections between the order of smoothness of a surface and its metric" Siberian Math. J. , 17 : 4 (1977) pp. 687–693 Sibirsk. Mat. Zh. , 17 : 4 (1976) pp. 916–925 Zbl 0386.53014
[9]	T. Ôtsuki, "Isometric imbedding of Riemann manifolds in a Riemann manifold" J. Math. Soc. Japan , 6 (1954) pp. 221–234 MR0067550 Zbl 0058.37702
[10]	J. Nash, "Analyticity of the solutions of implicit function problems with analytic data" Ann. of Math. , 84 (1966) pp. 345–355 MR0205266 Zbl 0173.09202
[11]	N.A. Rozenson, "Sur les espaces de Riemanniens de classe I, III" Izv. Akad. Nauk SSSR Ser. Mat. , 7 (1943) pp. 253–284 (In Russian) (French summary)
[12]	A. Friedman, "Local isometric imbedding of Riemannian manifolds with indefinite metrics" J. Math. Mech. , 10 (1961) pp. 625–649 MR0125544 Zbl 0187.19103
[13]	I.Kh. Sabitov, "The regularity of convex regions with a metric that is regular in the Hölder classes" Siberian Math. J. , 17 : 4 (1977) pp. 681–686 Sibirsk. Mat. Zh. , 17 : 4 (1976) pp. 907–915 Zbl 0386.53041
[14]	N.V. Efimov, "Generation of singularities on surfaces of negative curvature" Mat. Sb. , 64 : 2 (1964) pp. 286–320 (In Russian)
[15]	E.G. Poznyak, "Regular global realizations of two-dimensional metrics with negative curvature" Ukr. Geom. Sb. : 3 (1966) pp. 78–92 (In Russian)
[16]	A.V. Pogorelov, "An example of a two-dimensional Riemannian metric admitting no local realization in 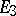" Soviet Math. Izv. , 12 : 3 (1971) pp. 729–730 Dokl. Akad. Nauk SSSR , 198 : 1 (1971) pp. 42–43
[17]	E.G. Poznyak, "Isometric immersions of two-dimensional Riemannian metrics in Euclidean space" Russian Math. Surveys , 28 : 4 (1973) pp. 47–77 Uspekhi Mat. Nauk , 28 : 4 (1973) pp. 47–76 Zbl 0289.53004
[18]	Yu.D. Burago, V.A. Zalgaller, "Polyhedral imbedding of nets" Vestnik Leningrad. Univ. Ser. Mat. Mekh. Astron. , 15 : 7 (1960) pp. 66–80 (In Russian) (English summary)

Comments

For global isometric immersions see also [a1]. This reference contains, in general, better estimates than those given in the main article above. E.g., a Riemannian manifold $ M ^ {k} $ of class $ C ^ {r} $ has an isometric imbedding of class $ C ^ {r} $( $ 3 \leq r \leq \infty $):

into every ball in $ E ^ {n} $ for $ n \leq 3 k ( k + 9 ) / 2 $ if $ M ^ {k} $ is compact;

into every part of $ E ^ {n} $ for $ n \leq 3 k ( k+ 1) ( k+ 9) / 2 $ if $ M ^ {k} $ is not compact.

A $ k $- dimensional hyperbolic space can be $ C ^ \infty $ isometrically imbedded into $ E ^ {4 k - 3 } $.

Concerning the statements involving homotopy (last section of "global isometric immersions" above) see also [a2].

For the fact that $ C ^ {r} $ isometric immersions ( $ r \geq 3 $, $ r = a $) into $ V ^ {3} $ can be joined by a deformation of transformations in the same class see [a3].

In the West an isometric imbedding is usually understood to a mean a one-to-one immersion (as in the main article) satisfying the additional requirement that the topology induced by the injective immersion coincides with the given topology on the domain manifold.

References

[a1]	M. Gromov, "Partial differential relations" , Springer (1986) (Translated from Russian) MR0864505 Zbl 0651.53001
[a2]	N. Kuiper, "On 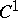-isometric imbedding, I" Proc. K. Ned. Akad. Wetensch. , A-58 (1955) pp. 545–556 MR75640
[a3]	L. Nirenberg, "The Weyl and Minkowski problems in differential geometry in the large" Comm. Pure Appl. Math. , 6 (1953) pp. 337–394 MR0058265 Zbl 0051.12402