Convex metric
An internal metric on a two-dimensional manifold  which meets some convexity condition. More exactly, let
which meets some convexity condition. More exactly, let 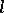 and
and 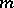 be two shortest lines issuing from some point
be two shortest lines issuing from some point  ; let
; let 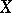 and
and 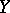 be points on these lines; let
be points on these lines; let  be the distances from
be the distances from 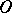 to
to  and
and 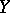 , respectively; let
, respectively; let  be the distance between
be the distance between 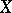 and
and 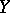 ; and let
; and let 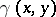 be the angle opposite to the side
be the angle opposite to the side  in the plane triangle with sides
in the plane triangle with sides 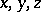 . The convexity condition of the metric (at the point
. The convexity condition of the metric (at the point 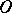 ) is that
) is that 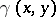 is a non-increasing function (i.e.
is a non-increasing function (i.e. 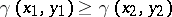 if
if 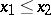 ,
,  ) on any pair of intervals
) on any pair of intervals 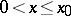 ,
, 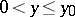 such that the points
such that the points 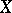 and
and 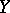 , which correspond to two arbitrary values in these intervals, can be connected by a shortest line. An internal metric is a convex metric if and only if it is a metric of non-negative curvature. The metric of a convex surface is a convex metric. Conversely, any two-dimensional manifold with a convex metric can be realized as a convex surface (Aleksandrov's theorem).
, which correspond to two arbitrary values in these intervals, can be connected by a shortest line. An internal metric is a convex metric if and only if it is a metric of non-negative curvature. The metric of a convex surface is a convex metric. Conversely, any two-dimensional manifold with a convex metric can be realized as a convex surface (Aleksandrov's theorem).
References
| [1] | A.D. Aleksandrov, "Die innere Geometrie der konvexen Flächen" , Akademie Verlag (1955) (Translated from Russian) |
Convex metric. M.I. Voitsekhovskii (originator), Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Convex_metric&oldid=12734