Difference between revisions of "P-space"
(Explanatory header) |
m (more latex conversion) |
||
| Line 10: | Line 10: | ||
One also employs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002037.png" />-spaces in the investigation of [[box product]]s [[#References|[a7]]]. If a product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002038.png" /> is endowed with the box topology, then the equivalence relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002039.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002040.png" /> being finite defines a quotient space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002041.png" />, denoted <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002042.png" />, that is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002043.png" />-space. The quotient mapping is open and the box product and its quotient share many properties. | One also employs <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002037.png" />-spaces in the investigation of [[box product]]s [[#References|[a7]]]. If a product <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002038.png" /> is endowed with the box topology, then the equivalence relation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002039.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002040.png" /> being finite defines a quotient space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002041.png" />, denoted <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002042.png" />, that is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002043.png" />-space. The quotient mapping is open and the box product and its quotient share many properties. | ||
| − | == | + | ==$P$-space in the sense of Morita.== |
| − | A | + | A $P$-space as defined in [[#References|[a3]]] is a [[Topological space|topological space]] $X$ with the following covering property: Let $\Omega$ be a set and let $\{G(\alpha_1, \dots,\alpha_n): \alpha_1, \dots,\alpha_n \in \Omega\}$ be a family of open sets (indexed by the set of finite sequences of elements of $\Omega$). Then there is a family $\{F(\alpha_1, \dots,\alpha_n): \alpha_1, \dots,\alpha_n \in \Omega\}$ of closed sets such that $F(\alpha_1, \dots,\alpha_n) \subseteq G(\alpha_1, \dots,\alpha_n)$ and whenever a sequence $(\alpha_i)_{i=1}^{\infty}$ satisfies <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002053.png" />, then also <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002054.png" />. K. Morita introduced $P$-spaces to characterize spaces whose products with all metrizable spaces are normal (cf. also [[Normal space|Normal space]]): A space is a normal (paracompact) $P$-space if and only if its product with every [[Metrizable space|metrizable space]] is normal (paracompact, cf. also [[Paracompact space|Paracompact space]]). |
| − | Morita [[#References|[a4]]] conjectured that this characterization is symmetric in that a space is metrizable if and only if its product with every normal | + | Morita [[#References|[a4]]] conjectured that this characterization is symmetric in that a space is metrizable if and only if its product with every normal $P$-space is normal. K. Chiba, T.C. Przymusiński and M.E. Rudin [[#References|[a1]]] showed that the conjecture is true if $V=L$, ''i.e.'' Gödel's [[axiom of constructibility]], holds (cf. also [[Gödel constructive set|Gödel constructive set]]). These authors also showed that another conjecture of Morita is true without any extra set-theoretic axioms: If $X \times Y$ is normal for every normal space $Y$, then $X$ is discrete: cf. [[Morita conjectures]]. |
| − | There is a characterization of | + | There is a characterization of $P$-spaces in terms of topological games [[#References|[a6]]]; let two players, I and II, play the following game on a topological space: player I chooses open sets $U_1,U_2,\dots$ and player II chooses closed sets $F_1,F_2,\dots$, with the proviso that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p130/p130020/p13002065.png" />. Player II wins the play if $\bigcup_n F_n = X$. One can show that Player II has a winning strategy if and only if $X$ is a $P$-space. |
==$p$-space in the sense of Arkhangel'skii.== | ==$p$-space in the sense of Arkhangel'skii.== | ||
Revision as of 12:49, 19 March 2023
$P$-space or $p$-space refers to various classes of topological space, discussed below.
PSPACE or $\mathcal{P}$-space refers to an algorithmic complexity class.
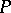 -space in the sense of Gillman–Henriksen.
-space in the sense of Gillman–Henriksen.
A 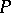 -space as defined in [a2] is a completely-regular space in which every point is a
-space as defined in [a2] is a completely-regular space in which every point is a  -point, i.e., every fixed prime ideal in the ring
-point, i.e., every fixed prime ideal in the ring  of real-valued continuous functions is maximal (cf. also Maximal ideal; Prime ideal); this is equivalent to saying that every
of real-valued continuous functions is maximal (cf. also Maximal ideal; Prime ideal); this is equivalent to saying that every  -subset is open (cf. also Set of type
-subset is open (cf. also Set of type  (
(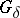 )). The latter condition is used to define
)). The latter condition is used to define  -spaces among general topological spaces. In [a5] these spaces were called
-spaces among general topological spaces. In [a5] these spaces were called 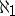 -additive, because countable unions of closed sets are closed.
-additive, because countable unions of closed sets are closed.
Non-Archimedean ordered fields are 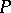 -spaces, in their order topology; thus,
-spaces, in their order topology; thus,  -spaces occur in non-standard analysis. Another source of
-spaces occur in non-standard analysis. Another source of 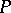 -spaces is formed by the
-spaces is formed by the 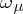 -metrizable spaces of [a5]. If
-metrizable spaces of [a5]. If  is a regular cardinal number (cf. also Cardinal number), then an
is a regular cardinal number (cf. also Cardinal number), then an  -metrizable space is a set
-metrizable space is a set  with a mapping
with a mapping 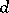 from
from 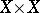 to the ordinal
to the ordinal  that acts like a metric:
that acts like a metric:  if and only if
if and only if 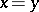 ;
; 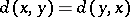 and
and  ;
; 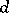 is called an
is called an 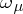 -metric. A topology is formed, as for a metric space, using
-metric. A topology is formed, as for a metric space, using  -balls:
-balls: 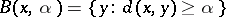 , where
, where  . The
. The  -metrizable spaces are exactly the strongly zero-dimensional metric spaces [a8] (cf. also Zero-dimensional space). If
-metrizable spaces are exactly the strongly zero-dimensional metric spaces [a8] (cf. also Zero-dimensional space). If  is uncountable, then
is uncountable, then 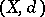 is a
is a 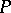 -space (and conversely).
-space (and conversely).
One also employs  -spaces in the investigation of box products [a7]. If a product
-spaces in the investigation of box products [a7]. If a product  is endowed with the box topology, then the equivalence relation
is endowed with the box topology, then the equivalence relation  defined by
defined by  being finite defines a quotient space of
being finite defines a quotient space of  , denoted
, denoted 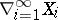 , that is a
, that is a 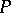 -space. The quotient mapping is open and the box product and its quotient share many properties.
-space. The quotient mapping is open and the box product and its quotient share many properties.
$P$-space in the sense of Morita.
A $P$-space as defined in [a3] is a topological space $X$ with the following covering property: Let $\Omega$ be a set and let $\{G(\alpha_1, \dots,\alpha_n): \alpha_1, \dots,\alpha_n \in \Omega\}$ be a family of open sets (indexed by the set of finite sequences of elements of $\Omega$). Then there is a family $\{F(\alpha_1, \dots,\alpha_n): \alpha_1, \dots,\alpha_n \in \Omega\}$ of closed sets such that $F(\alpha_1, \dots,\alpha_n) \subseteq G(\alpha_1, \dots,\alpha_n)$ and whenever a sequence $(\alpha_i)_{i=1}^{\infty}$ satisfies 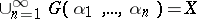 , then also
, then also 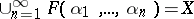 . K. Morita introduced $P$-spaces to characterize spaces whose products with all metrizable spaces are normal (cf. also Normal space): A space is a normal (paracompact) $P$-space if and only if its product with every metrizable space is normal (paracompact, cf. also Paracompact space).
. K. Morita introduced $P$-spaces to characterize spaces whose products with all metrizable spaces are normal (cf. also Normal space): A space is a normal (paracompact) $P$-space if and only if its product with every metrizable space is normal (paracompact, cf. also Paracompact space).
Morita [a4] conjectured that this characterization is symmetric in that a space is metrizable if and only if its product with every normal $P$-space is normal. K. Chiba, T.C. Przymusiński and M.E. Rudin [a1] showed that the conjecture is true if $V=L$, i.e. Gödel's axiom of constructibility, holds (cf. also Gödel constructive set). These authors also showed that another conjecture of Morita is true without any extra set-theoretic axioms: If $X \times Y$ is normal for every normal space $Y$, then $X$ is discrete: cf. Morita conjectures.
There is a characterization of $P$-spaces in terms of topological games [a6]; let two players, I and II, play the following game on a topological space: player I chooses open sets $U_1,U_2,\dots$ and player II chooses closed sets $F_1,F_2,\dots$, with the proviso that 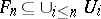 . Player II wins the play if $\bigcup_n F_n = X$. One can show that Player II has a winning strategy if and only if $X$ is a $P$-space.
. Player II wins the play if $\bigcup_n F_n = X$. One can show that Player II has a winning strategy if and only if $X$ is a $P$-space.
$p$-space in the sense of Arkhangel'skii.
A feathered space or plumed space, a completely-regular Hausdorff space having a feathering in some Hausdorff compactification, has been termed a $p$-space. For paracompact spaces these coincide with the $p$-spaces of Morita, [b1].
References
| [a1] | K. Chiba, T.C. Przymusiński, M.E. Rudin, "Normality of products and Morita's conjectures" Topol. Appl. , 22 (1986) pp. 19–32 |
| [a2] | L. Gillman, M. Henriksen, "Concerning rings of continuous functions" Trans. Amer. Math. Soc. , 77 (1954) pp. 340–362 |
| [a3] | K. Morita, "Products of normal spaces with metric spaces" Math. Ann. , 154 (1964) pp. 365–382 |
| [a4] | K. Morita, "Some problems on normality of products of spaces" J. Novák (ed.) , Proc. Fourth Prague Topological Symp. (Prague, August 1976) , Soc. Czech. Math. and Physicists , Prague (1977) pp. 296–297 (Part B: Contributed papers) |
| [a5] | R. Sikorski, "Remarks on some topological spaces of high power" Fundam. Math. , 37 (1950) pp. 125–136 |
| [a6] | R. Telgárski, "A characterization of $P$-spaces" Proc. Japan Acad. , 51 (1975) pp. 802–807 |
| [a7] | S.W. Williams, "Box products" K. Kunen (ed.) J.E. Vaughan (ed.) , Handbook of Set Theoretic Topology , North-Holland (1984) pp. Chap. 4; 169–200 |
| [a8] | J. de Groot, "Non-Archimedean metrics in topology" Proc. Amer. Math. Soc. , 7 (1956) pp. 948–953 |
| [b1] | J.-I. Nagata, "Modern general topology" , North-Holland (1985) |
P-space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=P-space&oldid=52977