Difference between revisions of "Chern class"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | c0220301.png | ||
| + | $#A+1 = 134 n = 1 | ||
| + | $#C+1 = 134 : ~/encyclopedia/old_files/data/C022/C.0202030 Chern class | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | A [[Characteristic class|characteristic class]] defined for complex vector bundles. A Chern class of the complex vector bundle $ \xi $ | |
| + | over a base $ B $ | ||
| + | is denoted by $ c _ {i} ( \xi ) \in H ^ {2i} ( B) $ | ||
| + | and is defined for all natural indices $ i $. | ||
| + | By the complete Chern class is meant the inhomogeneous characteristic class $ 1 + c _ {1} + c _ {2} + \dots $, | ||
| + | and the Chern polynomial is the expression $ c _ {t} = 1 + c _ {1} t + c _ {2} t ^ {2} + \dots $, | ||
| + | where $ t $ | ||
| + | is a formal unknown. Chern classes were introduced in [[#References|[1]]]. | ||
| − | + | The characteristic classes, defined for all $ n $- | |
| + | dimensional complex vector bundles and with values in the integral cohomology, are naturally identified with the elements of the ring $ H ^ {**} ( \mathop{\rm BU} _ {n} ) $. | ||
| + | In this sense the Chern classes $ c _ {i} $ | ||
| + | can be thought of as elements of the groups $ H ^ {2i} ( \mathop{\rm BU} _ {n} ) $, | ||
| + | the complete Chern class as an element of the ring $ H ^ {**} ( \mathop{\rm BU} _ {n} ) $, | ||
| + | and the Chern polynomial as an element of the formal power series ring $ H ^ {**} ( \mathop{\rm BU} _ {n} ) [ [ t ] ] $. | ||
| − | + | The Chern classes satisfy the following properties, which uniquely determine them. 1) For two vector bundles $ \xi , \eta $ | |
| + | with a common base $ B $, | ||
| + | $ c ( \xi \oplus \eta ) = c ( \xi ) c ( \eta ) $, | ||
| + | in other words $ c _ {k} ( \xi \oplus \eta ) = \sum _ {i} c _ {i} ( \xi ) c _ {k-} i ( \eta ) $ | ||
| + | where $ c _ {0} = 1 $. | ||
| + | 2) For the one-dimensional universal bundle $ \kappa _ {1} $ | ||
| + | over $ \mathbf C P ^ \infty $ | ||
| + | the identity $ c ( \kappa _ {1} ) = 1 + u $ | ||
| + | holds, where $ u \in H ^ {2} ( \mathbf C P ^ \infty ) $ | ||
| + | is the orientation of $ \kappa _ {1} $( | ||
| + | $ \mathbf C P ^ \infty $ | ||
| + | is the [[Thom space|Thom space]] of $ \kappa _ {1} $, | ||
| + | which, being complex, has a uniquely-defined orientation $ u $). | ||
| − | + | Consequences of the properties 1)–2) are: $ c _ {i} ( \xi ) = 0 $ | |
| + | for $ i > \mathop{\rm dim} \xi $, | ||
| + | and $ c ( \xi ) = c ( \xi \oplus \theta ) $, | ||
| + | where $ \theta $ | ||
| + | is the trivial bundle. The latter fact allows one to define Chern classes as elements of the ring $ H ^ {**} ( \mathop{\rm BU} ) $. | ||
| − | + | If $ \omega = \{ i _ {1} \dots i _ {k} \} $ | |
| + | is a collection of non-negative integers, then $ c _ \omega $ | ||
| + | denotes the characteristic class $ c _ {i _ {1} } \dots c _ {i _ {k} } \in H ^ {2n} ( \mathop{\rm BU} ) $, | ||
| + | where $ n = i _ {1} + \dots + i _ {k} $. | ||
| − | + | Under the natural monomorphism $ H ^ {**} ( \mathop{\rm BU} _ {n} ) \rightarrow H ^ {**} ( \mathop{\rm BT} _ {n} ) = \mathbf Z [ [ x _ {1} \dots x _ {n} ] ] $ | |
| + | induced by the mapping $ \mathop{\rm BT} _ {n} = \mathbf C P ^ \infty \times \dots \times \mathbf C P ^ \infty \rightarrow \mathop{\rm BU} _ {n} $, | ||
| + | the Chern classes are mapped into the elementary symmetric functions, and the complete Chern class is mapped to the polynomial $ \prod _ {i=} 1 ^ {n} ( 1 + x _ {i} ) $. | ||
| + | The image of the ring $ H ^ {**} ( \mathop{\rm BU} _ {n} ) $ | ||
| + | in $ H ^ {**} ( \mathop{\rm BT} _ {n} ) = \mathbf Z [ [ x _ {1} \dots x _ {n} ] ] $ | ||
| + | is the subring consisting of all symmetric formal power series. Every symmetric formal power series in the Wu generators $ x _ {1} \dots x _ {n} $ | ||
| + | determines a characteristic class that can be expressed in terms of Chern classes. For example, the series $ \prod _ {i=} 1 ^ {n} x _ {i} / ( 1 - e ^ {x _ {i} } ) $ | ||
| + | determines a characteristic class with rational coefficients, called the Todd class and denoted by $ T \in H ^ {**} ( \mathop{\rm BU} _ {n} ; \mathbf Q ) $. | ||
| − | + | Let $ \omega = \{ i _ {1} \dots i _ {k} \} $ | |
| + | be a set of non-negative integers. Let $ S _ \omega ( c _ {1} \dots c _ {n} ) $ | ||
| + | denote the characteristic class defined by the smallest symmetric polynomial in the variables $ x _ {1} \dots x _ {n} $, | ||
| + | where $ n \geq i _ {1} + \dots + i _ {k} $, | ||
| + | containing the monomial $ x _ {1} ^ {i _ {1} } \dots x _ {k} ^ {i _ {k} } $. | ||
| − | + | Let $ h ^ {*} $ | |
| + | be an oriented multiplicative cohomology theory. Then the Chern classes $ \sigma _ {i} $ | ||
| + | with values in $ h ^ {*} $ | ||
| + | satisfy, as do ordinary Chern classes, the properties: $ \sigma ( \xi \oplus \eta ) = \sigma ( \xi ) \sigma ( \eta ) $, | ||
| + | $ \sigma = 1 + \sigma _ {1} + \sigma _ {2} + \dots $, | ||
| + | $ \sigma ( \kappa _ {1} ) = 1 + u \in h ^ {*} ( \mathbf C P ^ \infty ) $, | ||
| + | where $ u \in h ^ {2} ( \mathbf C P ^ \infty ) $ | ||
| + | is the orientation of the bundle $ \kappa _ {1} $, | ||
| + | and these properties completely determine them. As with ordinary Chern classes, one uses the notation $ \sigma _ \omega = \sigma _ {i _ {1} } \dots \sigma _ {i _ {k} } $ | ||
| + | and $ S _ \omega ( \sigma _ {1} \dots \sigma _ {n} ) $. | ||
| + | If $ \xi , \eta $ | ||
| + | are two complex vector bundles, then | ||
| − | + | $$ | |
| + | S _ \omega ( \sigma _ {1} \dots \sigma _ {n} ) ( \xi \oplus \eta ) = | ||
| + | $$ | ||
| − | + | $$ | |
| + | = \ | ||
| + | \sum _ {\omega ^ \prime \cup \omega ^ {\prime\prime} = \omega } S _ { | ||
| + | \omega ^ \prime } ( \sigma _ {1} \dots \sigma _ {n} ) ( \xi ) S _ {\omega ^ {\prime\prime} } ( \sigma _ {1} \dots \sigma _ {n} ) ( \eta ) , | ||
| + | $$ | ||
| − | + | where the summation is taken over all sets $ \omega ^ \prime , \omega ^ {\prime\prime} $ | |
| + | with $ \omega ^ \prime \cup \omega ^ {\prime\prime} = \omega $. | ||
| − | + | In place of the theory $ h ^ {*} $ | |
| + | one may take a unitary [[Cobordism|cobordism]] theory $ U ^ {*} $ | ||
| + | or [[K-theory| $ K $- | ||
| + | theory]]. For a $ U ^ {*} $- | ||
| + | theory the element $ u \in U ^ {2} ( \mathbf C P ^ \infty ) $ | ||
| + | is defined by the identity mapping $ \mathbf C P ^ \infty \rightarrow \mathbf C P ^ \infty = \mathop{\rm MU} _ {1} $, | ||
| + | and for $ K $- | ||
| + | theory $ u = \beta ( 1 - [ \overline{x}\; ] ) \in \widetilde{K} {} ^ {2} ( \mathbf C P ^ \infty ) $, | ||
| + | where $ \widetilde \beta : K ^ {0} \rightarrow K ^ {2} $ | ||
| + | is the Bott periodicity operator. The notation $ \sigma _ {i} $ | ||
| + | is retained for Chern classes with values in a $ U ^ {*} $- | ||
| + | theory, while Chern classes with values in $ K $- | ||
| + | theory are denoted by $ \gamma _ {i} $. | ||
| − | + | According to the general theory, $ \gamma _ {i} ( \xi ) \in K ^ {2i} ( B) $, | |
| + | where $ \xi $ | ||
| + | is a vector bundle with base $ B $. | ||
| + | However $ K $- | ||
| + | theory is often conveniently thought of as a $ \mathbf Z _ {2} $- | ||
| + | graded theory, identifying the groups $ K ^ {n} ( B) $ | ||
| + | and $ K ^ {n+} 2 ( B) $ | ||
| + | via the periodicity operator $ \beta $. | ||
| + | Then $ K ^ {*} ( B) = K ^ {0} ( B) \oplus K ^ {1} ( B) $ | ||
| + | and $ \gamma ( \xi ) \in K ^ {0} ( B) $ | ||
| + | for all $ i $. | ||
| + | From this point of view it makes sense to consider, instead of the complete Chern class, the Chern polynomial | ||
| − | + | $$ | |
| + | \gamma _ {t} ( \xi ) = 1 + \sum _ {i > 0 } | ||
| + | \gamma _ {i} ( \xi ) t ^ {i} \in K ^ {0} ( B) [ t] . | ||
| + | $$ | ||
| − | + | Let $ \lambda ^ {i} ( \xi ) = [ \xi \wedge \dots \wedge \xi ] $ | |
| + | be a cohomology operation in $ K $- | ||
| + | theory ( $ i $ | ||
| + | terms). The polynomial | ||
| − | + | $$ | |
| + | \lambda _ {t} ( \xi ) = \sum _ { i= } 0 ^ \infty | ||
| + | \lambda ^ {i} ( \xi ) t ^ {i} \in K ^ {0} ( B) [ t] | ||
| + | $$ | ||
| + | |||
| + | satisfies, as does $ \gamma _ {t} $, | ||
| + | the multiplicative property | ||
| + | |||
| + | $$ | ||
| + | \lambda _ {t} ( \xi \oplus \eta ) = \ | ||
| + | \lambda _ {t} ( \xi ) \lambda _ {t} ( \eta ) . | ||
| + | $$ | ||
There is the following connection between these polynomials: | There is the following connection between these polynomials: | ||
| − | + | $$ | |
| + | |||
| + | \frac{\lambda _ {t} }{1-} | ||
| + | t ( \overline \xi \; - \mathop{\rm dim} \xi ) = 1 + | ||
| + | \sum _ { i= } 1 ^ \infty (- 1) \gamma _ {i} ( \xi ) t ^ {i} = \ | ||
| + | \gamma _ {-} t ( \xi ) . | ||
| + | $$ | ||
| − | Here both parts of the equation lie in | + | Here both parts of the equation lie in $ K ^ {0} ( B) [ t] $ |
| + | and $ \xi $ | ||
| + | is the trivial bundle of dimension $ \mathop{\rm dim} \xi $. | ||
| + | The classes $ \gamma _ {i} $ | ||
| + | in this construction are different from those constructed by M.F. Atiyah, who defined them by the formula $ \gamma _ {t} ( \xi ) = ( \lambda _ {t} / ( 1 - t ) ) ( \xi ) $. | ||
| + | R. Stong [[#References|[2]]] defined classes $ \gamma _ {i} $ | ||
| + | that satisfy the condition | ||
| − | + | $$ | |
| + | \gamma _ {t} ( \xi ) = | ||
| + | \frac{\lambda _ {t} }{1-} | ||
| + | t | ||
| + | ( \overline \xi \; - \mathop{\rm dim} \xi ) . | ||
| + | $$ | ||
The difference arises because, for Stong, | The difference arises because, for Stong, | ||
| − | + | $$ | |
| + | u = \beta ( [ \kappa _ {1} ] - 1 ) \in \ | ||
| + | \widetilde{K} {} ^ {2} ( \mathbf C P ^ \infty ) . | ||
| + | $$ | ||
| + | |||
| + | The classes $ \sigma _ {i} $ | ||
| + | are connected with the notion of a Landweber–Novikov algebra, which is very fruitful in homotopy theory. For an arbitrary set $ \omega = \{ i _ {1} \dots i _ {k} \} $ | ||
| + | of non-negative integers, consider the characteristic class $ S _ \omega ( \sigma _ {1} \dots \sigma _ {n} ) \in U ^ {2d} ( \mathop{\rm BU} ) $, | ||
| + | where $ d = i _ {1} + \dots + i _ {k} $. | ||
| + | There is a [[Thom isomorphism|Thom isomorphism]] $ U ^ {2d} ( \mathop{\rm BU} ) \rightarrow \widetilde{U} {} ^ {2d} ( \mathop{\rm MU} ) \subset U ^ {2d} ( \mathop{\rm MU} ) $, | ||
| + | where $ \mathop{\rm MU} $ | ||
| + | is the spectrum corresponding to the $ U ^ {*} $- | ||
| + | theory. The image of the class $ S _ \omega ( \sigma _ {1} \dots \sigma _ {n} ) $ | ||
| + | in $ U ^ {2d} ( \mathop{\rm MU} ) $ | ||
| + | determines a [[Cohomology operation|cohomology operation]] in the $ U ^ {*} $- | ||
| + | theory. The subalgebra of the [[Steenrod algebra|Steenrod algebra]] in the $ U ^ {*} $- | ||
| + | theory generated by the operations of this form is called the Landweber–Novikov algebra. The operation constructed from the set $ \omega = \{ i _ {1} \dots i _ {k} \} $ | ||
| + | is denoted by $ S _ \omega $. | ||
| − | + | For one-dimensional bundles $ \xi , \eta $ | |
| + | there is the identity | ||
| − | + | $$ | |
| + | c _ {1} ( \xi \otimes \eta ) = c _ {1} ( \xi ) + c _ {1} ( \eta ) . | ||
| + | $$ | ||
| − | + | This important property, which enables one to define the [[Chern character|Chern character]], does not hold in generalized cohomology theories. However there exists a formal power series $ g ( t) $ | |
| + | with coefficients in $ h ^ {*} ( \mathop{\rm pt} ) \otimes \mathbf Q $, | ||
| + | such that $ g ( \sigma _ {1} ( \xi \otimes \eta )) = g ( \sigma _ {1} ( \xi ) ) + g ( \sigma _ {1} ( \eta ) ) $, | ||
| + | where $ \sigma _ {1} $ | ||
| + | is the first Chern class with coefficients in $ h ^ {*} $. | ||
| + | For the unitary cobordism theory | ||
| − | + | $$ | |
| + | g ( t) = \sum _ { n= } 0 ^ \infty | ||
| − | + | \frac{[ \mathbf C P ^ {n} ] }{n+} | |
| + | 1 t ^ {n+} 1 , | ||
| + | $$ | ||
| − | where | + | where $ [ \mathbf C P ^ {n} ] = \Omega _ {u} ^ {*} = U ^ {*} ( \mathop{\rm pt} ) $ |
| + | is the cobordism class of the projective space $ \mathbf C P ^ {n} $. | ||
| + | This series is called the Mishchenko series. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.S. Chern, "Characteristic classes of Hermitian manifolds" ''Ann. of Math.'' , '''47''' : 1 (1946) pp. 85–121 {{MR|0015793}} {{ZBL|0060.41416}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) {{MR|0248858}} {{ZBL|0181.26604}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965) {{MR|0198494}} {{ZBL|0137.17002}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) {{MR|0176478}} {{ZBL|0125.40103}} </TD></TR><TR><TD valign="top">[5a]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" ''Ann. of Math. (2)'' , '''87''' (1968) pp. 484–530 {{MR|0236950}} {{MR|0232402}} {{ZBL|0164.24001}} </TD></TR><TR><TD valign="top">[5b]</TD> <TD valign="top"> M.F. Atiyah, G.B. Segal, "The index of elliptic operators II" ''Ann. of Math. (2)'' , '''87''' (1968) pp. 531–545 {{MR|0236953}} {{MR|0236951}} {{ZBL|0164.24201}} </TD></TR><TR><TD valign="top">[5c]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators III" ''Ann. of Math. (2)'' , '''87''' (1968) pp. 546–604 {{MR|0236952}} {{ZBL|0164.24301}} </TD></TR><TR><TD valign="top">[5d]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators IV" ''Ann. of Math. (2)'' , '''93''' (1971) pp. 119–138 {{MR|0279833}} {{ZBL|0212.28603}} </TD></TR><TR><TD valign="top">[5e]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators V" ''Ann. of Math. (2)'' , '''93''' (1971) pp. 139–149 {{MR|0279834}} {{ZBL|0212.28603}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) {{MR|1335917}} {{MR|0202713}} {{ZBL|0376.14001}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) {{MR|0229247}} {{ZBL|0144.44804}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.M. Bukhshtaber, "The Chern–Dold character in cobordisms" ''Math. USSR-Sb.'' , '''12''' : 4 (1970) pp. 573–594 ''Mat. Sb.'' , '''83''' (1970) pp. 575–595 {{MR|}} {{ZBL|0219.57027}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> S.P. Novikov, "The method of algebraic topology from the viewpoint of cobordism theory" ''Math. USSR-Izv.'' , '''4''' : 1 (1967) pp. 827–913 ''Izv. Akad. SSSR Ser. Mat.'' , '''31''' : 4 (1967) pp. 855–951</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022030/c022030127.png" />-theory: lectures" , Benjamin (1967) {{MR|224083}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S.S. Chern, "Characteristic classes of Hermitian manifolds" ''Ann. of Math.'' , '''47''' : 1 (1946) pp. 85–121 {{MR|0015793}} {{ZBL|0060.41416}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) {{MR|0248858}} {{ZBL|0181.26604}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965) {{MR|0198494}} {{ZBL|0137.17002}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) {{MR|0176478}} {{ZBL|0125.40103}} </TD></TR><TR><TD valign="top">[5a]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" ''Ann. of Math. (2)'' , '''87''' (1968) pp. 484–530 {{MR|0236950}} {{MR|0232402}} {{ZBL|0164.24001}} </TD></TR><TR><TD valign="top">[5b]</TD> <TD valign="top"> M.F. Atiyah, G.B. Segal, "The index of elliptic operators II" ''Ann. of Math. (2)'' , '''87''' (1968) pp. 531–545 {{MR|0236953}} {{MR|0236951}} {{ZBL|0164.24201}} </TD></TR><TR><TD valign="top">[5c]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators III" ''Ann. of Math. (2)'' , '''87''' (1968) pp. 546–604 {{MR|0236952}} {{ZBL|0164.24301}} </TD></TR><TR><TD valign="top">[5d]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators IV" ''Ann. of Math. (2)'' , '''93''' (1971) pp. 119–138 {{MR|0279833}} {{ZBL|0212.28603}} </TD></TR><TR><TD valign="top">[5e]</TD> <TD valign="top"> M.F. Atiyah, I.M. Singer, "The index of elliptic operators V" ''Ann. of Math. (2)'' , '''93''' (1971) pp. 139–149 {{MR|0279834}} {{ZBL|0212.28603}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) {{MR|1335917}} {{MR|0202713}} {{ZBL|0376.14001}} </TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) {{MR|0229247}} {{ZBL|0144.44804}} </TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> V.M. Bukhshtaber, "The Chern–Dold character in cobordisms" ''Math. USSR-Sb.'' , '''12''' : 4 (1970) pp. 573–594 ''Mat. Sb.'' , '''83''' (1970) pp. 575–595 {{MR|}} {{ZBL|0219.57027}} </TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> S.P. Novikov, "The method of algebraic topology from the viewpoint of cobordism theory" ''Math. USSR-Izv.'' , '''4''' : 1 (1967) pp. 827–913 ''Izv. Akad. SSSR Ser. Mat.'' , '''31''' : 4 (1967) pp. 855–951</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c022/c022030/c022030127.png" />-theory: lectures" , Benjamin (1967) {{MR|224083}} {{ZBL|}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | + | $ H ^ {**} ( X) $ | |
| + | denotes the completion $ \prod _ {i \geq 0 } H ^ {i} ( X) $ | ||
| + | of $ H ^ {*} ( X) = \oplus _ {i \geq 0 } H ^ {i} ( X) $. | ||
| − | The power series | + | The power series $ g ( t) \in h ^ {*} ( \mathop{\rm pt} ) \otimes \mathbf Q $ |
| + | for a complex oriented cohomology theory $ h ^ {*} $ | ||
| + | such that $ g ( \sigma _ {1} ( \xi \otimes \eta ) ) = g ( \sigma _ {1} ( \xi ) ) + g ( \sigma _ {1} ( \eta ) ) $ | ||
| + | is the logarithm of the formal group $ F _ {h} ( X , Y ) $ | ||
| + | defined by $ h ^ {*} $; | ||
| + | cf. [[Cobordism|Cobordism]] and [[Formal group|Formal group]] for some more details. | ||
Revision as of 16:43, 4 June 2020
A characteristic class defined for complex vector bundles. A Chern class of the complex vector bundle $ \xi $
over a base $ B $
is denoted by $ c _ {i} ( \xi ) \in H ^ {2i} ( B) $
and is defined for all natural indices $ i $.
By the complete Chern class is meant the inhomogeneous characteristic class $ 1 + c _ {1} + c _ {2} + \dots $,
and the Chern polynomial is the expression $ c _ {t} = 1 + c _ {1} t + c _ {2} t ^ {2} + \dots $,
where $ t $
is a formal unknown. Chern classes were introduced in [1].
The characteristic classes, defined for all $ n $- dimensional complex vector bundles and with values in the integral cohomology, are naturally identified with the elements of the ring $ H ^ {**} ( \mathop{\rm BU} _ {n} ) $. In this sense the Chern classes $ c _ {i} $ can be thought of as elements of the groups $ H ^ {2i} ( \mathop{\rm BU} _ {n} ) $, the complete Chern class as an element of the ring $ H ^ {**} ( \mathop{\rm BU} _ {n} ) $, and the Chern polynomial as an element of the formal power series ring $ H ^ {**} ( \mathop{\rm BU} _ {n} ) [ [ t ] ] $.
The Chern classes satisfy the following properties, which uniquely determine them. 1) For two vector bundles $ \xi , \eta $ with a common base $ B $, $ c ( \xi \oplus \eta ) = c ( \xi ) c ( \eta ) $, in other words $ c _ {k} ( \xi \oplus \eta ) = \sum _ {i} c _ {i} ( \xi ) c _ {k-} i ( \eta ) $ where $ c _ {0} = 1 $. 2) For the one-dimensional universal bundle $ \kappa _ {1} $ over $ \mathbf C P ^ \infty $ the identity $ c ( \kappa _ {1} ) = 1 + u $ holds, where $ u \in H ^ {2} ( \mathbf C P ^ \infty ) $ is the orientation of $ \kappa _ {1} $( $ \mathbf C P ^ \infty $ is the Thom space of $ \kappa _ {1} $, which, being complex, has a uniquely-defined orientation $ u $).
Consequences of the properties 1)–2) are: $ c _ {i} ( \xi ) = 0 $ for $ i > \mathop{\rm dim} \xi $, and $ c ( \xi ) = c ( \xi \oplus \theta ) $, where $ \theta $ is the trivial bundle. The latter fact allows one to define Chern classes as elements of the ring $ H ^ {**} ( \mathop{\rm BU} ) $.
If $ \omega = \{ i _ {1} \dots i _ {k} \} $ is a collection of non-negative integers, then $ c _ \omega $ denotes the characteristic class $ c _ {i _ {1} } \dots c _ {i _ {k} } \in H ^ {2n} ( \mathop{\rm BU} ) $, where $ n = i _ {1} + \dots + i _ {k} $.
Under the natural monomorphism $ H ^ {**} ( \mathop{\rm BU} _ {n} ) \rightarrow H ^ {**} ( \mathop{\rm BT} _ {n} ) = \mathbf Z [ [ x _ {1} \dots x _ {n} ] ] $ induced by the mapping $ \mathop{\rm BT} _ {n} = \mathbf C P ^ \infty \times \dots \times \mathbf C P ^ \infty \rightarrow \mathop{\rm BU} _ {n} $, the Chern classes are mapped into the elementary symmetric functions, and the complete Chern class is mapped to the polynomial $ \prod _ {i=} 1 ^ {n} ( 1 + x _ {i} ) $. The image of the ring $ H ^ {**} ( \mathop{\rm BU} _ {n} ) $ in $ H ^ {**} ( \mathop{\rm BT} _ {n} ) = \mathbf Z [ [ x _ {1} \dots x _ {n} ] ] $ is the subring consisting of all symmetric formal power series. Every symmetric formal power series in the Wu generators $ x _ {1} \dots x _ {n} $ determines a characteristic class that can be expressed in terms of Chern classes. For example, the series $ \prod _ {i=} 1 ^ {n} x _ {i} / ( 1 - e ^ {x _ {i} } ) $ determines a characteristic class with rational coefficients, called the Todd class and denoted by $ T \in H ^ {**} ( \mathop{\rm BU} _ {n} ; \mathbf Q ) $.
Let $ \omega = \{ i _ {1} \dots i _ {k} \} $ be a set of non-negative integers. Let $ S _ \omega ( c _ {1} \dots c _ {n} ) $ denote the characteristic class defined by the smallest symmetric polynomial in the variables $ x _ {1} \dots x _ {n} $, where $ n \geq i _ {1} + \dots + i _ {k} $, containing the monomial $ x _ {1} ^ {i _ {1} } \dots x _ {k} ^ {i _ {k} } $.
Let $ h ^ {*} $ be an oriented multiplicative cohomology theory. Then the Chern classes $ \sigma _ {i} $ with values in $ h ^ {*} $ satisfy, as do ordinary Chern classes, the properties: $ \sigma ( \xi \oplus \eta ) = \sigma ( \xi ) \sigma ( \eta ) $, $ \sigma = 1 + \sigma _ {1} + \sigma _ {2} + \dots $, $ \sigma ( \kappa _ {1} ) = 1 + u \in h ^ {*} ( \mathbf C P ^ \infty ) $, where $ u \in h ^ {2} ( \mathbf C P ^ \infty ) $ is the orientation of the bundle $ \kappa _ {1} $, and these properties completely determine them. As with ordinary Chern classes, one uses the notation $ \sigma _ \omega = \sigma _ {i _ {1} } \dots \sigma _ {i _ {k} } $ and $ S _ \omega ( \sigma _ {1} \dots \sigma _ {n} ) $. If $ \xi , \eta $ are two complex vector bundles, then
$$ S _ \omega ( \sigma _ {1} \dots \sigma _ {n} ) ( \xi \oplus \eta ) = $$
$$ = \ \sum _ {\omega ^ \prime \cup \omega ^ {\prime\prime} = \omega } S _ { \omega ^ \prime } ( \sigma _ {1} \dots \sigma _ {n} ) ( \xi ) S _ {\omega ^ {\prime\prime} } ( \sigma _ {1} \dots \sigma _ {n} ) ( \eta ) , $$
where the summation is taken over all sets $ \omega ^ \prime , \omega ^ {\prime\prime} $ with $ \omega ^ \prime \cup \omega ^ {\prime\prime} = \omega $.
In place of the theory $ h ^ {*} $ one may take a unitary cobordism theory $ U ^ {*} $ or $ K $- theory. For a $ U ^ {*} $- theory the element $ u \in U ^ {2} ( \mathbf C P ^ \infty ) $ is defined by the identity mapping $ \mathbf C P ^ \infty \rightarrow \mathbf C P ^ \infty = \mathop{\rm MU} _ {1} $, and for $ K $- theory $ u = \beta ( 1 - [ \overline{x}\; ] ) \in \widetilde{K} {} ^ {2} ( \mathbf C P ^ \infty ) $, where $ \widetilde \beta : K ^ {0} \rightarrow K ^ {2} $ is the Bott periodicity operator. The notation $ \sigma _ {i} $ is retained for Chern classes with values in a $ U ^ {*} $- theory, while Chern classes with values in $ K $- theory are denoted by $ \gamma _ {i} $.
According to the general theory, $ \gamma _ {i} ( \xi ) \in K ^ {2i} ( B) $, where $ \xi $ is a vector bundle with base $ B $. However $ K $- theory is often conveniently thought of as a $ \mathbf Z _ {2} $- graded theory, identifying the groups $ K ^ {n} ( B) $ and $ K ^ {n+} 2 ( B) $ via the periodicity operator $ \beta $. Then $ K ^ {*} ( B) = K ^ {0} ( B) \oplus K ^ {1} ( B) $ and $ \gamma ( \xi ) \in K ^ {0} ( B) $ for all $ i $. From this point of view it makes sense to consider, instead of the complete Chern class, the Chern polynomial
$$ \gamma _ {t} ( \xi ) = 1 + \sum _ {i > 0 } \gamma _ {i} ( \xi ) t ^ {i} \in K ^ {0} ( B) [ t] . $$
Let $ \lambda ^ {i} ( \xi ) = [ \xi \wedge \dots \wedge \xi ] $ be a cohomology operation in $ K $- theory ( $ i $ terms). The polynomial
$$ \lambda _ {t} ( \xi ) = \sum _ { i= } 0 ^ \infty \lambda ^ {i} ( \xi ) t ^ {i} \in K ^ {0} ( B) [ t] $$
satisfies, as does $ \gamma _ {t} $, the multiplicative property
$$ \lambda _ {t} ( \xi \oplus \eta ) = \ \lambda _ {t} ( \xi ) \lambda _ {t} ( \eta ) . $$
There is the following connection between these polynomials:
$$ \frac{\lambda _ {t} }{1-} t ( \overline \xi \; - \mathop{\rm dim} \xi ) = 1 + \sum _ { i= } 1 ^ \infty (- 1) \gamma _ {i} ( \xi ) t ^ {i} = \ \gamma _ {-} t ( \xi ) . $$
Here both parts of the equation lie in $ K ^ {0} ( B) [ t] $ and $ \xi $ is the trivial bundle of dimension $ \mathop{\rm dim} \xi $. The classes $ \gamma _ {i} $ in this construction are different from those constructed by M.F. Atiyah, who defined them by the formula $ \gamma _ {t} ( \xi ) = ( \lambda _ {t} / ( 1 - t ) ) ( \xi ) $. R. Stong [2] defined classes $ \gamma _ {i} $ that satisfy the condition
$$ \gamma _ {t} ( \xi ) = \frac{\lambda _ {t} }{1-} t ( \overline \xi \; - \mathop{\rm dim} \xi ) . $$
The difference arises because, for Stong,
$$ u = \beta ( [ \kappa _ {1} ] - 1 ) \in \ \widetilde{K} {} ^ {2} ( \mathbf C P ^ \infty ) . $$
The classes $ \sigma _ {i} $ are connected with the notion of a Landweber–Novikov algebra, which is very fruitful in homotopy theory. For an arbitrary set $ \omega = \{ i _ {1} \dots i _ {k} \} $ of non-negative integers, consider the characteristic class $ S _ \omega ( \sigma _ {1} \dots \sigma _ {n} ) \in U ^ {2d} ( \mathop{\rm BU} ) $, where $ d = i _ {1} + \dots + i _ {k} $. There is a Thom isomorphism $ U ^ {2d} ( \mathop{\rm BU} ) \rightarrow \widetilde{U} {} ^ {2d} ( \mathop{\rm MU} ) \subset U ^ {2d} ( \mathop{\rm MU} ) $, where $ \mathop{\rm MU} $ is the spectrum corresponding to the $ U ^ {*} $- theory. The image of the class $ S _ \omega ( \sigma _ {1} \dots \sigma _ {n} ) $ in $ U ^ {2d} ( \mathop{\rm MU} ) $ determines a cohomology operation in the $ U ^ {*} $- theory. The subalgebra of the Steenrod algebra in the $ U ^ {*} $- theory generated by the operations of this form is called the Landweber–Novikov algebra. The operation constructed from the set $ \omega = \{ i _ {1} \dots i _ {k} \} $ is denoted by $ S _ \omega $.
For one-dimensional bundles $ \xi , \eta $ there is the identity
$$ c _ {1} ( \xi \otimes \eta ) = c _ {1} ( \xi ) + c _ {1} ( \eta ) . $$
This important property, which enables one to define the Chern character, does not hold in generalized cohomology theories. However there exists a formal power series $ g ( t) $ with coefficients in $ h ^ {*} ( \mathop{\rm pt} ) \otimes \mathbf Q $, such that $ g ( \sigma _ {1} ( \xi \otimes \eta )) = g ( \sigma _ {1} ( \xi ) ) + g ( \sigma _ {1} ( \eta ) ) $, where $ \sigma _ {1} $ is the first Chern class with coefficients in $ h ^ {*} $. For the unitary cobordism theory
$$ g ( t) = \sum _ { n= } 0 ^ \infty \frac{[ \mathbf C P ^ {n} ] }{n+} 1 t ^ {n+} 1 , $$
where $ [ \mathbf C P ^ {n} ] = \Omega _ {u} ^ {*} = U ^ {*} ( \mathop{\rm pt} ) $ is the cobordism class of the projective space $ \mathbf C P ^ {n} $. This series is called the Mishchenko series.
References
| [1] | S.S. Chern, "Characteristic classes of Hermitian manifolds" Ann. of Math. , 47 : 1 (1946) pp. 85–121 MR0015793 Zbl 0060.41416 |
| [2] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) MR0248858 Zbl 0181.26604 |
| [3] | R.S. Palais, "Seminar on the Atiyah–Singer index theorem" , Princeton Univ. Press (1965) MR0198494 Zbl 0137.17002 |
| [4] | P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) MR0176478 Zbl 0125.40103 |
| [5a] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators I" Ann. of Math. (2) , 87 (1968) pp. 484–530 MR0236950 MR0232402 Zbl 0164.24001 |
| [5b] | M.F. Atiyah, G.B. Segal, "The index of elliptic operators II" Ann. of Math. (2) , 87 (1968) pp. 531–545 MR0236953 MR0236951 Zbl 0164.24201 |
| [5c] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators III" Ann. of Math. (2) , 87 (1968) pp. 546–604 MR0236952 Zbl 0164.24301 |
| [5d] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators IV" Ann. of Math. (2) , 93 (1971) pp. 119–138 MR0279833 Zbl 0212.28603 |
| [5e] | M.F. Atiyah, I.M. Singer, "The index of elliptic operators V" Ann. of Math. (2) , 93 (1971) pp. 139–149 MR0279834 Zbl 0212.28603 |
| [6] | F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) MR1335917 MR0202713 Zbl 0376.14001 |
| [7] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) MR0229247 Zbl 0144.44804 |
| [8] | V.M. Bukhshtaber, "The Chern–Dold character in cobordisms" Math. USSR-Sb. , 12 : 4 (1970) pp. 573–594 Mat. Sb. , 83 (1970) pp. 575–595 Zbl 0219.57027 |
| [9] | S.P. Novikov, "The method of algebraic topology from the viewpoint of cobordism theory" Math. USSR-Izv. , 4 : 1 (1967) pp. 827–913 Izv. Akad. SSSR Ser. Mat. , 31 : 4 (1967) pp. 855–951 |
| [10] | M.F. Atiyah, "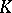 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
Comments
$ H ^ {**} ( X) $ denotes the completion $ \prod _ {i \geq 0 } H ^ {i} ( X) $ of $ H ^ {*} ( X) = \oplus _ {i \geq 0 } H ^ {i} ( X) $.
The power series $ g ( t) \in h ^ {*} ( \mathop{\rm pt} ) \otimes \mathbf Q $ for a complex oriented cohomology theory $ h ^ {*} $ such that $ g ( \sigma _ {1} ( \xi \otimes \eta ) ) = g ( \sigma _ {1} ( \xi ) ) + g ( \sigma _ {1} ( \eta ) ) $ is the logarithm of the formal group $ F _ {h} ( X , Y ) $ defined by $ h ^ {*} $; cf. Cobordism and Formal group for some more details.
Chern class. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Chern_class&oldid=46333