Formal group
An algebraic analogue of the concept of a local Lie group (cf. Lie group, local). The theory of formal groups has numerous applications in algebraic geometry, class field theory and cobordism theory.
A formal group over a field $ k $ is a group object in the category of connected affine formal schemes over $ k $ ( see [1], [4], [6], [7]). Let $ H _{A} $ be the functor that associates with an algebra $ B $ the set of algebra homomorphism $ A \rightarrow B $ from some Noetherian commutative local $ k $ - algebra $ A $ with maximal ideal $ m $ and field of residues $ k $ , complete in the $ m $ - adic topology, such that the homomorphisms map $ m $ into the set $ \mathop{\rm nil}\nolimits (B) $ of nilpotent elements of $ B $ . Then a connected affine formal scheme is a covariant functor $ H $ from the category of finite-dimensional commutative $ k $ - algebras $ B $ into the category of sets that is isomorphic to an $ H _{A} $ . That $ H $ is a group object means that there is a group structure given on all the sets $ H (B) $ such that for every $ k $ - algebra homomorphism $ B _{1} \rightarrow B _{2} $ the corresponding mapping $ H (B _{1} ) \rightarrow H (B _{2} ) $ is a group homomorphism. If all the groups $ H (B) $ are commutative, then the formal group $ H $ is said to be commutative. Every connected group scheme $ G $ over $ k $ defines a formal group $ G: \ B \rightarrow G (B) $ . Here one can take as $ A $ the completion of the local ring of $ G $ at the unit element.
If $ A $ is the ring $ k [[X _{1} \dots X _{2} ]] $ of formal power series in $ n $ variables over $ k $ , then $ H $ is called an $ n $ - dimensional formal Lie group. For a connected algebraic group $ G $ over $ k $ , $ \widehat{G} $ is a formal Lie group. A formal Lie group $ H $ is isomorphic, as a functor in the category of sets, to the functor $ D ^{n} : \ B \rightarrow \mathop{\rm nil}\nolimits (B) ^{n} $ that associates with an algebra $ B $ the $ n $ - fold Cartesian product of its nil radical $ \mathop{\rm nil}\nolimits (B) $ with itself. The group structure on the sets $ H (B) = \mathop{\rm nil}\nolimits (B) ^{n} $ is given by a formal group law — a collection of $ n $ formal power series in $ 2n $ variables $ X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} $ : $$ F _{1} (X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} ) \dots $$ $$ F _{n} (X _{1} \dots X _{n} ,\ Y _{1} \dots Y _{n} ), $$ satisfying the following conditions:$$ F _{i} (X,\ 0) = X _{i} , F _{i} (0,\ Y) = Y _{i} , $$ $$ F _{i} (X _{1} \dots X _{n} ,\ F _{1} (Y,\ Z) \dots F _{n} (Y,\ Z)) = $$ $$ = F _{i} (F _{1} (X,\ Y) \dots F _{n} (X,\ Y),\ Z _{1} \dots Z _{n} ) . $$ Here $ X = (X _{1} \dots X _{n} ) $ , $ Y = (Y _{1} \dots Y _{n} ), $ $ Z = (Z _{1} \dots Z _{n} ) $ , $ 0 = (0 \dots 0) $ . This group law on the sets $ H (B) = \mathop{\rm nil}\nolimits (B) ^{n} $ is given by the formulas$$ (x _{1} \dots x _{n} ) \circ (y _{1} \dots y _{n} ) = (z _{1} \dots z _{n} ), $$ where $ z _{i} = F _{i} (x _{1} \dots x _{n} ,\ y _{1} \dots y _{n} ) $ ; because $ x $ and $ y $ are nilpotent, all except a finite number of terms of the series are zero. Every formal group law gives group structures on $ \mathop{\rm nil}\nolimits (B) ^{n} $ by means of
and converts the functor $ D ^{n} $ into a formal Lie group. The concept of a formal group law, and thus of a formal Lie group, can be generalized to the case of arbitrary commutative ground rings (see [2], [5]). Sometimes by a formal group one means just a formal Lie group or even a formal group law.
Just as for local Lie groups (cf. Lie group, local) one can define the Lie algebra of a formal Lie group. Over fields $ k $ of characteristic 0 the correspondence between a formal Lie group and its Lie algebra defines an equivalence of the respective categories. In characteristic $ p > 0 $ the situation is more complicated. Thus, over an algebraically closed field (for $ p > 0 $ ) there is a countable number of pairwise non-isomorphic one-dimensional commutative formal Lie groups [1], while all one-dimensional Lie algebras are isomorphic [3]. Over perfect fields of finite characteristic, commutative formal Lie groups are classified by means of Dieudonné modules (see [1], [6]).
The theory of formal groups over fields can be generalized to the case of arbitrary formal ground schemes [7].
References
| [1] | Yu.I. Manin, "The theory of commutative formal groups over fields of finite characteristic" Russian Math. Surveys , 18 (1963) pp. 1–80 Uspekhi Mat. Nauk , 18 : 6 (1963) pp. 3–90 MR157972 Zbl 0128.15603 |
| [2] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) MR0248858 Zbl 0181.26604 |
| [3] | J.-P. Serre, "Lie algebras and Lie groups" , Benjamin (1965) (Translated from French) MR0218496 Zbl 0132.27803 |
| [4] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
| [5] | M. Lazard, "Commutative formal groups" , Springer (1975) MR0393050 Zbl 0304.14027 |
| [6] | J.-M. Fontaine, "Groupes f04082068.png-divisibles sur les corps locaux" Astérique , 47–48 (1977) MR498610 |
| [7] | B. Mazur, J.T. Tate, "Canonical height pairings via biextensions" J.T. Tate (ed.) M. Artin (ed.) , Arithmetic and geometry , 1 , Birkhäuser (1983) pp. 195–237 MR0717595 Zbl 0574.14036 |
Comments
A universal formal group law (for $ n $ - dimensional formal group laws) is an $ n $ - dimensional formal group law $ F _{u} ( X ,\ Y) \in L [ X ,\ Y ] $ , $ X = ( X _{1} \dots X _{n} ) $ , $ Y = ( Y _{1} \dots Y _{n} ) $ such that for every $ n $ - dimensional formal group law $ F ( X ,\ Y ) $ over a ring $ A $ there is a unique homomorphism of rings $ \phi _{F} : \ L \rightarrow A $ such that $ \phi _{F} ^{*} F _{u} ( X ,\ Y ) = F ( X ,\ Y ) $ . Here $ \phi _{F} ^{*} F _{u} ( X ,\ Y ) $ denotes the result of applying $ \phi _{F} ^{*} $ to the coefficients of the $ n $ power series $ F _{u} ( X ,\ Y ) $ . Universal formal group laws exist and are unique in the sense that if $ F _{u} ^ {\ \prime} ( X ,\ Y ) $ over $ L ^ \prime $ is another one, then there exists a ring isomorphism $ \psi : \ L \rightarrow L ^ \prime $ such that $ \psi ^{*} F _{u} ( X ,\ Y ) = F _{u} ^ {\ \prime} ( X ,\ Y ) $ .
For commutative formal group laws explicit formulas are available for the construction of universal formal group laws, cf. [a3]. The underlying ring $ L $
is a ring of polynomials in infinitely many indeterminates (Lazard's theorem).
A homomorphism of formal group laws $ \alpha : \ F ( X ,\ Y ) \rightarrow G ( X ,\ Y ) $ , $ \mathop{\rm dim}\nolimits \ F = n $ , $ \mathop{\rm dim}\nolimits \ G = m $ , is an $ m $ - tuple of power series in $ n $ - variables $ \alpha ( Z _{1} \dots Z _{n} ) $ , $ \alpha _{i} (0) = 0 $ , such that $ \alpha ( F ( X ,\ Y ) ) = G ( \alpha (X) ,\ \alpha (Y)) $ . The homomorphism is an isomorphism if there exists an inverse homomorphism $ \beta $ such that $ \alpha ( \beta (X) ) = X $ , and it is a strict isomorphism of formal group laws if $ \alpha _{i} (Z) = Z _{i} + $ ( higher order terms).
Let $ A $ be a ring of characteristic zero, i.e. the homomorphism of rings $ \mathbf Z \rightarrow A $ which sends $ 1 \in \mathbf Z $ to the unit element in $ A $ is injective. Then $ A \rightarrow A \otimes _ {\mathbf Z} \mathbf Q $ is injective. Over $ A \otimes _ {\mathbf Z} \mathbf Q $ all commutative formal group laws are strictly isomorphic and hence isomorphic to the additive formal group law$$ G _{a} ( X ,\ Y ) = ( X _{1} + Y _{1} \dots X _{n} + Y _{n} ) . $$ It follows that for every commutative formal group law $ F ( X ,\ Y ) $ over $ A $ there exists a unique $ n $ - tuple of power series $ f (X) $ , $ f _{i} (X) = X _{i} + \dots $ with coefficients in $ A \otimes _ {\mathbf Z} \mathbf Q $ such that$$ F ( X ,\ Y ) = f ^ {\ -1} ( f (X) + f (Y) ) , $$ where $ f ^ {\ -1} (z) $ is the "inverse function" to $ f (Z) $ , i.e. $ f ^ {\ -1} ( f (Z) ) = Z $ . This $ f (X) $ is called the logarithm of the group law $ F ( X ,\ Y ) $ .
The formal group law of complex cobordism is a universal one-dimensional formal group law (Quillen's theorem) and its logarithm is given by Mishchenko's formula$$
\mathop{\rm log}\nolimits \ F _ {\mathbf M \mathbf U} (X) =
\sum _{i=1} ^ \infty
i ^{-1} [ \mathbf C \mathbf P ^{i-1} ]
X ^{i} .
$$
Combined with the explicit construction of a one-dimensional universal group law these facts yield useful information on the generators of the complex cobordism ring $ \mathbf M \mathbf U ^{*} ( \mathop{\rm pt}\nolimits ) $ .
Cf. Cobordism for more details.
Let $ F ( X ,\ Y ) $ be an $ n $ - dimensional group law over $ A $ . A curve over $ A $ in $ F $ is an $ n $ - tuple of power series $ \gamma (T) $ in one variable such that $ \gamma (0) = 0 $ . Two curves can be added by $ \gamma (T) + _{F} \delta (T) = F ( \gamma (T) ,\ \delta (T) ) $ . The set of curves is given the natural power series topology and there results a commutative topological group $ {\mathbf C} ( F ; \ A ) $ . The group $ {\mathbf C} ( F ; \ A ) $ admits a number of operators $ V _{n} $ , $ F _{n} $ , $ [a] $ , $ a \in A $ , defined as follows:$$ V _{n} \gamma (T) = \gamma ( T ^{n} ) , $$ $$ [a] \gamma (T) = \gamma ( a T ) , $$ $$ F _{n} \gamma (T) = \gamma ( \zeta _{n} T ^{1}/n ) + _{F} \dots + _{F} \gamma ( \zeta _{n} ^{n} T ^{1}/n ) = {\sum _ i=1 ^ n} {} ^{F} \gamma ( \zeta _{n} ^{i} T ^{1}/n ) , $$ where $ \zeta _{n} $ is a primitive $ n $ - th root of unity. There are a number of relations between these operators and they combine to define a (non-commutative) ring $ \mathop{\rm Cart}\nolimits (A) $ , which generalizes the Dieudonné ring, cf. Witt vector for the latter. Cartier's second and third theorems on formal group laws say that the $ \mathop{\rm Cart}\nolimits (A) $ modules $ {\mathbf C} ( F ; \ A ) $ classify formal groups and they characterize which groups occur as $ {\mathbf C} ( F ; \ A ) $ ' s. This is the covariant classification of commutative formal groups in contrast with the earlier contravariant classification of commutative formal groups over perfect fields by Dieudonné modules.
Let $ W : \ \mathbf{Rinj} \rightarrow \mathbf{Rinj} $ be the functor of Witt vectors (cf. Witt vector). Let $ G _{m} ( X ,\ Y ) = X + Y + X Y $ be the (one-dimensional) multiplicative formal group law over $ A $ . Then $ W (A) = {\mathbf C} ( G _{m} ; A ) $ . Cartier's first theorem for formal group laws says that the functor $ F \mapsto {\mathbf C} ( F ; \ A ) $ is representable. More precisely, let $ \widehat{W} $ be the (infinite-dimensional) formal group law given by the addition formulas of the Witt vectors and let $ \gamma _{0} (T) $ be the curve $ (T ,\ 0 ,\ 0 ,\dots ) $ . Then for every formal group law $ F ( X ,\ Y ) $ and curve $ \gamma (T) \in {\mathbf C} ( F ; \ A ) $ there is unique homomorphism of formal group laws $ \alpha _ \gamma : \ \widehat{W} \rightarrow F $ such that $ \alpha _ \gamma ( \gamma _{0} (T) ) = \gamma (T) $ .
There exists a Pontryagin-type duality between commutative formal groups and commutative affine (algebraic) groups over a field $ k $ ,
called Cartier duality. Cf. [a3], [a4] for more details. Correspondingly, Dieudonné modules are also important in the classification of commutative affine (algebraic) groups. Essentially, Cartier duality comes from the "duality" between algebras and co-algebras; cf. Co-algebra.
Let $ A $ be a discrete valuation ring with finite residue field $ k $ and maximal ideal $ \mathfrak m = ( \pi ) $ . The Lubin–Tate formal group law associated to $ ( A ,\ \pi ) $ is defined by the logarithm$$ f _ \pi (X) = X + \pi ^{-1} X ^{q} + \pi ^{-2} X ^ {q ^{2}} + \dots . $$ Then $ F _ \pi ( X ,\ Y ) = f _ \pi ^ {\ -1} ( f _ \pi (X) + f _ \pi (Y) ) $ has its coefficients in $ A $ . These formal group laws are in a sense formal $ p $ - adic analogues of elliptic curves with complex multiplication in that they have maximally large endomorphism rings. They are also analogues in the role they play vis à vis the class field theory of $ K $ , the quotient field of $ A $ . Indeed, let $ F _ \pi ( \bar{\mathfrak m} ) $ be the set $ \bar{\mathfrak m} $ with the addition $ a + b = F _ \pi ( a ,\ b ) $ . Here $ \bar{\mathfrak m} $ is the maximal ideal of the ring of integers of an algebraic closure of $ K $ . Then a maximal Abelian totally ramified extension of $ K $ is generated by the torsion elements of $ F ( \bar{\mathfrak m} ) $ ; cf. [a3], [a5] for more details.
Formal groups also are an important tool in algebraic geometry, especially in the theory of Abelian varieties. This holds even more so for a generalization: $ p $ - divisible groups; cf. $ p $ - divisible group.
Lazard's theorem on one-dimensional formal group laws says that all one-dimensional formal group laws over a ring without nilpotents are commutative.
Let $ F ( X ,\ Y ) $ be a one-dimensional formal group law. Define inductively $ [n] (X) = F ( X ,\ [ n - 1 ] (X) ) $ , $ n \geq 2 $ , $ [1] (X) = X $ . Let $ F $ be defined over a field $ k $ of characteristic $ p > 0 $ . Then $ [p] (X) $ is necessarily of the form $ X ^ {p ^{h}} + $ ( higher degree terms) or is equal to zero. The positive integer $ h $ is called the height of $ F $ ; if $ [p] (X) = 0 $ , the height of $ F $ is taken to be $ \infty $ . Over an algebraically closed field of characteristic $ p > 0 $ the one-dimensional formal group laws are classified by their heights, and all heights $ 1 ,\ 2 \dots \infty $ occur.
Let $ F ( X ,\ Y ) $ be a one-dimensional formal group law over a ring $ A $ in which every prime number except $ p $ is invertible, e.g. $ A $ is the ring of integers of a local field of residue characteristic $ p $ or $ A $ is a field of characteristic $ p $ . Assume for the moment that $ A $ is of characteristic zero and let$$ f (X) = X + a _{2} X ^{2} + a _{3} X ^{3} + \dots $$ be the logarithm of $ F ( X ,\ Y ) $ . Then $ F ( X ,\ Y ) $ is strictly isomorphic over $ A $ to the formal group law $ F _{(p)} ( X ,\ Y ) $ whose logarithm is equal to$$ f _{(p)} (X) = X + a _{p} X ^{p} + a _ {p ^{2}} X ^ {p ^{2}} + \dots . $$ The result extends to the case that $ A $ is not of characteristic zero and to more-dimensional commutative formal group laws. $ F _{(p)} ( X ,\ Y) $ is called the $ p $ - typification of $ F ( X ,\ Y ) $ .
References
| [a1] | J.T. Tate, "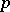 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 -divisible groups" T.A. Springer (ed.) et al. (ed.) , Proc. Conf. local fields (Driebergen, 1966) , Springer (1967) pp. 158–183 MR0231827 Zbl 0157.27601 |
| [a2] | J.-P. Serre, "Groupes 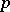 -divisible (d' après J. Tate)" Sem. Bourbaki , 19, Exp. 318 (1966–1967) MR1610452 MR0393040 -divisible (d' après J. Tate)" Sem. Bourbaki , 19, Exp. 318 (1966–1967) MR1610452 MR0393040 |
| [a3] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) MR0506881 MR0463184 Zbl 0454.14020 |
| [a4] | M. Demazure, P. Gabriel, "Groupes algébriques" , 1 , Masson & North-Holland (1970) MR0302656 MR0284446 Zbl 0223.14009 Zbl 0203.23401 |
| [a5] | J. Lubin, J. Tate, "Formal complex multiplication in local fields" Ann. of Math. , 81 (1965) pp. 380–387 MR0172878 Zbl 0128.26501 |
Formal group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Formal_group&oldid=44249