Topological structures

Introduction.

General topology (also called set-theoretic topology or analytic topology, cf. Topology, general) tries to explain such concepts as convergence and continuity known from classical analysis in a general setting. Originally, this was done for metric spaces (M. Fréchet [a10], 1906), and later on for the topological spaces (F. Hausdorff [a11], 1914) which are known today as Hausdorff spaces. The usual concept of a topological space goes back to C. Kuratowski [a25] (1922), who axiomatized the idea of "closure" and thus explained "nearness" between a point $ x $ and a set $ A $( usually denoted by $ x \in \overline{A}\; $, i.e. $ x $ belongs to the closure of $ A $). But the ideas of uniform continuity; uniform convergence; and completeness (in topology), which make sense for metric spaces, could not be explained for topological spaces. Therefore, uniform spaces were introduced (A. Weil [a33] (1937) defined them by means of "entourages" and J.W. Tukey [a32] (1940) by means of "uniform covers" , cf. also Uniform space). For the same reason V.A. Efremovich [a7] (1952) studied "proximity spaces" by axiomatizing the concept of "nearness between two sets" (cf. also Proximity space). Hereafter several attempts were made to combine topological and uniform concepts, e.g. L. Nachbin (1949) studied quasi-uniform spaces (cf. [a9]), A. Császár (1957) invented syntopogeneous spaces (cf. [a5]), D.B. Doitchinov [a6] (1964) introduced generalized topological spaces (or supertopological spaces), M. Katětov [a21] (1965) studied merotopic spaces (or semi-nearness spaces) and H. Herrlich [a13] (1974) invented nearness spaces. The intuitive concept of "nearness" which is fundamental in topology has now found a satisfactory definition: namely, by means of nearness spaces (respectively, merotopic spaces) "nearness of an arbitrary collection of sets" is explicable.

Since continuity of mappings between topological spaces cannot be explained by means of convergent sequences, as in classical analysis, more general concepts were needed. Therefore, E.H. Moore and H.L. Smith [a26] (1922) developed the theory of nets (cf. Net (of sets in a topological space)) and later on H. Cartan [a3] (1937) introduced filters (cf. Filter). Because of the existence of ultrafilters (cf. Ultrafilter) the theory of filters is preferably used in general topology. By axiomatizing the concept of filter convergence one obtains limit spaces — a generalization of topological spaces. They were first investigated by H.-J. Kowalsky [a24] (1954) and, independently, by H.R. Fischer [a8] (1959). With respect to the study of function spaces, limit spaces are more convenient than topological spaces. A more restrictive notion, namely the notion of pseudo-topological space ( $ = $ Choquet space), was studied before by G. Choquet [a4] (1948). Many other concepts have been developed, e.g. convergence spaces by D.C. Kent [a23] (1964) and filter-merotopic spaces (i.e. grill-determined semi-nearness spaces) by Katětov [a21] (1965).

All the above-mentioned types of spaces are structured sets. The structure-preserving mappings between them are called continuous or uniformly continuous, respectively. Thus, many concrete categories are obtained. The striking similarities of constructions in these categories led to the definition of topological categories and the investigation of their relationships to each other. So, a new discipline, called categorical topology, was created (about 1971) (cf. Herrlich [a12] (1971) and O. Wyler [a34] (1971)).

The terminology of this article corresponds to [a19] and [a28].

Topological categories.

By a concrete category one means a category $ {\mathcal C} $ whose objects are structured sets, i.e. pairs $ ( X, \xi ) $ where $ X $ is a set and $ \xi $ is a $ {\mathcal C} $- structure on $ X $, whose morphisms $ f: ( X, \xi ) \rightarrow ( Y, \mu ) $ are suitable mappings between $ X $ and $ Y $, and whose composition is the usual composition of mappings — in other words: a category $ {\mathcal C} $ together with a faithful (i.e. forgetful) functor $ {\mathcal U} : {\mathcal C} \rightarrow \mathop{\rm Set} $ from $ {\mathcal C} $ into the category $ \mathop{\rm Set} $ of sets (and mappings).

A concrete category $ {\mathcal C} $ is called topological if and only if it satisfies the following conditions:

$ \mathop{\rm Cat} \mathop{\rm top} _ {1} $). Existence of initial structures. For any set $ X $, any family $ (( X _ {i} , \xi _ {i} )) _ {i \in I } $ of $ {\mathcal C} $- objects indexed by some class $ I $ and any family $ ( f _ {i} : X \rightarrow X _ {i} ) _ {i \in I } $ of mappings indexed by $ I $, there exists a unique $ {\mathcal C} $- structure $ \xi $ on $ X $ which is initial with respect to $ ( X, f _ {i} , ( X _ {i} , \xi _ {i} ), I) $, i.e. such that for any $ {\mathcal C} $- object $ ( Y, \mu ) $ a mapping $ g: ( Y, \mu ) \rightarrow ( X, \xi ) $ is a $ {\mathcal C} $- morphism if and only if for every $ i \in I $ the composite mapping $ ( f _ {i} \circ g): ( Y, \mu ) \rightarrow ( X _ {i} , \xi _ {i} ) $ is a $ {\mathcal C} $- morphism.

$ \mathop{\rm Cat} \mathop{\rm top} _ {2} $). Fibre-smallness. For any set $ X $, the $ {\mathcal C} $- fibre of $ X $, i.e. the class of all $ {\mathcal C} $- structures on $ X $, is a set.

$ \mathop{\rm Cat} \mathop{\rm top} _ {3} $). Terminal separator property. For any set $ X $ of cardinality one there exists precisely one $ {\mathcal C} $- structure on $ X $.

Examples of topological categories.

1) The category $ \mathop{\rm Top} $ of topological spaces (and continuous mappings).

2) The category $ \mathop{\rm Unif} $ of uniform spaces (and uniformly-continuous mappings).

3) The category $ \mathop{\rm Prox} $ of proximity spaces (and $ \delta $- mappings).

4) The categories $ \mathop{\rm Conv} $, $ \mathop{\rm Lim} $ and $ \mathop{\rm PsTop} $ of convergence spaces, limit spaces and pseudo-topological spaces (and continuous mappings), respectively.

(Let $ X $ be a set, $ F ( X) $ the set of all filters on $ X $ and $ q $ a subset of $ F ( X) \times X $ such that the following conditions are satisfied:

$ \mathop{\rm Lim} _ {1} $) $ ( \dot{x} , x) \in q $ for each $ x \in X $, where $ \dot{x} $ denotes the set of all subsets $ A $ of $ X $ containing $ x $; and

$ \mathop{\rm Lim} _ {2} $) $ ( {\mathcal G} , x) \in q $ whenever $ ( {\mathcal F} , x) \in q $ and $ {\mathcal F} \subset {\mathcal G} $.

Then $ ( X, q) $ is called a convergence space if: (C) $ ( {\mathcal F} , x) \in q $ implies $ ( {\mathcal F} \cap \dot{x} , x) \in q $; a limit space if: $ \mathop{\rm Lim} _ {3} $) $ ( {\mathcal F} , x) \in q $ and $ ( {\mathcal G} , x) \in q $ imply $ ( {\mathcal F} \cap {\mathcal G} , x) \in q $; and a pseudo-topological space or Choquet space if $ \mathop{\rm PsT} $) $ ( {\mathcal F} , x) \in q $ whenever $ ( {\mathcal G} , x) \in q $ for each ultrafilter $ {\mathcal G} \supset {\mathcal F} $.

Instead of $ ( {\mathcal F} , x) \in q $ one usually writes $ {\mathcal F} \rightarrow x $( read: $ {\mathcal F} $ converges to $ x $). In each case the morphisms are all continuous mappings, i.e. those carrying filters converging to $ x $ to filters converging to $ f ( x) $.)

5) The category $ \mathop{\rm SynTop} $ of syntopogeneous spaces (and continuous mappings) (cf. [a5]).

6) The category $ \mathop{\rm SuperTop} $ of supertopological spaces (and continuous mappings) (cf. [a6]).

7) The category $ \mathop{\rm QuasiUnif} $ of quasi-uniform spaces (and quasi-uniformly continuous mappings) (cf. [a9]).

8) The categories $ \mathop{\rm Mer} $ of merotopic spaces (and uniformly-continuous mappings) and $ \mathop{\rm Near} $ of nearness spaces (and uniformly-continuous mappings).

(Let $ X $ be a set and let $ \mu $ be a non-empty set of non-empty coverings of $ X $ such that the following conditions are satisfied:

$ N _ {1} $) if $ {\mathcal A} $ refines $ {\mathcal B} $ and $ {\mathcal A} \in \mu $, then $ {\mathcal B} \in \mu $;

$ N _ {2} $) if $ {\mathcal A} \in \mu $ and $ {\mathcal B} \in \mu $, then $ \{ {A \cap B } : {A \in {\mathcal A} \textrm{ and } B \in {\mathcal B} } \} \in \mu $.

Then $ ( X, \mu ) $ is called a merotopic space, or semi-nearness space, and the elements of $ \mu $ are called uniform coverings.

A merotopic space $ ( X, \mu ) $ is called a nearness space if the following condition is satisfied:

$ N _ {3} $) If $ {\mathcal A} \in \mu $, then $ \{ { { \mathop{\rm int} } _ \mu A } : {A \in {\mathcal A} } \} \in \mu $, where $ { \mathop{\rm int} } _ \mu A = \{ {x \in X } : {A, X \setminus \{ x \} \in \mu } \} $. If $ ( X, \mu ) $ and $ ( Y, \mu ) $ are merotopic spaces (respectively, nearness spaces), then a mapping $ f: X \rightarrow Y $ is called uniformly continuous if and only if $ f ^ { - 1 } {\mathcal A} = \{ {f ^ { - 1 } [ A] } : {A \in {\mathcal A} } \} \in \mu $ for each $ {\mathcal A} \in \eta $.)

9) The category $ \mathop{\rm BiTop} $ of bitopological spaces (and pairwise continuous mappings) (cf. [a22]).

10) The category $ \mathop{\rm Born} $ of bornological spaces (and bounded mappings) (cf. [a20]).

11) The category $ \mathop{\rm Simp} $ of simplicial complexes (and simplicial mappings) (cf. [a30]).

12) The categories $ \mathop{\rm Rere} $ of reflexive relations and $ \mathop{\rm PrOrd} $ of pre-ordered sets (the objects of $ \mathop{\rm Rere} $( respectively, $ \mathop{\rm PrOrd} $) are pairs $ ( X, \rho ) $ where $ X $ is a set and $ \rho $ is a reflexive (respectively, reflexive and transitive) relation on $ X $; in each case, morphisms are relation-preserving mappings).

13) The category $ \mathop{\rm CGTop} $ of compactly-generated topological spaces (and continuous mappings) (i.e. the smallest coreflective subcategory of $ \mathop{\rm Top} $ containing the category $ \mathop{\rm CompT} _ {2} $ of compact Hausdorff spaces (and continuous mappings)).

14) The categories $ \mathop{\rm Conv} _ {s} $, $ \mathop{\rm Lim} _ {s} $, $ \mathop{\rm PsTop} _ {s} $, and $ \mathop{\rm Top} _ {s} $ of symmetric convergence spaces, symmetric limit spaces, symmetric pseudo-topological spaces, and symmetric topological spaces (and continuous mappings).

(A convergence space $ ( X, q) $ is called symmetric if

$$ ( S) \ \ ( {\mathcal F} , y) \in q \ \textrm{ and } \ x \in \cap {\mathcal F} \ \textrm{ imply } \ ( {\mathcal F} , x) \in q. $$

In particular, a topological space $ X $ is symmetric if and only if it is an $ R _ {0} $- space, i.e. $ x \in \overline{ {\{ y \} }}\; $ implies $ y \in \overline{ {\{ x \} }}\; $ for each $ ( x, y) \in X \times X $.)

15) The category $ \mathop{\rm Grill} $ of grill-determined semi-nearness spaces (and uniformly continuous mappings).

(A semi-nearness space $ ( X, \mu ) $ is called grill-determined if every near collection $ {\mathcal A} $ of subsets of $ X $ is contained in some near grill $ {\mathcal G} $ on $ X $. Here, a collection $ {\mathcal B} $ of subsets of $ X $ is called near if for each $ {\mathcal C} \in \mu $ there is some $ C \in {\mathcal C} $ such that $ C \cap B \neq \phi $ for each $ B \in {\mathcal B} $, and a grill if $ \phi \notin {\mathcal B} $ and for each pair $ ( A, B) $ of subsets of $ X $ one has $ A \cup B \in {\mathcal B} $ if and only if $ A \in {\mathcal B} $ or $ B \in {\mathcal B} $.

The category $ \mathop{\rm Grill} $ is isomorphic to the category $ \mathop{\rm Fil} $, defined as follows: the objects of $ \mathop{\rm Fil} $ are pairs $ ( X, \gamma ) $ where $ X $ is a set and $ \gamma $ is a set of filters on $ X $ such that the following conditions hold: 1) if $ {\mathcal F} \in \gamma $, and a filter $ {\mathcal G} $ is finer than $ {\mathcal F} $, then $ {\mathcal G} \in \gamma $; and 2) for every $ x \in X $, $ \dot{x} \in \gamma $. The morphisms $ f: ( X, \gamma ) \rightarrow ( X ^ \prime , \gamma ^ \prime ) $ are the mappings $ f: X \rightarrow X ^ \prime $ such that for each $ {\mathcal F} \in \gamma $ the filter generated by $ \{ {f [ F] } : {F \in {\mathcal F} } \} $ belongs to $ \gamma ^ \prime $.)

16) The category $ \mathop{\rm Cont} $ of contigual nearness spaces (and uniformly-continuous mappings).

(A nearness space $ ( X, \mu ) $ is called contigual if for each $ A \in \mu $ there exists a finite $ {\mathcal B} \subset {\mathcal A} $ with $ {\mathcal B} \in \mu $.)

17) The category $ \mathop{\rm SubTop} $ of subtopological nearness spaces (and uniformly-continuous mappings).

(A nearness space $ ( X, \mu ) $ is called subtopological if it can be imbedded in a topological nearness space (i.e. symmetric topological space). Note that the category $ \mathop{\rm Top} _ {s} $ is isomorphic to the category $ \mathop{\rm T}\AAh Near $ of topological nearness spaces (and uniformly-continuous mappings). Here a nearness space $ ( X, \mu ) $ is called topological if $ X = \cup \{ { { \mathop{\rm int} } _ \mu A } : {A \in {\mathcal A} } \} $ implies $ {\mathcal A} \in \mu $.)

Properties of topological categories.

1) The condition $ \mathop{\rm Cat} \mathop{\rm top} _ {1} $) may be replaced by the following equivalent one (existence of final structures): For any set $ X $, any family $ (( X _ {i} , \xi _ {i} )) _ {i \in I } $ of $ {\mathcal C} $- objects indexed by some class $ I $ and any family $ ( f _ {i} : X _ {i} \rightarrow X) _ {i \in I } $ of mappings indexed by $ I $, there exists a unique $ {\mathcal C} $- structure $ \xi $ on $ X $ which is final with respect to $ (( X _ {i} , \xi _ {i} ), f _ {i} , X, I) $, i.e. for any $ {\mathcal C} $- object $ ( Y, \mu ) $ a mapping $ g: ( X, \xi ) \rightarrow ( Y, \mu ) $ is a $ {\mathcal C} $- morphism if and only if for every $ i \in I $ the composite mapping $ g \circ f _ {i} : ( X _ {i} , \xi _ {i} ) \rightarrow ( Y, \mu ) $ is a $ {\mathcal C} $- morphism.

2) Let $ {\mathcal C} $ be a topological category. Then the following hold:

$ {\mathcal C} $ is complete and co-complete, and the forgetful functor $ U: {\mathcal C} \rightarrow \mathop{\rm Set} $ lifts limits via initiality and co-limits via finality from $ \mathop{\rm Set} $ to $ {\mathcal C} $.

A $ {\mathcal C} $- morphism is a monomorphism (epimorphism; bimorphism) if and only if it is injective (surjective, bijective).

$ {\mathcal C} $ is wellpowered and co-wellpowered.

For any $ {\mathcal C} $- morphism $ f: ( X, \xi ) \rightarrow ( Y, \mu ) $ the following conditions are equivalent: a) $ f $ is an imbedding of categories, i.e. $ f $ is injective and $ \xi $ is initial with respect to $ ( Y, \mu ) $ and $ f $; b) $ f $ is an extremal monomorphism; and c) $ f $ is a regular monomorphism.

For any $ {\mathcal C} $- morphism $ f: ( X, \xi ) \rightarrow ( Y, \mu ) $ the following conditions are equivalent: a) $ f $ is a quotient mapping, i.e. $ f $ is surjective and $ \eta $ is final with respect to $ ( X, \xi ) $ and $ f $; b) $ f $ is an extremal epimorphism; and c) $ f $ is a regular epimorphism.

$ {\mathcal C} $ is an (epi, embedding)-category and a (quotient, mono)-category.

The forgetful functor $ U: {\mathcal C} \rightarrow \mathop{\rm Set} $ has a full and faithful left adjoint, i.e. for any set $ X $ there exists a discrete structure $ \xi _ {X} $ on $ X $, distinguished by the property that any mapping $ f: ( X, \xi _ {X} ) \rightarrow ( Y, \eta ) $ is a $ {\mathcal C} $- morphism.

The forgetful functor $ U: {\mathcal C} \rightarrow \mathop{\rm Set} $ has a full and faithful right adjoint, i.e. for any set $ X $ there exists a non-discrete $ {\mathcal C} $- structure $ \xi ^ {X} $ on $ X $ distinguished by the property that any mapping $ f: ( Y, \eta ) \rightarrow ( X, \xi ^ {X} ) $ is a $ {\mathcal C} $- morphism.

For any set $ X $, the $ {\mathcal C} $- fibre of $ X $, ordered by $ \xi \leq \mu $ $ \iff $ $ 1 _ {X} : ( X, \xi ) \rightarrow ( X, \eta ) $ is a $ {\mathcal C} $- morphism, is a complete lattice.

For any set $ X \neq \emptyset $, any constant mapping $ f: ( X, \xi ) \rightarrow ( Y, \eta ) $ is a $ {\mathcal C} $- morphism.

Any $ {\mathcal C} $- object $ ( X, \xi ) $ with $ X \neq \emptyset $ is a separator.

A $ {\mathcal C} $- object $ C $ is a co-separator if and only if there exists an imbedding of a non-discrete object with two points into $ C $.

A $ {\mathcal C} $- object $ ( X, \xi ) $ is projective if and only if $ \xi $ is the discrete structure on $ X $( cf. also Projective object of a category).

A $ {\mathcal C} $- object $ ( X, \xi ) $ is injective if and only if $ X \neq \emptyset $ and $ \xi $ is the non-discrete structure on $ X $( cf. also Injective object).

3) In order to describe the relationships between topological categories, the theory of reflections and co-reflections is extremely useful. Below, subcategories are always assumed to be full and isomorphism closed. (A subcategory $ {\mathcal A} $ of a category $ {\mathcal C} $ is called isomorphism closed if each $ {\mathcal C} $- object isomorphic to some $ {\mathcal A} $- object is an $ {\mathcal A} $- object; for being full see Full subcategory.) If $ {\mathcal A} $ is a subcategory of a category $ {\mathcal C} $ and $ {\mathcal J} : {\mathcal A} \rightarrow {\mathcal C} $ denotes the inclusion functor, then $ {\mathcal A} $ is called reflective (respectively, co-reflective) in $ {\mathcal C} $ if one of the two following (equivalent) conditions is satisfied: a) $ {\mathcal J} $ has a left adjoint $ {\mathcal R} $( respectively, right adjoint $ {\mathcal R} _ {C} $) called a reflector (respectively, a co-reflector); or b) for each $ {\mathcal C} $- object $ X $ there exist an $ {\mathcal A} $- object $ X _ {\mathcal A} $ and a $ {\mathcal C} $- morphism $ r _ {X} : X \rightarrow X _ {\mathcal A} $, called an $ {\mathcal A} $- reflection of $ X $( respectively, $ m _ {X} : X _ {\mathcal A} \rightarrow X $, called an $ {\mathcal A} $- coreflection of $ X $), such that for each $ {\mathcal A} $- object $ Y $ and each $ {\mathcal C} $- morphism $ f: X \rightarrow Y $( respectively, $ f: Y \rightarrow X $) there is a unique $ {\mathcal A} $- morphism ( $ = {\mathcal C} $- morphism) $ \overline{f}\; : X _ {\mathcal A} \rightarrow Y $( respectively, $ \overline{f}\; : Y \rightarrow X _ {\mathcal A} $) such that $ \overline{f}\; \circ r _ {X} = f $( respectively, $ m _ {X} \circ \overline{f}\; = f $).

Further, a subcategory $ {\mathcal A} $ is called epireflective (monocoreflective), extremal epireflective (extremal monocoreflective) or bireflective (bicoreflective) in $ {\mathcal C} $, respectively, if $ {\mathcal A} $ is reflective (coreflective) and for each $ {\mathcal C} $- object $ X $, the $ {\mathcal A} $- reflections ( $ {\mathcal A} $- coreflections) of $ X $ are epimorphisms (monomorphisms), extremal epimorphisms (extremal monomorphisms) or bimorphisms, respectively.

For topological categories the following two assertions hold:

Any bireflective (and any bicoreflective) subcategory of a topological category is a topological category.

Let $ {\mathcal A} $ be a subcategory of a topological category $ {\mathcal C} $. Then the following hold:

a) $ {\mathcal A} $ is epireflective (extremal epireflective) in $ {\mathcal C} $ if and only if $ {\mathcal A} $ is closed under formation of products and subobjects (i.e. extremal monomorphisms) (weak subobjects, i.e. monomorphisms) in $ {\mathcal C} $;

b) $ {\mathcal A} $ is bireflective in $ {\mathcal C} $ if and only if $ {\mathcal A} $ is reflective in $ {\mathcal C} $ and contains all non-discrete objects of $ {\mathcal C} $;

c) if $ {\mathcal A} $ contains at least one object with non-empty underlying set, then the following conditions are equivalent:

( $ \alpha $) $ {\mathcal A} $ is coreflective in $ {\mathcal C} $;

( $ \beta $) $ {\mathcal A} $ is bicoreflective in $ {\mathcal C} $;

( $ \gamma $) $ {\mathcal A} $ is closed under formation of coproducts and quotient objects in $ {\mathcal C} $;

( $ \delta $) $ {\mathcal A} $ is coreflective in $ {\mathcal C} $ and contains all discrete objects of $ {\mathcal C} $.

The relations between several topological categories are illustrated in the diagram below hold. Here $ R $( respectively, $ C $) stands for imbedding as a bireflective (respectively, bicoreflective) subcategory.

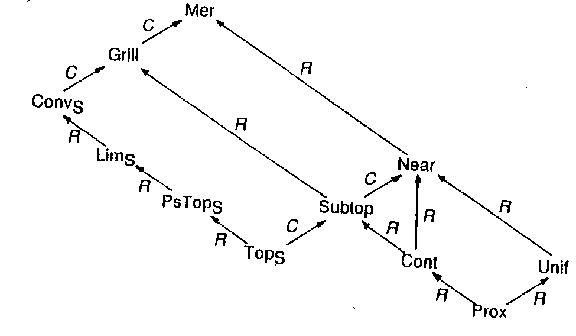
Figure: t093150a

Concerning the formation of initial and final structures in the topological categories listed in the diagram, one may use the following result: If $ {\mathcal A} $ is a bireflective (respectively, bicoreflective) subcategory of some topological category $ {\mathcal C} $, then the initial structures (respectively, final structures) in $ {\mathcal A} $ are formed as in $ {\mathcal C} $, whereas the final structures (respectively, initial structures) are formed in $ {\mathcal C} $ by applying the left adjoint $ {\mathcal R} $( respectively, right adjoint $ {\mathcal R} _ {C} $) of the inclusion functor $ {\mathcal I} : {\mathcal A} \rightarrow {\mathcal C} $( i.e. the final structures (respectively, initial structures) in $ {\mathcal A} $ are obtained from the final structures (respectively, initial structures) in $ {\mathcal C} $ by bireflective (respectively, bicoreflective) modification).

Example.

The symmetric topological spaces (or topological nearness spaces) form a bicoreflective subcategory of $ \mathop{\rm Near} $: If $ ( X, \mu ) $ is a topological nearness space, then the identity mapping $ 1 _ {X} : ( X, \mu _ {t} ) \rightarrow ( X, \mu ) $ is a $ \mathop{\rm T}\AAh Near $- coreflection, where $ \mu _ {t} $ consists of all coverings $ {\mathcal A} $ of $ X $ such that $ X = \cup \{ { { \mathop{\rm int} } _ \mu A } : {A \in {\mathcal A} } \} $; the corresponding coreflector $ T: \mathop{\rm Near} \rightarrow \mathop{\rm T}\AAh Near $ assigns to each nearness space $ ( X, \mu ) $ the topological nearness space $ ( X, \mu _ {t} ) $, i.e. its bicoreflective modification.

First, consider the construction of subspaces and products in $ \mathop{\rm Near} $.

Subspaces.

Let $ ( X, \mu ) $ be a nearness space, $ A $ a subset of $ X $ and $ i: A \rightarrow X $ the inclusion mapping. Then there is a unique initial $ \mathop{\rm Near} $- structure $ \mu _ {A} $ on $ A $ with respect to $ i $ and $ ( X, \mu ) $, namely $ \mu _ {A} = \{ \{ A \} \wedge {\mathcal U} : {\mathcal U} \in \mu \} $ where $ \{ A \} \wedge {\mathcal U} = \{ {A \cap U } : {U \in {\mathcal U} } \} $. The pair $ ( A, \mu _ {A} ) $ is called a nearness subspace of $ ( X, \mu ) $.

Products.

Let $ (( X _ {i} , \mu _ {i} )) _ {i \in I } $ be a family of nearness spaces indexed by some set $ I $, let $ \prod X _ {i} $ be the Cartesian product of the family $ ( X _ {i} ) _ {i \in I } $( cf. Direct product) and let $ p _ {i} : \prod X _ {i} \rightarrow X _ {i} $ be the projection mapping for each $ i \in I $. Then there is a unique initial $ \mathop{\rm Near} $- structure $ \mu $ on $ \prod X _ {i} $ with respect to $ ( \prod X _ {i} , p _ {i} , ( X _ {i} , \mu _ {i} ), I) $, namely the set $ \mu $ of all coverings of $ \prod X _ {i} $ which are refined by some finite intersection of elements of $ \{ {p _ {i} ^ {-} 1 {\mathcal U} _ {i} } : { {\mathcal U} _ {i} \in \mu _ {i } \textrm{ and } i \in I } \} $, where $ p _ {i} ^ {-} 1 {\mathcal U} _ {i} = \{ {p _ {i} ^ {-} 1 [ U _ {i} ] } : {U _ {i} \in {\mathcal U} _ {i} } \} $ and the intersection $ {\mathcal A} \wedge {\mathcal B} $ of two coverings $ {\mathcal A} $ and $ {\mathcal B} $ of some set $ X $ is defined to be the covering $ \{ {A \cap B } : {A \in {\mathcal A} \textrm{ and } B \in {\mathcal B} } \} $. The pair $ ( \prod X _ {i} , \mu ) $ is called the nearness product space of $ (( X _ {i} , \mu _ {i} )) _ {i \in I } $.

Secondly, subspaces and products in $ \mathop{\rm T}\AAh Near $ are constructed by forming them first in $ \mathop{\rm Near} $ and then applying the coreflector $ T $. In this way one obtains the usual constructions of subspaces and products for (symmetric) topological spaces. But it is this second step that destroys desirable statements, e.g. the following:

1) products of paracompact topological spaces are paracompact;

2) products of compact Hausdorff spaces with normal $ R _ {0} $- spaces are normal;

3) subspaces of paracompact topological spaces (normal $ R _ {0} $- spaces) are paracompact (normal);

4) $ \mathop{\rm dim} ( X \times Y) \leq \mathop{\rm dim} X + \mathop{\rm dim} Y $ for paracompact topological spaces;

5) $ \mathop{\rm dim} X = \mathop{\rm dim} Y $ for dense subspaces $ X $ of regular $ R _ {0} $- spaces $ Y $.

Each of the above statements is false when products and subspaces are formed in the usual (topological) sense, but all of them are true when products and subspaces are formed in $ \mathop{\rm Near} $, and then they are special cases of more general theorems. Consider, for example, the situation for paracompact spaces: A nearness space $ ( X, \mu ) $ is called paracompact provided that it is a uniform $ N _ {1} $- space. Here a nearness space $ ( X, \mu ) $ is called an $ N _ {1} $- space if the underlying topological space $ T (( X, \mu )) $ is a $ T _ {1} $- space, and uniform if each $ {\mathcal A} \in \mu $ is star-refined by some $ {\mathcal B} \in \mu $. Thus, uniform nearness spaces are uniform spaces (described by uniform coverings) and uniform $ N _ {1} $- spaces are separated uniform spaces, whereas the paracompact topological spaces are precisely those $ N _ {1} $- spaces which are simultaneously topological and uniform. Then products and subspaces of paracompact nearness spaces are paracompact nearness spaces. In particular, products and subspaces (in $ \mathop{\rm Near} $) of paracompact topological spaces are paracompact, but in general not topological. Further information can be found in, for example, [a14] and [a28].

Generalizations.

Initially structured (i.e. monotopological) categories. Epireflective (respectively, extremal epireflective) subcategories of topological categories are not topological, in general. E.g. the category $ \mathop{\rm Haus} $ of Hausdorff spaces (and continuous mappings) is an extremal epireflective subcategory of $ \mathop{\rm Top} $, but $ \mathop{\rm Haus} $ is not topological (note that the imbedding of the Hausdorff space $ \mathbf Q $ of rational numbers into the Hausdorff space $ \mathbf R $ of real number is an epimorphism in $ \mathop{\rm Haus} $ which is not surjective). In order to include $ \mathop{\rm Haus} $ in the present consideration, one needs the following definition: A concrete category $ {\mathcal C} $ is called initially structured (or monotopological) if it satisfies $ \mathop{\rm Cat} \mathop{\rm top} _ {2} $) and $ \mathop{\rm Cat} \mathop{\rm top} _ {3} $) and if for any set $ X $, any family $ (( X _ {i} , \xi _ {i} )) _ {i \in I } $ of $ {\mathcal C} $- objects indexed by some class $ I $ and any mono-source $ ( f _ {i} : X \rightarrow X _ {i} ) _ {i \in I } $ of mappings indexed by $ I $( i.e. any family $ ( f _ {i} : X \rightarrow X _ {i} ) _ {i \in I } $ of mappings such that for any pair $ Y _ {\rightarrow _ \beta } ^ {\rightarrow ^ \alpha } X $ of mappings with $ f _ {i} \circ \alpha = f _ {i} \circ \beta $ for each $ i \in I $, it follows that $ \alpha = \beta $) there exists a unique $ {\mathcal C} $- structure $ \xi $ on $ X $ which is initial with respect to $ ( X, f _ {i} , ( X _ {i} , \xi _ {i} ), I) $.

Obviously, every topological category is initially structured. Furthermore, every epireflective (respectively, extremal epireflective) subcategory of a topological category (respectively, initially structured category) is initially structured. E.g. the categories $ \mathop{\rm Top} _ {0} $( topological $ T _ {0} $- spaces), $ \mathop{\rm Top} _ {1} $( topological $ T _ {1} $- spaces), $ \mathop{\rm Reg} _ {1} $( regular topological $ T _ {1} $- spaces) $ \mathop{\rm CompReg} _ {1} $( completely-regular topological $ T _ {1} $- spaces), $ \mathop{\rm Poset} $( partially ordered sets), $ \mathop{\rm HConv} $( Hausdorff convergence spaces), $ \mathop{\rm HLim} $( Hausdorff limit spaces), and $ \mathop{\rm HPsTop} $( Hausdorff pseudo-topological spaces) (the Hausdorff property in the last three examples means that limits of filters are unique) are initially structured categories which are not topological. Conversely, every initially structured category is an extremal epireflective subcategory of some topological category. Initially structured categories are complete, cocomplete and wellpowered, but they do not have all the nice properties of topological categories; in particular, they are not cowellpowered (e.g. the category of $ T _ {2a} $- spaces (i.e. Urysohn spaces, cf. Urysohn space) (and continuous mappings) is initially structured, but not cowellpowered). See [a28] for further details.

Topological categories over arbitrary base categories. First some definitions. Let $ {\mathcal F} : {\mathcal C} \rightarrow {\mathcal X} $ be a functor. A pair $ ( A, ( f _ {i} : A \rightarrow A _ {i} ) _ {i \in I } ) $ where $ A $ is a $ {\mathcal C} $- object and $ ( f _ {i} : A \rightarrow A _ {i} ) _ {i \in I } $ a class-indexed family of $ {\mathcal C} $- morphisms each with domain $ A $, called a source in $ {\mathcal C} $, is $ {\mathcal F} $- initial if and only if for each source $ ( B, ( g _ {i} : B \rightarrow A _ {i} ) _ {i \in I } ) $ in $ {\mathcal C} $ and each $ {\mathcal X} $- morphism $ f: {\mathcal F} ( B) \rightarrow {\mathcal F} ( A) $ such that $ {\mathcal F} ( f _ {i} ) \circ f = {\mathcal F} ( g _ {i} ) $ for each $ i \in I $, there exists a unique $ {\mathcal C} $- morphism $ \overline{f}\; : B \rightarrow A $ with $ {\mathcal F} ( \overline{f}\; ) = f $ and $ f _ {i} \circ \overline{f}\; = g _ {i} $ for each $ i \in I $. A functor $ {\mathcal F} : {\mathcal C} \rightarrow X $ is called topological if for each class-indexed family $ ( A _ {i} ) _ {i \in I } $ of $ {\mathcal C} $- objects and each source $ ( X, ( f _ {i} : X \rightarrow {\mathcal F} ( A _ {i} )) _ {i \in I } ) $ in $ {\mathcal X} $ there exists a unique $ {\mathcal F} $- initial source $ ( A, ( g _ {i} : A \rightarrow A _ {i} ) _ {i \in I } ) $ in $ {\mathcal C} $ with $ {\mathcal F} ( A) = X $ and $ {\mathcal F} ( g _ {i} ) = f _ {i} $ for each $ i \in I $. Let $ {\mathcal X} $ be a fixed category, called base category. A concrete category over $ {\mathcal X} $ is pair $ ( {\mathcal C} , {\mathcal F} ) $ where $ {\mathcal C} $ is a category and $ {\mathcal F} : {\mathcal C} \rightarrow {\mathcal X} $ a functor which is faithful, amnestic (i.e. any $ {\mathcal C} $- isomorphism $ f $ is a $ {\mathcal C} $- identity if and only if $ {\mathcal F} ( f) $ is an $ {\mathcal X} $- identity) and transportable (i.e. for each $ {\mathcal C} $- object $ A $, each $ {\mathcal X} $- object $ B $ and each isomorphism $ q: B \rightarrow {\mathcal F} ( A) $ there exists a unique $ {\mathcal C} $- object $ C $ and an isomorphism $ \overline{q}\; : C \rightarrow A $ with $ {\mathcal F} ( \overline{q}\; ) = q $). The functor $ {\mathcal F} $ is called the underlying functor of $ ( {\mathcal C} , {\mathcal F} ) $. Occasionally, $ ( {\mathcal C} , {\mathcal F} ) $ is denoted by $ C $. A concrete category $ ( {\mathcal C} , {\mathcal F} ) $ over $ {\mathcal F} $ is called initially complete if $ {\mathcal F} : {\mathcal C} \rightarrow {\mathcal X} $ is topological, it is called small-fibred if for each $ {\mathcal X} $- object $ X $ the class of all $ {\mathcal C} $- objects $ A $ with $ {\mathcal F} ( A) = X $ is a set, and it is called topological if it is initially complete and small-fibred.

Obviously, if $ {\mathcal C} $ is a topological category as defined at the beginning of this article and if $ {\mathcal F} : {\mathcal C} \rightarrow \mathop{\rm Set} $ denotes the forgetful functor, then $ ( {\mathcal C} , {\mathcal F} ) $ is topological over $ \mathop{\rm Set} $. But the axiom $ \mathop{\rm Cat} \mathop{\rm top} _ {3} $), which is equivalent to the fact that all constant mappings (i.e. functions that factor through $ \{ \emptyset \} $) between $ {\mathcal C} $- objects are $ {\mathcal C} $- morphisms, is now omitted. Thus, e.g., the category $ \mathop{\rm Graph} $ of directed graphs and (graph homomorphisms) is no longer excluded. Base categories other than $ \mathop{\rm Set} $ are, e.g.,

1) the category $ {\mathcal T} $ with $ \{ \emptyset \} $ as single object and the identity mapping as single morphism. Then concrete categories over $ {\mathcal T} $ are partially ordered classes. Topological categories over $ {\mathcal T} $ are complete lattices.

2) The category $ \mathop{\rm Group} $ of groups (and homomorphisms). Then the category $ \mathop{\rm TopGroup} $ of topological groups (and continuous homomorphisms) is topological over $ \mathop{\rm Group} $.

3) The category $ {\mathcal C} $ whose objects are pairs $ ( A, B) $ of disjoint sets and whose morphisms $ F: ( A, B) \rightarrow ( A ^ \prime , B ^ \prime ) $ are mappings $ F: A \cup B \rightarrow A ^ \prime \cup B ^ \prime $ such that $ F [ A] \subset A ^ \prime $ and $ F [ B] \subset B ^ \prime $. Then the category $ \mathop{\rm Net} $ whose objects are triples $ ( A, B, R) $, where $ ( A, B) $ is a $ {\mathcal C} $- object and $ R \subset ( A \times B) \cup ( B \times A) $, and whose morphisms $ F: ( A, B, R) \rightarrow ( A ^ \prime , B ^ \prime , R ^ \prime ) $ are $ {\mathcal C} $- morphisms $ F: ( A, B) \rightarrow ( A ^ \prime , B ^ \prime ) $ such that $ ( F ( x), F ( y)) \in R ^ \prime $ for each $ ( x, y) \in R $, is topological over $ {\mathcal C} $( note that the objects of $ \mathop{\rm Net} $ are called nets; nets are used in computer science, cf. [a29]).

Topological functors are faithful, amnestic and transportable. Thus, they lead to concrete categories which are initially complete. If $ {\mathcal C} $ is a topological category over $ {\mathcal X} $ with underlying functor $ {\mathcal F} $, then according to the results on topological categories over $ \mathop{\rm Set} $, one obtains: $ {\mathcal F} $ has a full and faithful left adjoint and a full and faithful right adjoint, $ {\mathcal F} $ lifts limits via initiality and colimits via finality from $ {\mathcal X} $ to $ {\mathcal C} $, any factorization structure on $ {\mathcal X} $ can be lifted via initiality (respectively, via finality) to a factorization structure on $ {\mathcal C} $, completeness, cocompleteness, wellpoweredness and cowellpoweredness hold in $ {\mathcal C} $ if and only if they hold in $ {\mathcal X} $, fibres are complete lattices, etc. Moreover, duality holds, i.e. if $ {\mathcal C} $ is topological over $ {\mathcal X} $, then the dual category (cf. Category) $ {\mathcal C} ^ {op} $ of $ {\mathcal C} $ is topological over $ {\mathcal X} ^ {op} $.

Cartesian closedness and further restrictions.

The category $ \mathop{\rm Top} $ of topological spaces and continuous mappings fails to have some desirable properties, e.g. the product of two quotient mappings need not be a quotient mapping and there is in general no natural function space topology, i.e. $ \mathop{\rm Top} $ is not Cartesian closed (cf. Category). Because of this fact, which is inconvenient for investigations in algebraic topology (homotopy theory), functional analysis (duality theory) or topological algebra (quotients), $ \mathop{\rm Top} $ has been substituted either by well-behaved subcategories or by more convenient supercategories. The precise ideas are as follows.

1) A category $ {\mathcal C} $ is Cartesian closed if the following conditions are satisfied (cf. also Category):

a) for each pair $ ( A, B) $ of $ {\mathcal C} $- objects, there exists a product $ A \times B $ in $ {\mathcal C} $;

b) for each $ {\mathcal C} $- object $ A $ holds: For each $ {\mathcal C} $- object $ B $, there exist some $ {\mathcal C} $- object $ B ^ {A} $ and some $ {\mathcal C} $- morphism $ e _ {A, B } : A \times B ^ {A} \rightarrow B $ such that for each $ {\mathcal C} $- object $ C $ and each $ {\mathcal C} $- morphism $ f: A \times C \rightarrow B $ there exists a unique $ {\mathcal C} $- morphism $ \overline{f}\; : C \rightarrow B ^ {A} $ such that the diagram

$$ \begin{array}{lcr} A \times B ^ {A} &\rightarrow ^ { {e _ {A,} B } } & B \\ size - 3 {1 _ {A} \times \overline{f}\; } &{} &size - 3 {f } \\ {} &A \times C &{} \\ \end{array} $$

commutes (i.e. for each $ {\mathcal C} $- object $ A $ the functor $ A \times - : {\mathcal C} \rightarrow {\mathcal C} $, defined by $ ( A \times -) ( B) = A \times B $ for each $ {\mathcal C} $- object $ B $ and $ ( A \times -) ( f) = 1 _ {A} \times f $ for each $ {\mathcal C} $- morphism $ f $, has a right adjoint, denoted by $ \bullet ^ {A} $); the objects of the form $ B ^ {A} $ are called power objects.

2) Let $ {\mathcal C} $ be a category. A class-indexed family $ ( f _ {i} : B _ {i} \rightarrow B) _ {i \in I } $ of $ {\mathcal C} $- morphisms is called an epi-sink if for any pair $ ( \alpha , \beta ) $ of $ {\mathcal C} $- morphisms with domain $ B $ such that $ \alpha \circ f _ {i} = \beta \circ f _ {i} $ for each $ i \in I $, it follows that $ \alpha = \beta $.

3) Let $ {\mathcal C} $ be a topological category. An epi-sink $ ( f _ {i} : B _ {i} \rightarrow B) _ {i \in I } $ is called final if the $ {\mathcal C} $- structure of $ B $ is final with respect to $ ( f _ {i} ) _ {i \in I } $.

For a topological category $ {\mathcal C} $ the following assertions are equivalent:

$ {\mathcal C} $ is Cartesian closed;

For any $ {\mathcal C} $- object $ A $ and any set-indexed family $ ( B _ {i} ) _ {i \in I } $ of $ {\mathcal C} $- objects the following are satisfied:

a) $ A \times \amalg _ {i \in I } B _ {i} \cong \amalg _ {i \in I } ( A \times B _ {i} ) $( more exactly: $ A \times \amalg $ preserves coproducts), and

b) If $ f $ is a quotient mapping then so is $ 1 _ {A} \times f $, i.e. $ A \times - $ preserves quotient mappings;

a) For any $ {\mathcal C} $- object $ A $ and any set-indexed family $ ( B _ {i} ) _ {i \in I } $ of $ {\mathcal C} $- objects one has:

$ A \times \amalg _ {i \in I } B _ {i} \cong \amalg _ {i \in I } ( A \times B _ {i} ) $( more exactly: $ A \times - $ preserves coproducts), and

b) In $ {\mathcal C} $ the product $ f \times g $ of any two quotient mappings $ f $ and $ g $ is a quotient mapping;

For each $ {\mathcal C} $- object $ A $ the functor $ A \times - $ preserves final epi-sinks: for any final epi-sink $ ( f _ {i} : B _ {i} \rightarrow B) _ {i \in I } $ in $ {\mathcal C} $, $ ( 1 _ {A} \times f _ {i} : A \times B _ {i} \rightarrow A \times B) _ {i \in I } $ is a final epi-sink;

For each pair $ ( A, B) \in | {\mathcal C} | \times | {\mathcal C} | $, the set $ [ A, B] _ {\mathcal C} $ of all $ {\mathcal C} $- morphisms from $ A $ to $ B $ can be endowed with the structure of a $ {\mathcal C} $- object, denoted by $ B ^ {A} $, such that

a) the evaluation mapping $ e _ {A,B} : A \times B ^ {A} \rightarrow B $, defined by $ e _ {A,B} ( a, g) = g ( a) $ for each $ ( a, g) \in A \times B ^ {A} $, is a $ {\mathcal C} $- morphism;

b) for each $ {\mathcal C} $- object $ C $, the mapping $ \psi : ( B ^ {A} ) ^ {C} \rightarrow B ^ {A \times C } $ defined by $ \psi ( f) = e _ {A,B} \circ ( 1 _ {A} \times f ) $ for each $ {\mathcal C} $- morphism $ f: C \rightarrow B ^ {A} $, is surjective.

4) It follows that for a Cartesian closed topological category $ {\mathcal C} $ the following holds:

$ \alpha $) the first exponential law: $ A ^ {B \times C } \cong ( A ^ {B} ) ^ {C} $;

$ \beta $) the second exponential law: $ ( \prod _ {i \in I } A _ {i} ) ^ {B} \cong \prod _ {i \in I } A _ {i} ^ {B} $;

$ \gamma $) the third exponential law: $ A ^ {\amalg _ {i \in I } B _ {i} } \cong \prod _ {i \in i } A ^ {B _ {i} } $;

$ \delta $) the distributive law: $ A \times \amalg _ {i \in i } B _ {i} \cong \amalg _ {i \in I } A \times B _ {i} $.

Examples of Cartesian closed topological categories are: $ \mathop{\rm Set} $, $ \mathop{\rm PsTop} $, $ \mathop{\rm Lim} $, $ \mathop{\rm Conv} $, $ \mathop{\rm Grill} $, $ \mathop{\rm Born} $, $ \mathop{\rm Simp} $, $ \mathop{\rm Rere} $, $ \mathop{\rm PrOrd} $, $ \mathop{\rm CGTop} $.

5) If $ {\mathcal C} $ is an initially structured category, then $ {\mathcal C} $ is Cartesian closed if and only if for each $ {\mathcal C} $- object $ A $ the functor $ A \times - $ preserves final epi-sinks. Furthermore, in a Cartesian closed initially structured category $ {\mathcal C} $ the power object $ B ^ {A} $ may be interpreted (up to isomorphism) as the set $ [ A, B] _ {\mathcal C} $ endowed with a suitable $ {\mathcal C} $- structure, i.e. as a "function space" , and the $ {\mathcal C} $- morphism $ e _ {A,B} $ is the usual evaluation mapping (up to isomorphism). Since every extremal epireflective subcategory of a Cartesian closed initially structured category is Cartesian closed, one obtains that the categories $ \mathop{\rm Poset} $, $ \mathop{\rm HConv} $( Hausdorff convergence spaces), $ \mathop{\rm HLim} $( Hausdorff limit spaces), and $ \mathop{\rm HPsTop} $( Hausdorff pseudo-topological spaces), respectively (the Hausdorff property means in each case that limits of filters are unique) are Cartesian closed initially structured categories, because they are extremal epireflective in $ \mathop{\rm PrOrd} $, $ \mathop{\rm Conv} $, $ \mathop{\rm Lim} $, and $ \mathop{\rm PsTop} $, respectively (see, e.g., [a28]). Since some of the Cartesian closed topological categories mentioned above satisfy another nice property too, it is useful to define the following: A category $ {\mathcal C} $ is called a topos (quasi-topos) if the following conditions are satisfied: $ {\mathcal A} $ has finite limits and colimits; $ {\mathcal A} $ is Cartesian closed; and in $ {\mathcal A} $( strong) partial morphisms are representable, i.e. for each $ {\mathcal A} $- object $ A $ there exists a (strong) monomorphism $ m _ {A} : A \rightarrow A ^ {*} $ universal in the following sense: given a (strong) partial morphism into $ A $( i.e. a pair consisting of a (strong) monomorphism $ m: B \rightarrow C $ and a morphism $ f: B \rightarrow A $), there exists a unique pullback

$$ \begin{array}{ccc} B &\rightarrow ^ { f } & A \\ size - 3 {m } \downarrow &{} &\downarrow size - 3 {m _ {A} } \\ C &\rightarrow &A ^ {*} \\ \end{array} $$

Obviously, every topos is a quasi-topos. From the above-mentioned Cartesian closed topological categories only $ \mathop{\rm Set} $ is a topos (note that topoi are balanced categories, i.e. categories in which every bimorphism is an isomorphism). Since in each category that has pushouts strong monomorphisms coincide with extremal monomorphisms, strong monomorphisms may be replaced by imbeddings if $ {\mathcal C} $ is a topological category. For a topological category $ {\mathcal C} $ one thus finds that the following conditions are equivalent:

$ {\mathcal C} $ is a quasi-topos;

$ {\mathcal C} $ is Cartesian closed and every $ {\mathcal C} $- object $ A $ can be imbedded via the addition of a single point $ \infty _ {A} $ into a $ {\mathcal C} $- object $ A ^ {*} = A \cup \{ \infty _ {A} \} $ such that the following holds: For every $ {\mathcal C} $- morphism $ f: C \rightarrow A $ from a subobject $ C $ of $ B $ into $ A $, the unique function $ f ^ { * } : B \rightarrow A ^ {*} $ defined by

$$ f ^ { * } ( b) = \ \left \{ \begin{array}{ll} f ( b) & \textrm{ if } b \in C, \\ \infty _ {A} & \textrm{ if } b \notin C, \\ \end{array} \right .$$

is a $ {\mathcal C} $- morphism;

in $ {\mathcal C} $ final epi-sinks are universal, i.e. if $ ( f _ {i} : A _ {i} \rightarrow A) _ {i \in I } $ is a final epi-sink in $ {\mathcal C} $, $ f: B \rightarrow A $ is a $ {\mathcal C} $- morphism and for each $ i \in I $ the diagram

$$ \begin{array}{ccc} B _ {i} &\rightarrow ^ {h _ i} &A _ {i} \\ size - 3 {g _ {i} } \downarrow &{} &\downarrow size - 3 {f _ {i} } \\ B &\rightarrow _ { f } & A \\ \end{array} $$

is a pullback in $ {\mathcal C} $, then $ ( g _ {i} : B _ {i} \rightarrow B) _ {i \in I } $ is a final epi-sink in $ {\mathcal C} $;

a) $ {\mathcal C} $ is Cartesian closed, and

b) in $ {\mathcal C} $ final (epi-)sinks are hereditary, i.e. if $ ( f _ {i} : A _ {i} \rightarrow A) _ {i \in I } $ is a final (epi-)sink in $ {\mathcal C} $, $ B $ is a subspace of $ A $, $ B _ {i} $ is a subspace of $ A _ {i} $ with underlying set $ f _ {i} ^ { - 1 } [ B] $, and $ g _ {i} : B _ {i} \rightarrow B $ is the corresponding restriction of $ f _ {i} $, then $ ( g _ {i} : B _ {i} \rightarrow B) _ {i \in I } $ is also a final (epi-)sink in $ {\mathcal C} $.

Alternative names for topological categories which are quasi-topoi are strongly topological categories and topological universes.

Examples of quasi-topoi are: $ \mathop{\rm PsTop} $, $ \mathop{\rm Lim} $, $ \mathop{\rm Conv} $, $ \mathop{\rm Grill} $, $ \mathop{\rm Born} $, $ \mathop{\rm Simp} $, $ \mathop{\rm Rere} $.

In particular, topological categories which are quasi-topoi have hereditary quotients (cf.

above), a condition whose usefulness has become apparent in the study of connectedness properties in topological categories (cf. [a18] and [a27]). Even in $ \mathop{\rm Mer} $ final sinks are hereditary, though $ \mathop{\rm Mer} $ is not Cartesian closed. Since Cartesian closedness is a convenient property for topological categories (cf. [a31]), the quasi-topos property may be considered to be an ultra-convenient property (cf. [a35]). Hence it seems desirable to find, for a given topological category $ {\mathcal C} $ and a given convenient (respectively, ultra-convenient) property $ P $, a smallest extension $ P ( {\mathcal C} ) $ of $ {\mathcal C} $ satisfying $ P $. Such an extension is called a $ P $- hull of $ {\mathcal C} $. Considerable efforts have been made to construct such hulls. For further details see e.g. [a16].

Cartesian closed topological categories over arbitrary base categories can even have concrete powers (a topological category $ {\mathcal C} $ over a base category $ {\mathcal X} $ with underlying functor $ {\mathcal F} $ is said to have concrete powers if for all objects $ A $ and $ B $ both $ {\mathcal F} ( B ^ {A} ) = {\mathcal F} ( B) ^ { {\mathcal F} ( A) } $ and the evaluation mappings in $ {\mathcal C} $ and $ {\mathcal X} $ coincide), e.g. $ \mathop{\rm Graph} $ and $ \mathop{\rm Net} $ are quasi-topoi with concrete powers. For investigations on Cartesian closedness of topological categories over arbitrary base categories and quasi-topoi see e.g. [a1] and [a15].

Final remarks.

It has turned out that several desirable properties concerning, e.g., paracompactness, normality or dimension which are false in $ \mathop{\rm Top} $ become true when $ \mathop{\rm Top} $ is replaced by $ \mathop{\rm Near} $, which is nicely imbedded in $ \mathop{\rm Mer} $. Even for the investigation of function spaces the subcategory $ \mathop{\rm Grill} $ of $ \mathop{\rm Mer} $, for example, is better behaved than $ \mathop{\rm Top} $. By means of a suitable completion, called canonical completion (or Herrlich completion), of a nearness space well-known extensions and compactifications such as the Wallman extension, Hewitt's realcompactification, Aleksandrov's one-point compactification and the Stone–Čech compactification are obtained. Even every Hausdorff compactification (respectively, regular Hausdorff extension) of a topological space can be obtained by means of canonical completion (cf. e.g. [a17] and [a28] for further details). Last but not least, the Čech homology and cohomology theory used in algebraic topology has a suitable generalization to nearness spaces (respectively, merotopic spaces), where the fundamental idea is to replace open coverings by uniform coverings (cf., e.g., [a2] and [a28] for more detailed information).

References

[a1]	J. Adámek, H. Herrlich, "Cartesian closed categories, quasitopoi and topological universes" Comm. Math. Univ. Carolinae , 27 (1986) pp. 235–257
[a2]	H.L. Bently, "Homology and cohomology for merotopic and nearness spaces" Quaest. Math. , 6 (1978) pp. 541–568
[a3]	H. Cartan, "Théorie des filtres" Comp. Rend. , 205 (1937) pp. 595–598
[a4]	G. Choquet, "Convergences" Ann. Univ. Grenoble Sect. Sci. Math. Phys. (N.S.) , 23 (1948) pp. 57–112
[a5]	A. Császár, "Foundations of general topology" , Macmillan (1963)
[a6]	D.B. Doitchinov, "A unified theory of topological spaces, proximity spaces and uniform spaces" Soviet Math. Dokl. , 5 (1964) pp. 595–598 Dokl. Akad. Nauk SSSR , 5 (1964)
[a7]	V.A. Efremovič, "Geometry of proximity" Math. USSR Sb. , 31 : 73 (1952) pp. 189–200 Mat. Sb. , 31 : 73 (1952)
[a8]	H.R. Fischer, "Limesräume" Math. Ann. , 137 (1959) pp. 269–303
[a9]	P. Fletscher, W.F. Lindgren, "Quasi-uniform spaces" , M. Dekker (1982)
[a10]	M. Fréchet, "Sur quelques points du calcul fonctionnel" Rend. Palermo , 22 (1906) pp. 1–74
[a11]	F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978))
[a12]	H. Herrlich, "Categorical topology" General Topol. Appl. , 1 (1071) pp. 1–15
[a13]	H. Herrlich, "Topological structures" , Math. Centre Tracts , 52 , Math. Centre , Amsterdam (1974) pp. 59–122
[a14]	H. Herrlich, "Some topological theorems which fail to be true" , Categorical Topology , Lect. notes in math. , 540 , Springer (1976) pp. 265–285
[a15]	H. Herrlich, "Universal topology" , Categorical Topology , Sigma Ser. Pure Math. , Heldermann (1984) pp. 223–281
[a16]	H. Herrlich, "Topological improvements of categories of structured sets" General Topol. Appl. , 27 (1987) pp. 145–155
[a17]	H. Herrlich, "Topologie II: Uniforme Räume" , Heldermann (1988)
[a18]	H. Herrlich, G. Salicrup, R. Vásquez, "Light factorization structures" Quest. Math. , 3 (1979) pp. 189–213
[a19]	H. Herrlich, G.E. Strecker, "Category theory" , Heldermann (1979)
[a20]	H. Hogbe-Nlend, "Théorie des bornologies et applications" , Lect. notes in math. , Springer (1971)
[a21]	M. Katětov, "On continuity structures and spaces of mappings" Comm. Math. Univ. Carolinae , 6 (1965) pp. 257–278
[a22]	C.J. Kelley, "Bitopological spaces" Proc. London Math. Soc. , 13 (1963) pp. 71–89
[a23]	D.C. Kent, "Convergence functions and their related topologies" Fund. Math. , 54 (1964) pp. 125–133
[a24]	H.-J. Kowalsky, "Limesräume und Komplettierung" Math. Nachr. , 12 (1954) pp. 301–340
[a25]	C. Kuratowski, "Sur l'opération 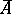de l'analysis situs" Fund. Math. , 3 (1922) pp. 182–199
[a26]	E.H. Moore, H.L. Smith, "A general theory of limits" Amer. J. Math. , 44 (1922) pp. 102–121
[a27]	G. Preuss, "Connectednesses and disconnectednesses in 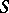-Near" , Categorical Aspects of Topology and Analysis , Lect. notes in math. , 915 , Springer (1982)
[a28]	G. Preuss, "Topological structures—An approach to categorical topology" , Reidel (1988)
[a29]	W. Reisig, "Petri nets" , EATCS Monographs on Theoretical Computer Science , 4 , Springer (1985)
[a30]	E.H. Spanier, "Algebraic topology" , Springer (1966)
[a31]	N.E. Steenrod, "A convenient category of topological spaces" Michigan Math. J. , 14 (1967) pp. 133–152
[a32]	J.W. Tukey, "Convergence and uniformity in topology" , Princeton Univ. Press (1940)
[a33]	A. Weil, "Sur les espaces à structure uniforme et sur la topologie générale" , Hermann (1937)
[a34]	O. Wyler, "Top categories and categorical topology" General Topol. Appl. , 1 (1971) pp. 17–28
[a35]	O. Wyler, "Are there topoi in topology?" , Categorical Topology , Lect. notes in math. , 540 , Springer (1976) pp. 699–719