Tate algebra
Let $ K $
be a field which is complete with respect to an ultrametric valuation $ | \cdot | $(
i.e. $ | x+ y | \leq \max ( | x | , | y | ) $).
The valuation ring $ R= \{ {a \in K } : {| a | \leq 1 } \} $
has a unique maximal ideal, $ m= \{ {a \in K } : {| a | < 1 } \} $.
The field $ k= R/m $
is called the residue field of $ K $.
Examples of such fields are the local fields, i.e. finite extensions of the $ p $- adic number field $ \mathbf Q _ {p} $, or the field of Laurent series $ \mathbf F _ {p} (( t)) $ in $ t $ with coefficients in the finite field $ \mathbf F _ {p} = \mathbf Z / p \mathbf Z $( cf. also Local field).
Let $ z _ {1} \dots z _ {n} $ denote indeterminates. Then $ T _ {n} ( K) = K \langle z _ {1} \dots z _ {n} \rangle $ denotes the algebra of all power series $ \sum a _ \alpha z _ {1} ^ {\alpha _ {1} } \dots z _ {n} ^ {\alpha _ {n} } $ with $ a _ \alpha \in K $( $ \alpha = ( \alpha _ {1} \dots \alpha _ {n} ) $) such that $ \lim\limits _ {| \alpha | \rightarrow \infty } a _ \alpha = 0 $( $ | \alpha | = \sum \alpha _ {i} $). The norm on $ T _ {n} = T _ {n} ( K) $ is given by $ \| \sum a _ \alpha z ^ \alpha \| = \max | a _ \alpha | $. The ring $ \{ {f \in T _ {n} } : {\| f \| \leq 1 } \} $ is denoted by $ T _ {n} ^ {o} $, and $ T _ {n} ^ {oo} = \{ {f \in T _ {n} } : {\| f \| < 1 } \} $ is an ideal of $ T _ {n} ^ {o} $. Then $ \widetilde{T} _ {n} = T _ {n} ^ {o} / T _ {n} ^ {oo} $ is easily seen to be the ring of polynomials $ k[ z _ {1} \dots z _ {n} ] $.
The $ K $- algebra $ T _ {n} ( K) $ is called the free Tate algebra. An affinoid algebra, or Tate algebra, $ A $ over $ K $ is a finite extension of some $ T _ {n} ( K) $( i.e. there is a homomorphism of $ K $- algebras $ T _ {n} \rightarrow A $ which makes $ A $ into a finitely-generated $ T _ {n} $- module). The space of all maximal ideals, $ \mathop{\rm Spm} ( A) $ of a Tate algebra $ A $ is called an affinoid space.
A rigid analytic space over $ K $ is obtained by glueing affinoid spaces. Every algebraic variety over $ K $ has a unique structure as a rigid analytic space. Rigid analytic spaces and affinoid algebras were introduced by J. Tate in order to study degenerations of curves and Abelian varieties over $ K $.
The theory of formal schemes over $ R $( the valuation ring of $ K $) is close to that of rigid analytic spaces. This can be seen as follows.
Fix an element $ \pi \in R $ with $ 0 < | \pi | < 1 $. The completion of $ R _ {n} = R[ z _ {1} \dots z _ {n} ] $ with respect to the topology given by the ideals $ \{ {\pi ^ {m} R _ {n} } : {m> 0 } \} $ is the ring of strict power series $ R\langle z _ {1} \dots z _ {n} \rangle $ over $ R $. Now $ R\langle z _ {1} \dots z _ {n} \rangle = T _ {n} ^ {o} $, and $ T _ {n} ( K) $ is the localization of $ R\langle z _ {1} \dots z _ {n} \rangle $ with respect to $ \pi $. So one can view $ \mathop{\rm Spm} ( T _ {n} ( K)) $ as the "general fibre" of the formal scheme $ \mathop{\rm Spf} ( R\langle z _ {1} \dots z _ {n} \rangle) $ over $ R $. More generally, any formal scheme $ X $ over $ R $ gives rise to a rigid analytic space over $ K $, the "general fibre" of $ X $. Non-isomorphic formal schemes over $ R $ can have the same associated rigid analytic space over $ K $. Further, any reasonable rigid analytic space over $ K $ is associated to some formal scheme over $ R $.
Affinoid spaces and affinoid algebras have many properties in common with affine spaces and affine rings over $ K $. Some of the most important are: Weierstrass preparation and division holds for $ T _ {n} ( K) $( cf. also Weierstrass theorem); affinoid algebras are Noetherian rings, and even excellent rings if the field $ K $ is perfect; for any maximal ideal $ M $ of an affinoid algebra $ A $ the quotient field $ R/M $ is a finite extension of $ K $; many finiteness theorems; any coherent sheaf $ S $ on an affinoid space $ \mathop{\rm Spm} ( A) $ is associated to a finitely-generated $ A $- module $ M= H ^ {0} ( S) $( further: $ H ^ {i} ( S)= 0 $ for $ i \neq 0 $).
Another interpretation of $ T _ {n} ( K) $ is: $ T _ {n} ( K) $ consists of all "holomorphic functions" on the polydisc $ \{ {( z _ {1} \dots z _ {n} ) \in K } : {\textrm{ all } | z _ {i} | \leq 1 } \} $. This interpretation is useful for finding the holomorphic functions on more complicated spaces like Drinfel'd's symmetric spaces $ \Omega ^ {(} n) $. Let $ K $ be a local field with algebraic closure $ \overline{K}\; $. Then
$$ \Omega ^ {(} n) = $$
$$ = \ \{ {( x _ {0} \dots x _ {n} ) \in P _ {\overline{K}\; } ^ {n} } : {\sum \lambda _ {i} x _ {i} \neq 0 \textrm{ for all } ( \lambda _ {0} \dots \lambda _ {n} ) \in P ^ {n} ( K) } \} $$
is a Drinfel'd symmetric space.
Spaces of this type have been used for the construction of Tate's elliptic curves (cf. Tate curve), Mumford curves and surfaces, Shimura curves and varieties, etc.
References
| [a1] | S. Bosch, U. Güntzer, R. Remmert, "Non-Archimedean analysis" , Springer (1984) |
| [a2] | V.G. Drinfel'd, "Coverings of 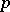 -adic symmetric regions" Funct. Anal. Appl. , 10 : 2 (1976) pp. 107–115 Funkts. Anal. Prilozhen. , 10 : 2 pp. 29–41 -adic symmetric regions" Funct. Anal. Appl. , 10 : 2 (1976) pp. 107–115 Funkts. Anal. Prilozhen. , 10 : 2 pp. 29–41 |
| [a3] | G. Faltings, "Arithmetische Kompaktifizierung des Modulraums der abelschen Varietäten" , Lect. notes in math. , 1111 , Springer (1984) |
| [a4] | J. Fresnel, M. van der Put, "Géométrie analytique rigide et applications" , Birkhäuser (1981) |
| [a5] | L. Gerritzen, M. van der Put, "Schottky groups and Mumford curves" , Lect. notes in math. , 817 , Springer (1980) |
| [a6] | D. Mumford, "An analytic construction of degenerating curves over complete local fields" Compos. Math. , 24 (1972) pp. 129–174 |
| [a7] | D. Mumford, "An analytic construction of degenerating abelian varieties over complete rings" Compos. Math. , 24 (1972) pp. 239–272 |
| [a8] | D. Mumford, "An algebraic surface with 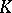 ample, ample, 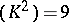 , , 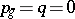 " Amer. J. Math. , 101 (1979) pp. 233–244 " Amer. J. Math. , 101 (1979) pp. 233–244 |
| [a9] | M. Raynaud, "Variétés abéliennes en géométrie rigide" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 2 , Gauthier-Villars (1971) pp. 473–477 |
| [a10] | J. Tate, "Rigid analytic spaces" Invent. Math. , 12 (1971) pp. 257–289 |
Tate algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tate_algebra&oldid=48949