Weierstrass theorem
There are a number of theorems named after Karl Theodor Wilhelm Weierstrass (1815-1897).
Infinite product theorem
Weierstrass' infinite product theorem [1]: For any given sequence of points in the complex plane $ \mathbf C $,
$$ \tag{1 } 0, \dots, 0 , \alpha _ {1} , \alpha _ {2}, \dots $$
$$ 0 < | \alpha _ {k} | \leq | \alpha _ {k+1} | ,\ k = 1, 2 , \dots ; \ \lim\limits _ {k \rightarrow \infty } | \alpha _ {k} | = \infty , $$
there exists an entire function with zeros at the points $ \alpha _ {k} $ of this sequence and only at these points. This function may be constructed as a canonical product:
$$ \tag{2 } W( z) = z ^ \lambda \prod _ { k= 1} ^ \infty \left ( 1- \frac{z}{\alpha _ {k} } \right ) e ^ {P _ {k} ( z) } , $$
where $ \lambda $ is the multiplicity of zero in the sequence (1), and
$$ P _ {k} ( z) = \frac{z}{\alpha _ {k} } + \frac{z ^ {2} }{2 \alpha _ {k} ^ {2} } + \dots + \frac{z ^ {m _ {k} } }{2 \alpha _ {k} ^ {m _ {k} } } . $$
The multipliers
$$ W \left ( \frac{z}{\alpha _ {k} } ; \ m _ {k} \right ) = \left ( 1- \frac{z}{\alpha _ {k} } \right ) e ^ {P _ {k} ( z) } $$
are called Weierstrass prime multipliers or elementary factors. The exponents $ m _ {k} $ are chosen so as to ensure the convergence of the product (2); for instance, the choice $ m _ {k} = k $ ensures the convergence of (2) for any sequence of the form (1).
It also follows from this theorem that any entire function $ f( z) $ with zeros (1) has the form
$$ f( z) = e ^ {g(z)} W( z) , $$
where $ W( z) $ is the canonical product (2) and $ g( z) $ is an entire function (see also Hadamard theorem on entire functions).
Weierstrass' infinite product theorem can be generalized to the case of an arbitrary domain $ D \subset \mathbf C $: Whatever a sequence of points $ \{ \alpha _ {k} \} \subset D $ without limit points in $ D $, there exists a holomorphic function $ f $ in $ D $ with zeros at the points $ \alpha _ {k} $ and only at these points.
The part of the theorem concerning the existence of an entire function with arbitrarily specified zeros may be generalized to functions of several complex variables as follows: Let each point $ \alpha $ of the complex space $ \mathbf C ^ {n} $, $ n \geq 1 $, be brought into correspondence with one of its neighbourhoods $ U _ \alpha $ and with a function $ f _ \alpha $ which is holomorphic in $ U _ \alpha $. Moreover, suppose this is done in such a way that if the intersection $ U _ \alpha \cap U _ \beta $ of the neighbourhoods of the points $ \alpha , \beta \in \mathbf C ^ {n} $ is non-empty, then the fraction $ f _ \alpha / f _ \beta \neq 0 $ is a holomorphic function in $ U _ \alpha \cap U _ \beta $. Under these conditions there exists an entire function $ f $ in $ \mathbf C ^ {n} $ such that the fraction $ f / f _ \alpha $ is a holomorphic function at every point $ \alpha \in \mathbf C ^ {n} $. This theorem is known as Cousin's second theorem (see also Cousin problems).
References
| [1] | K. Weierstrass, "Math. Werke" , 1–7 , Mayer & Müller (1894–1895) |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1 , Chelsea (1977) (Translated from Russian) MR0444912 Zbl 0357.30002 |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) Zbl 0578.32001 Zbl 0574.30001 |
Comments
References
| [a1] | R. Remmert, "Funktionentheorie" , II , Springer (1991) MR1150243 Zbl 0748.30002 |
Approximation of functions
Weierstrass' theorem on the approximation of functions: For any continuous real-valued function $ f( x) $ on the interval $ [ a, b] $ there exists a sequence of algebraic polynomials $ P _ {0} ( x), P _ {1} ( x), \dots $ which converges uniformly on $ [ a, b] $ to the function $ f( x) $; established by K. Weierstrass .
Similar results are valid for all spaces $ L _ {p} [ a, b] $. The Jackson theorem is a strengthening of this theorem.
The theorem is also valid for real-valued continuous $ 2 \pi $-periodic functions and trigonometric polynomials, e.g. for real-valued functions which are continuous on a bounded closed domain in an $ m $-dimensional space, or for polynomials in $ m $ variables. For generalizations, see Stone–Weierstrass theorem. For the approximation of functions of a complex variable by polynomials, see [3].
References
| [1a] | K. Weierstrass, "Über die analytische Darstellbarkeit sogenannter willkülicher Funktionen reeller Argumente" Sitzungsber. Akad. Wiss. Berlin (1885) pp. 633–639; 789–805 |
| [1b] | K. Weierstrass, "Über die analytische Darstellbarkeit sogenannter willkülicher Funktionen reeller Argumente" , Werke , 3 , Preuss. Akad. Wiss. (1903) |
| [2] | N.I. [N.I. Akhiezer] Achiezer, "Theory of approximation" , F. Ungar (1956) (Translated from Russian) |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) Zbl 0578.32001 Zbl 0574.30001 |
Yu.N. Subbotin
Comments
References
| [a1] | D. Gaier, "Vorlesungen über Approximation im Komplexen" , Birkhäuser (1980) MR0604011 Zbl 0442.30038 |
| [a2] | J. Wermer, "Banach algebras and several complex variables" , Springer (1976) MR0394218 Zbl 0336.46055 |
Uniformly convergent series of analytic functions
Weierstrass' theorem on uniformly convergent series of analytic functions : If the terms of a series
$$ \tag{* } s( z) = \ \sum _ { k= 0} ^ \infty u _ {k} ( z), $$
which converges uniformly on compacta inside a domain $ D $ of the complex plane $ \mathbf C $, are analytic functions in $ D $, then the sum $ s ( z) $ is an analytic function in $ D $. Moreover, the series
$$ \sum _ { k= 0} ^ \infty u _ {k} ^ {(m)} ( z) $$
obtained by $ m $ successive term-by-term differentiations of the series (*), for any $ m $, also converges uniformly on compacta inside $ D $ towards the derivative $ s ^ {(m)} ( z) $ of the sum of the series (*). This theorem has been generalized to series of analytic functions of several complex variables converging uniformly on compacta inside a domain $ D $ of the complex space $ \mathbf C ^ {n} $, $ n \geq 1 $, and the series of partial derivatives of a fixed order of the terms of the series (*) converges uniformly to the respective partial derivative of the sum of the series:
$$ \frac{\partial ^ {m} s( z) }{\partial z _ {1} ^ {m _ {1} } \dots \partial z _ {n} ^ {m _ {n} } } = \sum _ { k= 0} ^ \infty \frac{\partial ^ {m} u _ {k} ( z) }{\partial z _ {1} ^ {m _ {1} } \dots \partial z _ {n} ^ {m _ {n} } } , $$
$$ z = ( z _ {1}, \dots, z _ {n} ),\ m = m _ {1} + \dots + m _ {n} . $$
Weierstrass' theorem on uniform convergence on the boundary of a domain : If the terms of a series
$$ \sum _ { k= 0} ^ \infty u _ {k} ( z ) $$
are continuous in a closed bounded domain $ \overline{D} $ of the complex plane $ \mathbf C $ and are analytic in $ D $, then uniform convergence of this series on the boundary of the domain implies that it converges uniformly on the closed domain $ \overline{D} $.
This property of series of analytic functions is also applicable to analytic and harmonic functions defined, respectively, in a domain of the complex space $ \mathbf C ^ {n} $, $ n \geq 1 $, or in the Euclidean space $ \mathbf R ^ {n} $, $ n \geq 2 $. As a general rule it remains valid in all situations in which the maximum-modulus principle is applicable.
References
| [1a] | K. Weierstrass, "Abhandlungen aus der Funktionenlehre" , Springer (1866) |
| [1b] | K. Weierstrass, "Math. Werke" , 1–7 , Mayer & Müller (1894–1895) |
| [2] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , 1 , Cambridge Univ. Press (1952) pp. Chapt. 3 MR1424469 MR0595076 MR0178117 MR1519757 Zbl 0951.30002 Zbl 0108.26903 Zbl 0105.26901 Zbl 53.0180.04 Zbl 47.0190.17 Zbl 45.0433.02 Zbl 33.0390.01 |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) pp. Chapts. 3; 7 (Translated from Russian) MR0444912 Zbl 0357.30002 |
Comments
References
| [a1] | R. Remmert, "Theory of complex functions" , 1 , Springer (1990) (Translated from German) MR1084167 Zbl 0780.30001 |
Preparation theorem
Weierstrass' preparation theorem. A theorem obtained and originally formulated by K. Weierstrass in 1860 as a preparation lemma, used in the proofs of the existence and analytic nature of the implicit function of a complex variable defined by an equation $ f( z, w) = 0 $ whose left-hand side is a holomorphic function of two complex variables. This theorem generalizes the following important property of holomorphic functions of one complex variable to functions of several complex variables: If $ f( z) $ is a holomorphic function of $ z $ in a neighbourhood of the coordinate origin with $ f ( 0)= 0 $, $ f( z) \not\equiv 0 $, then it may be represented in the form $ f( z)= z ^ {s} g( z) $, where $ s $ is the multiplicity of vanishing of $ f( z) $ at the coordinate origin, $ s \geq 1 $, while the holomorphic function $ g( z) $ is non-zero in a certain neighbourhood of the origin.
The formulation of the Weierstrass preparation theorem for functions of $ n $ complex variables, $ n\geq 1 $. Let
$$ f( z) = f( z _ {1}, \dots, z _ {n} ) $$
be a holomorphic function of $ z=( z _ {1}, \dots, z _ {n} ) $ in the polydisc
$$ U = \{ {z } : {| z _ {i} | < a _ {i} , i= 1, \dots, n } \} , $$
and let
$$ f( 0) = 0 ,\ \ f( 0, \dots, 0, z _ {n} ) \not\equiv 0. $$
Then, in some polydisc
$$ V = \{ {z } : {| z _ {i} | < b _ {i} \leq a _ {i} ,\ i = 1, \dots, n } \} , $$
the function $ f( z) $ can be represented in the form
$$ f( z) = \ [ z _ {n} ^ {s} + f _ {1} ( z _ {1}, \dots, z _ {n-1} ) z _ {n} ^ {s-1} + \dots $$
$$ \dots {} + f _ {s} ( z _ {1}, \dots, z _ {n-1} )] g ( z) , $$
where $ s $ is the multiplicity of vanishing of the function
$$ f( z _ {n} ) = f ( 0, \dots, 0 , z _ {n} ) $$
at the coordinate origin, $ s \geq 1 $; the functions $ f _ {j} ( z _ {1}, \dots, z _ {n-1} ) $ are holomorphic in the polydisc
$$ V ^ \prime = \{ {( z _ {1}, \dots, z _ {n-1} ) } : { | z _ {i} | < b _ {i} , i = 1, \dots, n- 1 } \} , $$
$$ f _ {j} ( 0, \dots, 0) = 0,\ j = 1, \dots, s ; $$
the function $ g( z) $ is holomorphic and does not vanish in $ V $. The functions $ f _ {j} ( z _ {1}, \dots, z _ {n-1} ) $, $ j = 1, \dots, s $, and $ g( z) $ are uniquely determined by the conditions of the theorem.
If the formulation is suitably modified, the coordinate origin may be replaced by any point $ a=( a _ {1}, \dots, a _ {n} ) $ of the complex space $ \mathbf C ^ {n} $. It follows from the Weierstrass preparation theorem that for $ n> 1 $, as distinct from the case of one complex variable, every neighbourhood of a zero of a holomorphic function contains an infinite set of other zeros of this function.
Weierstrass' preparation theorem is purely algebraic, and may be formulated for formal power series. Let $ \mathbf C [[ z _ {1}, \dots, z _ {n} ]] $ be the ring of formal power series in the variables $ z _ {1}, \dots, z _ {n} $ with coefficients in the field of complex numbers $ \mathbf C $; let $ f $ be a series of this ring whose terms have lowest possible degree $ s\geq 1 $, and assume that a term of the form $ c z _ {n} ^ {s} $, $ c \neq 0 $, exists. The series $ f $ can then be represented as
$$ f = ( z _ {n} ^ {s} + f _ {1} z _ {n} ^ {s-1} + \dots + f _ {s} ) g, $$
where $ f _ {1}, \dots, f _ {s} $ are series in $ \mathbf C [[ z _ {1}, \dots, z _ {n-1} ]] $ whose constant terms are zero, and $ g $ is a series in $ \mathbf C [[ z _ {1}, \dots, z _ {n} ]] $ with non-zero constant term. The formal power series $ f _ {1}, \dots, f _ {s} $ and $ g $ are uniquely determined by $ f $.
A meaning which is sometimes given to the theorem is the following division theorem: Let the series
$$ f \in \mathbf C [ [ z _ {1}, \dots, z _ {n} ] ] $$
satisfy the conditions just specified, and let $ g $ be an arbitrary series in $ \mathbf C [[ z _ {1}, \dots, z _ {n} ]] $. Then there exists a series
$$ h \in \mathbf C [[ z _ {1}, \dots, z _ {n} ]] $$
and series
$$ a _ {j} \in \mathbf C [[ z _ {1}, \dots, z _ {n-1} ]] ,\ \ a _ {j} ( 0, \dots, 0) = 0, $$
$$ j = 0, \dots, s- 1, $$
which satisfy the following equation:
$$ g = hf + a _ {0} + a _ {1} z _ {n} + \dots + a _ {s-1} z _ {n} ^ {s-1} . $$
Weierstrass' preparation theorem also applies to rings of formally bounded series. It provides a method of inductive transition, e.g. from $ \mathbf C [[ z _ {1}, \dots, z _ {n-1} ]] $ to $ \mathbf C [[ z _ {1}, \dots, z _ {n} ]] $. It is possible to establish certain properties of the rings $ \mathbf C [ z _ {1}, \dots, z _ {n} ] $ and $ \mathbf C [[ z _ {1}, \dots, z _ {n} ]] $ in this way, such as being Noetherian and having the unique factorization property. There exists a generalization of this theorem to differentiable functions [6].
References
| [1a] | K. Weierstrass, "Abhandlungen aus der Funktionenlehre" , Springer (1866) |
| [1b] | K. Weierstrass, "Math. Werke" , 1–7 , Mayer & Müller (1894–1895) |
| [2] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1985) (In Russian) Zbl 0578.32001 Zbl 0574.30001 |
| [3] | S. Bochner, W.T. Martin, "Several complex variables" , Princeton Univ. Press (1948) MR0027863 Zbl 0041.05205 |
| [4] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) MR0180696 Zbl 0141.08601 |
| [5] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
| [6] | B. Malgrange, "Ideals of differentiable functions" , Tata Inst. (1966) MR2065138 MR0212575 Zbl 0177.17902 |
Comments
The polynomial
$$ z _ {n} ^ {s} + f _ {1} ( z _ {1}, \dots, z _ {n-1} ) z _ {n} ^ {s-1} + \dots + $$
$$ + f _ {s} ( z _ {1}, \dots, z _ {n-1} ) , $$
which occurs in the Weierstrass preparation theorem, is called a Weierstrass polynomial of degree $ s $ in $ z _ {n} $.
The analogue of the Weierstrass preparation theorem for differentiable functions is variously known as the differentiable preparation theorem, the Malgrange preparation theorem or the Malgrange–Mather preparation theorem. Let $ F $ be a smooth real-valued function on some neighbourhood of $ 0 $ in $ \mathbf R \times \mathbf R ^ {n} $ and let $ F( t, 0) = g( t) t ^ {k} $ with $ g( 0) \neq 0 $ and $ g $ smooth near $ 0 $ in $ \mathbf R $. Then the Malgrange preparation theorem says that there exists a smooth function $ q $ near zero such that $ ( q F )( t, x) = t ^ {k} + \sum _ {i=0} ^ {k-1} \lambda _ {i} ( x ) t ^ {i} $ for suitable smooth $ \lambda _ {i} $, and the Mather division theorem says that for any smooth $ G $ near $ 0 $ in $ \mathbf R \times \mathbf R ^ {n} $ there exist smooth functions $ q $ and $ r $ on $ \mathbf R \times \mathbf R ^ {n} $ near $ 0 $ such that $ G = q F + r $ with $ r( t, x) = \sum _ {i=0} ^ {k-1} r _ {i} ( x) t ^ {i} $. For more sophisticated versions of the differentiable preparation and division theorems, cf. [a2]–[a4].
An important application is the differentiable symmetric function theorem (differentiable Newton theorem), which says that a germ $ f $ of a symmetric differentiable function of $ x _ {1}, \dots, x _ {n} $ in $ 0 $ can be written as a germ of a differentiable function in the elementary symmetric functions $ \sigma _ {1} = x _ {1} + \dots + x _ {n} $, $ \sigma _ {n} = x _ {1}, \dots, x _ {n} $, [a7], [a8].
There exist also $ p $-adic analogues of the preparation and division theorems. Let $ k $ be a complete non-Archimedean normed field (cf. Norm on a field). $ T _ {n} ( k) = k \langle z _ {1}, \dots, z _ {n} \rangle $ is the algebra of power series $ \sum a _ \alpha z ^ \alpha $, $ \alpha = ( \alpha _ {1}, \dots, \alpha _ {n} ) $, $ \alpha _ {i} \in \mathbf N \cup \{ 0 \} $, $ z ^ \alpha = z _ {1} ^ {\alpha _ {1} }, \dots, z _ {n} ^ {\alpha _ {n} } $, such that $ | a _ \alpha | \rightarrow 0 $ as $ | \alpha | \rightarrow \infty $, $ | \alpha | = \alpha _ {1} + \dots + \alpha _ {n} $. The norm on $ T _ {n} ( k) $ is defined by $ \| \sum a _ \alpha z ^ \alpha \| = \max _ \alpha | a _ \alpha | $. The subring $ A _ {n} ( k) $ consists of all $ f \in T _ {n} ( k) $ with $ \| f \| \leq 1 $ and $ \mathfrak m _ {n} ( k) $ is the ideal of all $ f \in A _ {n} ( k) $ with $ | f | < 1 $. Let $ \overline{T} _ {n} ( k) $ be the residue ring $ A _ {n} ( k)/ \mathfrak m _ {n} ( k) $, and let $ f \mapsto \overline{f} $ be the quotient mapping. Then $ \overline{T} _ {n} ( k) = \overline{k} [ z _ {1} \dots z _ {n} ] $, where $ \overline{k} $ is the residue field of $ k $. An element $ f \in T _ {n} ( k) $ with $ \| f \| = 1 $ is called regular in $ z _ {n} $ of degree $ d $ if $ \overline{f} $ is of the form $ \overline{f} = \lambda z _ {n} ^ {d} + \sum _ {i=0} ^ {d-1} c _ {i} z _ {n} ^ {i} $ with $ c _ {i} \in \overline{k} [ z _ {1}, \dots, z _ {n-1} ] $ and $ 0 \neq \lambda \in \overline{k} $. Note that $ T _ {n-1} ( k) [ z _ {n} ] = k \langle z _ {1}, \dots, z _ {n-1} \rangle [ z _ {n} ] $ is naturally a subalgebra of $ T _ {n} ( k) $. The $ p $-adic Weierstrass preparation and division theorem now says: i) (division) Let $ F \in T _ {n} ( k) $ be regular of degree $ d $ in $ z _ {n} $ and let $ G \in T _ {n} ( k) $. Then there exist unique elements $ q \in T _ {n} ( k) $ and $ r _ {i} \in T _ {n-1} ( k) $, $ i = 0, \dots, d- 1 $, such that $ G = qF + \sum _ {i=0} ^ {d-1} r _ {i} z _ {n} ^ {i} $ and, moreover, $ \| G \| = \max ( \| F \| , r ) $, where $ r = \sum _ {i=0} ^ {d-1} r _ {i} z _ {n} ^ {i} $; ii) (preparation) Let $ F \in T _ {n} ( k) $ be of norm $ 1 $, then there exists a $ k $-automorphism of $ T _ {n} ( k) $ such that $ \sigma ( F ) $ is regular in $ z _ {n} $.
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4 MR0344507 Zbl 0271.32001 |
| [a2] | M. Golubitsky, "Stable mappings and their singularities" , Springer (1973) pp. Chapt. IV MR0341518 Zbl 0294.58004 |
| [a3] | J.C. Tougeron, "Ideaux de fonction différentiables" , Springer (1972) pp. Chapt. IX MR0440598 |
| [a4] | B. Malgrange, "Ideals of differentiable functions" , Oxford Univ. Press (1966) pp. Chapt. V MR2065138 MR0212575 Zbl 0177.17902 |
| [a5] | J. Fresnel, M. van der Put, "Géométrie analytique rigide et applications" , Birkhäuser (1981) pp. §II.2 MR0644799 Zbl 0479.14015 |
| [a6] | N. Koblitz, "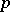 -adic numbers, -adic numbers, 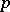 -adic analysis, and zeta-functions" , Springer (1977) pp. 97 MR466081 -adic analysis, and zeta-functions" , Springer (1977) pp. 97 MR466081 |
| [a7] | G. Glaeser, "Fonctions composés différentiables" Ann. of Math. , 77 (1963) pp. 193–209 |
| [a8] | S. Łojasiewicz, "Whitney fields and the Malgrange–Mather preparation theorem" C.T.C. Wall (ed.) , Proc. Liverpool Singularities Symposium I , Lect. notes in math. , 192 , Springer (1971) pp. 106–115 Zbl 0224.58003 |
Weierstrass theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_theorem&oldid=52097