Tactical configuration
$ t $-design, $ t $-$ ( v, k, \lambda ) $-design on a $ v $-set $ S $
A $ t $-design is a system of $ k $-subsets (blocks) of the set $ S $ such that every $ t $-subset of elements of $ S $ appears in exactly $ \lambda $ blocks. The class of $ 2 $-designs coincides with the class of balanced incomplete block designs (cf. Block design). The name tactical configuration is given to an incidence system in which every set is incident with exactly $ k $ elements, while every element is incident with exactly $ r $ sets. A $ t $-design with $ t = k $ is called trivial. If a $ t $-design is not trivial, then
$$ t + 1 \leq k \leq v - 1 - t. $$
Every $ t $-design is an $ s $-design for any $ s \leq t $. The number $ \lambda _ {s} $ of occurrences of an arbitrary $ s $-subset in the blocks of a $ t $-design is given by the formula
$$ \lambda _ {s} = \ \left ( \begin{array}{c} k - s \\ t - s \end{array} \right ) ^ {-1} \left ( \begin{array}{c} v - s \\ t - s \end{array} \right ) \lambda ,\ \ 0 < s \leq t. $$
The condition that the $ \lambda _ {s} $ be integers is a necessary condition for the existence of a $ t $-design. In particular, for $ t \geq 2 $ every $ t $-design is a balanced incomplete block design.
The main question concerning $ t $-designs is the problem of their existence and construction. For a long time, for $ t > 3 $ only isolated examples were known; in particular $ 5 $-$ ( 12, 6, 1) $- and $ 5 $-$ ( 24, 8, 1) $-designs connected with the five-fold transitive Mathieu groups $ M _ {12} $ and $ M _ {24} $ (cf. Mathieu group), respectively. However, in the 1960s the connection between $ t $-designs and coding theory (cf. Code) was discovered (see, for example, [3] and [4]), and, starting from vectors with $ v $ non-zero coordinates, a way was shown of constructing a $ t $-design belonging to a linear $ ( n, k) $-code, which is a $ k $-dimensional vector subspace of an $ n $-dimensional space over a finite field (see [5] and [7]).
It is well known that $ t $-fold transitive groups other than the symmetric and the alternating groups lead to non-trivial $ t $-designs; this yields a few infinite series of $ 3 $-designs. With the help of ideas from group theory and geometry, infinite classes of $ 4 $- and $ 5 $-designs were also constructed (see for example [6]).
For the number $ b $ of blocks in a $ t $-design there is the inequality
$$ \tag{* } b \geq \ \left \{ \begin{array}{ll} \left ( \begin{array}{c} v \\ s \end{array} \right ) & \textrm{ if } t = 2s, v \geq k + s, \\ 2 \left ( \begin{array}{c} v - 1 \\ s \end{array} \right ) & \textrm{ if } t = 2s + 1, v - 1 \geq k + s, \\ \end{array} \right. $$
generalizing the Fisher inequality $ ( b \geq v) $ for balanced incomplete block designs. In the case of equality in (*), the $ t $-design is called tight. Tight $ t $-designs generalize symmetric $ 2 $-designs; in particular, for $ t = 2s $ the set of intersection numbers of blocks in a tight $ t $-design contains exactly $ s $ different elements.
The tight $ 3 $-designs are the Hadamard designs, i.e. they are the $ 3 $-$ ( 4n, 2n, n- 1) $-designs, while for $ s \geq 2 $ there are no non-trivial tight $ ( 2s + 1) $-designs. From a given $ t $-$ ( v, k, \lambda ) $-design three other $ t $-designs can be obtained: a) taking the complement in $ S $ of each block; b) discarding an arbitrary element and all the blocks that contain it; and c) taking blocks containing an arbitrarily chosen element and removing it from them. The $ t $-designs thus obtained are called, respectively, the complementary, the residual and the derived $ t $-design with respect to the initial one. They are, respectively, a $ t $-$ ( v, v- k, \lambda ^ {c} ) $-design with
$$ \lambda ^ {c} = \ \left ( \begin{array}{c} k \\ t \end{array} \right ) ^ {-1} \left ( \begin{array}{c} v - k \\ t \end{array} \right ) \lambda , $$
a $ ( t - 1) $-$ ( v- 1, k, \lambda ^ {r} ) $-design with
$$ \lambda ^ {r} = ( v - k) ( k - t + 1) ^ {-1} \lambda $$
and a $ ( t - 1) $-$ ( v- 1, k- 1, \lambda ) $-design.
References
| [1] | R. Dembowski, "Finite geometries" , Springer (1968) pp. 254 |
| [2] | D.K. Ray-Chaudhuri, R.M. Wilson, "On t-designs" Osaka J. Math. , 12 (1975) pp. 737–744 |
| [3] | E.F. Assmus, H.F. Mattson, "Perfect codes and the Mathieu groups" Arch. Math. Basel , 17 (1966) pp. 121–135 |
| [4] | E.F. Assmus, H.F. Mattson, "New 5-designs" J. Comb. Theory , 6 (1969) pp. 122–151 |
| [5] | N.V. Semakov, V.A. Zinov'ev, "Balanced codes and tactical configurations" Problems Inform. Transmission , 5 : 3 (1969) pp. 22–28 Probl. Peredachi Inform. , 5 : 3 (1969) pp. 28–36 |
| [6] | W.O. Alltop, "An infiite class of 5-designs" J. Comb. Theory , 12 (1972) pp. 390–395 |
| [7] | V. Pless, "Symmetry codes over GF(3) and new five-designs" J. Comb. Theory , 12 (1972) pp. 119–142 |
Comments
A $ t $-$ ( v , k, \lambda ) $-design with $ \lambda = 1 $ is also known as a Steiner system and denoted by $ S( t, k, v ) $; an arbitrary $ t $-$ ( v, k, \lambda ) $-design is sometimes denoted $ S _ \lambda ( t, k, v) $.
Of particular interest is the existence of non-trivial $ t $-designs without repeated blocks (i.e. no $ k $-subset appears twice in the list of blocks); such $ t $-designs are called simple. L. Teirlinck [a3] settled a long-standing conjecture by proving the existence of non-trivial simple $ t $-designs for every value of $ t $. A list of the known infinite families of simple $ t $-designs with $ t \geq 4 $ and a table of simple $ t $-designs with $ v \leq 30 $ is given in [a4].
The only non-trivial tight $ 4 $-design is the unique $ 4 $-$ ( 23, 7, 1) $-design related to the Mathieu group $ M _ {23} $ (see [a5]–[a7]), and there are only finitely many tight $ 2s $-designs for any fixed value $ s \geq 5 $ (see [a8]).
References
| [a1] | F.J. MacWilliams, N.J.A. Sloane, "The theory of error-correcting codes" , I-II , North-Holland (1978) |
| [a2] | T. Beth, D. Jungnickel, H. Lenz, "Design theory" , Cambridge Univ. Press (1986) |
| [a3] | L. Teirlinck, "Non-trivial 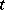 -designs without repeated blocks exist for all -designs without repeated blocks exist for all 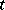 " Disc. Math. , 65 (1987) pp. 301–311 " Disc. Math. , 65 (1987) pp. 301–311 |
| [a4] | Y.M. Chee, C.J. Colbourn, D.L. Kreher, "Simple 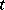 -designs with -designs with 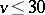 " Ars Comb. , 29 (1990) pp. 193–258 " Ars Comb. , 29 (1990) pp. 193–258 |
| [a5] | N. Ito, "Tight 4-designs" Osaka J. Math. , 12 (1975) pp. 493–522 |
| [a6] | H. Enomoto, N. Ito, R. Noda, "Tight 4-designs" Osaka J. Math. , 16 (1979) pp. 353–356 |
| [a7] | A. Bremner, "A diophantine equation arising from tight 4-designs" Osaka J. Math. , 16 (1979) pp. 353–356 |
| [a8] | E. Bannai, "On tight designs" Quart. J. Math. (Oxford) , 28 (1977) pp. 433–448 |
| [a9] | M. Hall, "Combinatorial theory" , Blaisdell (1967) |
Tactical configuration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tactical_configuration&oldid=52231