System of subvarieties
system of submanifolds
Given a differentiable manifold (or algebraic variety) $ M $, a system of submanifolds (system of subvarieties) is a differentiably (algebraically) parametrized family of submanifolds (subvarieties) $ \{ N _ \lambda \} $. More generally, the notion makes sense and is useful also for other geometric objects, such as complex spaces, topological manifolds, algebras, etc. Such systems occur in may parts of mathematics both as tools and as objects to be investigated. Often additional requirements are added.
1. Foliations.
A codimension- $ k $ foliation of a differentiable manifold $ M $ is a $ k $- dimensional system of submanifolds of dimension $ n- k $ such that locally near every point in $ M $ the system looks like the system of parallel translates of $ \mathbf R ^ {n-} k $ in $ \mathbf R ^ {n} $. Cf. Foliation for more details.
2. Nets.
A net in differential geometry is a family of $ n $ $ ( n- 1) $- parameter systems of smooth curves $ \{ \sigma ^ {1} \dots \sigma ^ {n} \} $ on an $ n $- dimensional manifold $ M $ such that through each point there passes precisely one curve from each family and such that the $ n $ curves passing through a point $ x $ intersect transversally (i.e. their tangent vectors at $ x $ span the whole tangent space $ T _ {x} M $). Cf. Net (in differential geometry). Thus, a net consists so to speak of $ n $ transversally intersecting codimension- $ ( n- 1) $ foliations.
3. Webs.
More generally one can consider $ m $" transversally intersecting" foliations of codimension $ k $ of an $ n $- dimensional manifold for more general $ k $, $ m $, $ n $. This leads to the theory of webs, cf. Webs, geometry of and [a13].
4. Linear systems.
When the subvarieties or submanifolds are given by equations, e.g. in $ \mathbf C ^ {n} $ or in $ P ^ {n} ( \mathbf C ) $, it makes sense to talk about linear systems. A linear system of subvarieties is given by a family of equations
$$ \tag{* } \lambda _ {0} F _ {1} + \dots + \lambda _ {m} F _ {m} = 0, $$
where the $ F _ {i} $ are functions on the ambient manifold. Cf. also Linear system. The notion of a linear algebraic system has received a great deal of attention particularly in analytic, projective and algebraic geometry, e.g. in the form of a (linear) system of subvarieties of a variety $ M \subset P ^ {n} ( \mathbf C ) $" cut out" by the system (*). Often the varieties in a linear system are all of the same dimension, or even of the same kind (apart from non-generic degeneracies).
5. Web (in algebraic geometry).
A three- (or higher-) parameter linear system of varieties, i.e. $ m= 3 $ in (*). Sometimes also called a net.
6. Net (in algebraic geometry).
A two-parameter linear system of varieties, i.e. $ m= 2 $ in (*). Cf. Net for more details.
7. Pencil (in geometry).
By far the most attention has been paid to one-dimensional systems of varieties and manifolds. These are called pencils. Thus, the family of curves in the plane determined by
$$ \lambda _ {1} F _ {1} + \lambda _ {2} F _ {2} = 0 $$
for all possible values of the parameters $ \lambda _ {1} $ and $ \lambda _ {2} $( except $ \lambda _ {1} = 0 $, $ \lambda _ {2} = 0 $) is a pencil (in fact, the pencil depends on the single parameter $ \lambda _ {1} : \lambda _ {2} $). The equation of a pencil of surfaces in space is written similarly. The two equations $ F _ {1} = 0 $ and $ F _ {2} = 0 $ give two elements of the pencil (two curves or two surfaces) which determine the whole pencil. Every two elements of the pencil intersect in the same set of points — the support. The support of the pencil can contain real as well as imaginary points. If the original curves of the pencil are algebraic curves of orders $ m $ and $ n $, then the support consists of $ mn $ points (real or imaginary, ordinary or exceptional, cf. Bezout theorem).
A pencil of straight lines is the set of all straight lines lying in a plane and passing through a fixed point (an ordinary pencil) or parallel to a fixed straight line (an exceptional pencil). The equation of a pencil of straight lines has the form
$$ \lambda _ {1} ( A _ {1} x + B _ {1} y + C _ {1} ) + \lambda _ {2} ( A _ {2} x + B _ {2} y + C _ {2} ) = 0. $$
A pencil of planes is the set of all planes passing through a fixed straight line (an ordinary pencil) or parallel to a certain fixed plane (an exceptional pencil). The equation of a pencil of planes has the form
$$ \lambda _ {1} ( A _ {1} x + B _ {1} y + C _ {1} z + D _ {1} ) + \lambda _ {2} ( A _ {2} x + B _ {2} y + C _ {2} z + D _ {2} ) = 0. $$
A pencil of circles is a one-parameter family of circles which linearly depends on the parameter. A pencil of circles contains circles and one straight line. The support of an (ordinary) pencil of circles consists of the two circular points and two ordinary points $ a $ and $ b $. If $ a \neq b $, then a pencil of circles can be defined as the set of circles (taking straight lines as circles of infinite radius) which pass through the points $ a $ and $ b $; if $ a = b $ it is necessary to require in addition that the circles all touch at the point $ a $. If $ a $ and $ b $ are real and distinct, the pencil of circles is said to be elliptic (Fig. a), if they coincide (and are real) it is called parabolic (Fig. b) and if they are imaginary (and distinct) it is said to be hyperbolic (Fig. c). A set of concentric circles (Fig. d) is an exceptional pencil.
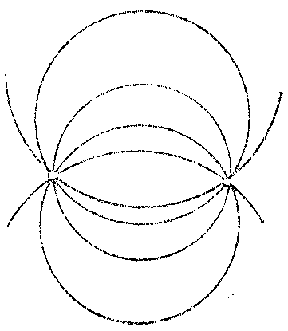
Figure: s091970a
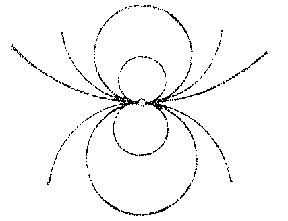
Figure: s091970b
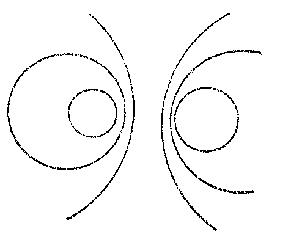
Figure: s091970c
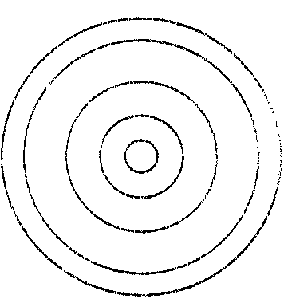
Figure: s091970d
Every ordinary pencil of circles has a so-called radical axis — a straight line each point of which has the same power (different for different points) with respect to all circles of the pencil (cf. Degree of a point). The radical axis of an elliptic pencil passes through the common points of the circles; for a parabolic pencil it is their common tangent; for a hyperbolic pencil it is the line joining the centres of the two circles which are orthogonal to all the circles of the pencil. The centres of the circles of a pencil lie on a straight line which is perpendicular to the radical axis. The point of intersection of the line of the centres of a pencil and its radical axis is called the centre of the pencil. The power of the centre of the pencil with respect to any circle of the pencil is the same and is called the power of the pencil. If the $ x $- axis is the line of centres of the circles of the pencil, and the $ y $- axis is the radical axis of the pencil, then the equation of an arbitrary circle of the pencil has the form
$$ x ^ {2} + y ^ {2} - 2xt + p = 0, $$
where $ t $ is the parameter determining a given circle and $ p $ is the power of the pencil. For an elliptic pencil $ p < 0 $, for a parabolic pencil $ p = 0 $, for a hyperbolic pencil $ p > 0 $( the power of an exceptional pencil can be considered to be infinite).
The circles which are orthogonal to all the circles of a given pencil form a pencil themselves; this pencil is said to be conjugate to the given pencil. An elliptic pencil is conjugate to a hyperbolic pencil and a parabolic pencil is conjugate to a parabolic pencil.
Any pencil of circles is the intersection of two nets (cf. Net) of circles.
A pencil of spheres is a one-parameter family of spheres which linearly depends on the parameter. Any two spheres of the pencil intersect in a circle of real, zero or imaginary radius. In the first case the pencil of spheres is said to be elliptic, it consists of all spheres passing through a given circle; in the second case it is parabolic, and the pencil consists of all the spheres touching at a common point; in the third case it is hyperbolic, and the pencil consists of all the spheres which are orthogonal to three given spheres which intersect at two points. A pencil of spheres has a so-called radical plane, each point of which has the same power (different for different points) with respect to all the spheres of the pencil; the centres of all the spheres of a pencil lie on a single straight line, which is perpendicular to the radical plane.
A pencil of spheres is the intersection of three nets of spheres with centres lying on a single straight line.
In projective geometry an algebraic pencil of lines is the set of all lines in the projective plane with coordinates $ u _ {1} , u _ {2} , u _ {3} $ satisfying the equation
$$ F ( u _ {1} , u _ {2} , u _ {3} ) = 0, $$
where $ F ( u _ {1} , u _ {2} , u _ {3} ) $ is a polynomial not identically zero and homogeneous with respect to the variables $ u _ {1} $, $ u _ {2} $ and $ u _ {3} $; the degree of $ F $ is called the degree (or order) of the pencil of lines. A first-order algebraic pencil of lines is given by an equation
$$ a _ {1} u _ {1} + a _ {2} u _ {2} + a _ {3} u _ {3} = 0 $$
and is the set of all lines passing through the point with coordinates $ ( a _ {1} , a _ {2} , a _ {3} ) $.
A second-order algebraic pencil of lines is given by an equation
$$ f _ {11} u _ {1} ^ {2} + f _ {22} u _ {2} ^ {2} + f _ {33} u _ {3} ^ {2} + 2f _ {12} u _ {1} u _ {2} + 2f _ {13} u _ {1} u _ {3} + $$
$$ + 2f _ {23} u _ {2} u _ {3} = 0,\ f _ {ij} = f _ {ji} ,\ i, j = 1, 2, 3, $$
where the $ f _ {ij} $ are real numbers at least one of which is non-zero. If the discriminant $ \delta = | f _ {ij} | $, $ i = 1, 2, 3 $, is non-zero, the second-order pencil of lines is called non-degenerate, if $ \delta = 0 $ it is degenerate. Each non-degenerate second-order pencil is the set of tangents to a non-degenerate second-order curve; each non-degenerate second-order curve is the envelope of a certain non-degenerate pencil of the second order.
More assorted algebraic and geometric pencils are discussed in Lobachevskii geometry; Darboux quadric; Halphen pencil; Cubic; Monodromy transformation; Circle.
Note that in some of the literature dealing with webs, nets and pencils in the sense of $ \geq 3 $-, $ 2 $- and $ 1 $- dimensional families one occasionally adds the requirement that through each point there pass precisely a given number of members of the system, while the linearity condition (*) is dropped. Cf. e.g. [a14].
8. Fibrations.
Let $ \{ N _ \lambda \} _ {\lambda \in \Lambda } $ be a system of submanifolds or subvarieties such that through each of the points of the ambient manifold $ M $ there passes exactly one of the $ N _ \lambda $. Then there results a mapping $ M \rightarrow \Lambda $. A priori, this mapping need not even be continuous. But if $ M \rightarrow \Lambda $ has appropriate properties (e.g. differentiable, holomorphic, algebraic, depending on the kind of objects under consideration), one obtains a fibration. Conversely, a surjective mapping $ \pi : M \rightarrow B $ defines a system $ \{ \pi ^ {- 1 } ( b) \} _ {b \in B } $. If the fibration is locally trivial, i.e. if locally in $ B $ the mapping $ \pi $ looks like $ U \times F \rightarrow U $, one usually speaks of a fibre bundle instead of a fibration.
9. Pencils of matrices.
The word "pencil" is also used in other fields of mathematics, to denote one-parameter (linear) families of objects. Thus, one speaks of pencils of operators $ \lambda A + \mu B $, and especially of pencils of matrices $ \lambda A + \mu B $, or, inhomogeneously, $ A + \lambda B $. The pencil $ A + \lambda B $, where $ A $ and $ B $ have coefficients in a field $ K $, can also be regarded as a matrix over $ K[ \lambda ] $.
Two polynomial matrices $ M _ {1} ( \lambda ) $, $ M _ {2} ( \lambda ) $, i.e. matrices with coefficients in $ K[ \lambda ] $, are equivalent if there are invertible matrices $ P( \lambda ) $, $ Q( \lambda ) $ such that $ P ( \lambda ) M _ {1} ( \lambda ) Q ( \lambda ) = M _ {2} ( \lambda ) $. (Note that a square matrix $ P ( \lambda ) $ over $ K [ \lambda ] $ is invertible if and only if its determinant is a non-zero element of the field of constants $ K $.) The two polynomial matrices are strictly equivalent if there are invertible matrices $ S $, $ T $ over $ K $ such that $ SM _ {1} ( \lambda ) T= M _ {2} ( \lambda ) $. Equivalence of matrices is described precisely by the Smith canonical form, cf. Normal form for more details.
Consider a pencil of square matrices $ A + \lambda B $ such that $ \mathop{\rm det} ( B) \neq 0 $. For such pencils strict equivalence is the same as equivalence. A pencil of matrices is called regular if $ \mathop{\rm det} ( A+ \lambda B) $ does not vanish identically. All other pencils are called singular.
The theory of invariants and canonical form for pencils of matrices was developed by L. Kronecker [a10]; cf. also [a9] for a complete account and some applications.
In (automatic) linear control theory one studies linear control systems
$$ \dot{x} = Ax+ Bu,\ x \in \mathbf R ^ {n} ,\ u \in \mathbf R ^ {m} , $$
determined by a pair of matrices $ ( A, B) $ over $ \mathbf R $( or $ \mathbf C $) of sizes $ n \times n $ and $ n \times m $, respectively. The so-called feedback group is generated by the following transformations:
$$ ( A, B) \mapsto ( A, BT) ,\ T \in \mathop{\rm GL} _ {m} ( \mathbf R ) $$
(this corresponds to a base change in the space $ \mathbf R ^ {m} $ of controls);
$$ ( A, B) \mapsto ( SAS ^ {-} 1 , SB) ,\ S \in \mathop{\rm GL} _ {n} ( \mathbf R ) $$
(this corresponds to a base change in the state space $ \mathbf R ^ {n} $);
$$ ( A, B) \mapsto ( A + BF , B) ,\ F \in \mathbf R ^ {m \times n } $$
(this corresponds to state feedback: $ u \mapsto u+ Fx $).
Associate to the linear control system $ ( A, B) $ the singular pencil
$$ \tag{** } ( B, - \lambda I + A ) $$
of $ n \times ( n+ m) $ matrices. Now observe, [a2], that two pencils of the form (**) are strictly equivalent if and only if the corresponding control systems are equivalent under the feedback group.
The control system $ ( A, B) $ is completely reachable if the columns of the $ A ^ {i} B $, $ i= 0, 1 \dots $ span all of $ \mathbf R ^ {n} $. For pencils of the form (**) of completely-reachable control systems, many of the Kronecker invariants for pencils vanish; the most important that remain are a finite number of integer-valued ones. These can be described as follows. Let $ \mu _ {i} $ be the dimension of the space spanned by the columns of $ B, AB \dots A ^ {i-} 1 B $, $ i= 1, 2 ,\dots $. Let $ \nu _ {i} = \mu _ {i} - \mu _ {i-} 1 $, $ i= 1, 2 \dots $ $ \mu _ {0} = 0 $. Then $ \nu _ {1} \geq \nu _ {2} \geq \dots $, and $ \nu _ {i} = 0 $ for $ i> n $. Now, let $ \kappa _ {1} \dots \kappa _ {m} $ be the dual partition of the partition $ ( \nu _ {1} \dots \nu _ {n} ) $ of $ n $, i.e. $ \kappa _ {i} = \# \{ j : \nu _ {j} \geq i \} $. (Note that $ \kappa _ {i} = 0 $ for $ i> m $, because $ \nu _ {1} \leq m $.) These $ \kappa _ {1} \dots \kappa _ {m} $ are potentially non-zero Kronecker invariants of (**). They are called the Kronecker indices in control theory. There is a corresponding state-feedback canonical form for a completely-reachable pair $ ( A, B) $ in which the matrix $ A $ is a Jordan matrix with Jordan blocks $ Jx _ {i} ( 0) $, $ i= 1 \dots m $, while $ B $ consists of standard unit vectors $ e _ {r _ {i} } $, $ r _ {i} = \kappa _ {1} + \dots + \kappa _ {i} $, and, possibly, other vectors. This canonical form is called the Brunovsky canonical form. See [a12] and, e.g., [a11] for related matters.
10. Deformations (in algebra, algebraic, analytic and differential geometry, etc.).
Still another way of looking at a family of (sub) manifolds or varieties (or other structures) is as a deformation.
Note on terminology.
The terminology "web" , "net" , "pencil" as in 5.–7. above for, respectively, $ \geq 3 $-, $ 2 $- and $ 1 $- dimensional (linear) systems is not completely standard. In particular, one also finds "net" instead of "web" , and sometimes "bundle" in the meaning of both "net" (as in 6.) and "pencil" (as in 7. or, rarely, as in 9.).
The material in 7. above is basically a translation of the subsection on pencils by A.B. Ivanov appearing under "puchok" in the original Russian version of the Encyclopaedia. The remainder of this article is original to this annotated and expanded translation.
References
| [a1] | M.M. Postnikov, "Analytic geometry" , Moscow (1973) (In Russian) MR0987205 MR0890748 Zbl 0662.51001 Zbl 0482.51001 |
| [a2] | J.L. Coolidge, "A treatise on the circle and the sphere" , Chelsea, reprint (1971) MR0389515 Zbl 0251.50002 |
| [a3] | S.-T. Hu, "Differentiable manifolds" , Holt, Rinehart & Winston (1969) MR0245030 Zbl 0182.26102 |
| [a4] | J. Morrow, K. Kodaira, "Complex manifolds" , Holt, Rinehart & Winston (1971) MR0302937 Zbl 0325.32001 |
| [a5] | M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French) MR0903026 MR0895392 MR0882916 MR0882541 Zbl 0619.53001 Zbl 0606.51001 Zbl 0606.00020 |
| [a6] | J. Coolidge, "A history of the conic sections and quadratic surfaces" , Dover, reprint (1968) Zbl 0202.00103 |
| [a7] | H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) MR1531486 MR0123930 Zbl 0095.34502 |
| [a8] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) MR0507725 Zbl 0408.14001 |
| [a9] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 2 , Chelsea, reprint (1959) pp. Chapt. XII (Translated from Russian) MR0107649 MR0107648 Zbl 0085.01001 |
| [a10] | L. Kronecker, "Algebraische Reduktion der Schaaren bilinearer Formen" Sitzungsber. Akad. Berlin (1890) pp. 763–776 |
| [a11] | M. Hazewinkel, "A partial survey of the uses of algebraic geometry in system and control theory" , Symp. Math. INDAM (Rome 1979) , 24 , Acad. Press (1981) pp. 245–292 MR0619251 |
| [a12] | R.E. Kalman, "Kronecker invariants and feedback" L. Weiss (ed.) , Ordinary Differential Equations , Acad. Press (1972) pp. 459–471 MR0421751 Zbl 0308.93008 |
| [a13] | V.V. Goldberg, "Theory of multicodimensional webs" , Kluwer (1988) Zbl 0668.53001 |
| [a14] | F. Severi, "Vorlesungen über algebraische Geometrie" , Johnson, reprint (1968) MR0245574 Zbl 48.0687.01 |
System of subvarieties. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=System_of_subvarieties&oldid=48944