Lobachevskii geometry

A geometry based on the same fundamental premises as Euclidean geometry, except for the axiom of parallelism (see Fifth postulate). In Euclidean geometry, according to this axiom, in a plane through a point $ P $ not lying on a straight line $ A ^ \prime A $ there passes precisely one line $ B ^ \prime B $ that does not intersect $ A ^ \prime A $. The line $ B ^ \prime B $ is called a parallel to $ A ^ \prime A $. It is sufficient to require that there is at most one straight line, since the existence of a non-intersecting line can be proved by successively drawing lines $ PQ \perp A ^ \prime A $ and $ PB \perp PQ $.

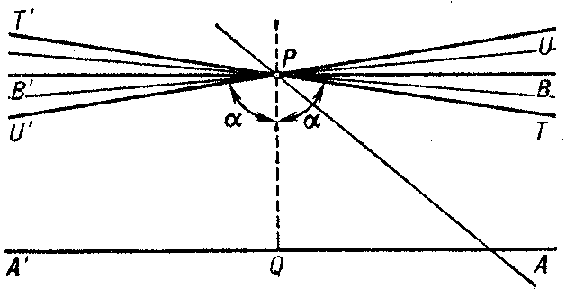
Figure: l060030a

In Lobachevskii geometry the axiom of parallelism requires that through a point $ P $( Fig. a) there passes more than one line not intersecting $ A ^ \prime A $. The non-intersecting lines fill the part of the pencil with vertex $ P $ lying inside a pair of vertically opposite angles $ TPU $ and $ U ^ \prime P T ^ \prime $ situated symmetrically with respect to the perpendicular $ PQ $. The lines that form the sides of the vertically opposite angles separate the intersecting lines from the non-intersecting lines, and they themselves are also non-intersecting. These limiting lines are called the parallels at $ P $ to the line $ A ^ \prime A $ in its two directions: $ T ^ \prime T $ is parallel to $ A ^ \prime A $ in the direction $ A ^ \prime A $, and $ U U ^ \prime $ is parallel to $ A ^ \prime A $ in the direction $ A A ^ \prime $. The remaining non-intersecting lines are called ultraparallels to $ A ^ \prime A $( for details see below).

The angle $ \alpha $, $ 0 < \alpha < \pi /2 $, that a parallel at $ P $ makes with the perpendicular $ PQ $, $ \ang QPT = \ang QPU ^ \prime = \alpha $, is called the angle of parallelism of the interval $ PQ = a $ and is denoted by $ \alpha \equiv \Pi ( a) $. For $ a = 0 $, $ \alpha = \pi /2 $; as $ a $ increases the angle $ \alpha $ decreases, so that for every given $ \alpha $, $ 0 < \alpha < \pi /2 $, there is a definite value of $ a $. This dependence is called the Lobachevskii function:

$$ \Pi ( a) = 2 \mathop{\rm arc} \mathop{\rm tan} ( e ^ {- a / k } ), $$

where $ k $ is a constant that determines the fixed scale of measurement. It is called the radius of curvature of the Lobachevskii space.

Euclidean geometry can be obtained as a limiting case of Lobachevskii geometry when the two parallels passing through $ P $ merge into one, that is, when the set of all lines passing through $ P $ and not intersecting the given line $ A ^ \prime A $ reduce to a unique line. Then the angle $ \alpha = \pi /2 $ for any $ a $. This condition is equivalent to the requirement that $ k = \infty $. In small regions of space, that is, when the linear dimensions of figures are infinitesimal with respect to $ k $, all relations of Lobachevskii geometry are approximated by relations of the Euclidean geometry obtained in the limit.

Two distinct lines of the plane form a pair of one of three types.

Intersecting lines. The distance from points of one line to the other line increases without limit as the distance from the intersection of the lines increases. If the lines are not perpendicular, then each is projected orthogonally on the other into an open interval of finite size.

Parallel lines. Coplanar non-intersecting lines that have no common perpendicular. In Fig. a, $ P T \| Q A $ and $ P U ^ \prime \| QA ^ \prime $, in $ P $, with angle of parallelism $ \alpha $. Parallelism is transitive (if $ a \| b $ and $ b \| c $ in one direction, then $ a \| c $ in the corresponding direction). In the direction of parallelism parallels approach each other without limit (in the sense of the distance from a moving point of one line to the other line). The orthogonal projection of one line on the other is an open half-line.

Ultraparallels. They have one common perpendicular, the length of which gives the shortest distance. On both sides of the perpendicular the lines diverge without limit. Each line projects onto the other in an open interval of finite length.

To the three types of lines there correspond in the plane three types of pencils of lines, each of which covers the whole plane: a pencil of the first kind — the set of all lines passing through one point (the centre of the pencil); a pencil of the second kind — the set of all lines perpendicular to one line (the base of the pencil); and a pencil of the third kind — the set of all lines parallel to one line in a given direction, including this line.

The orthogonal trajectories of the lines of these pencils form analogues of circles of the Euclidean plane: a circle in the proper sense; an equi-distant, or curve of equal distances (if one does not consider the base), which is concave on the side of the base; or a limiting curve, or horocycle, which can be regarded as a circle with its centre at infinity. Horocycles are congruent. They are not compact and are concave on the side of parallelism. Two horocycles generated by the same pencil are concentric (they cut off equal intervals on the lines of the pencil). The ratio of the lengths of concentric arcs included between two lines of the pencil decreases on the side of parallelism like an exponential function of the distance $ x $ between the arcs:

$$ \frac{s ^ \prime }{s} = e ^ {- x / k } . $$

Each of the analogues of a circle can slide on itself, generating three types of one-parameter motions of the plane: rotation about a proper centre; translation (one trajectory is the base, and the others are equi-distants); and parallel displacement (all the trajectories are horocycles).

Rotation of the analogues of circles about a line of the generating pencil leads to analogues of the sphere: a proper sphere, a surface of equal distances and a horosphere, or limiting surface.

On a sphere the geometry of great circles is ordinary spherical geometry; on a surface of equal distances it is the geometry of equi-distants, which is Lobachevskii planimetry, but with a larger value of $ k $; and on a horosphere it is the Euclidean geometry of horocycles.

The connection between lengths of arcs and chords of horocycles and Euclidean trigonometric relations on horospheres make it possible to derive trigonometric relations in the plane, that is, trigonometric formulas for rectilinear triangles. For example, the formula for the area $ \sigma $ of a triangle is:

$$ \sigma = k ^ {2} ( \pi - A - B - C ) ; $$

for the perimeter of a circle the formula is:

$$ l = 2 \pi k \sinh \frac{r}{k} . $$

The trigonometric formulas of Lobachevskii geometry can be obtained from the formulas of spherical geometry by replacing the radius $ R $ by the imaginary number $ ki $.

The proof of the consistency of Lobachevskii geometry is carried out by constructing an interpretation (a model). The first such interpretation was the Beltrami interpretation, which establishes that in Euclidean space the intrinsic geometry of a surface of constant negative Gaussian curvature coincides locally with Lobachevskii geometry (the role of straight lines is played by the geodesic curves of the surface). A surface of this type is called a pseudo-sphere.

Another interpretation of Beltrami consists of a geodesic mapping of a surface of constant negative curvature into the interior of a disc.

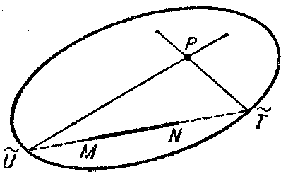
Figure: l060030b

However, the Beltrami interpretations model only part of the Lobachevskii plane. The first interpretation of the whole Lobachevskii plane was the Klein interpretation, in which Cayley's projective metric was used. In this interpretation (Fig. b) the straight lines of Lobachevskii space are realized by chords of the absolute (without the end-points), and perpendicular lines are realized by conjugate chords. Distances and angles are expressed by means of the cross ratios (cf. Cross ratio) of quadruples of points (the end-points $ M $, $ N $ of an interval and the end-points $ \widetilde{U} $, $ \widetilde{T} $ of the chord on which the interval lies) and the corresponding quadruples of lines (the sides of the angle and the (imaginary) tangents to the absolute that pass through the vertex). The parallels through a point $ P $ to the line $ MN $ are realized by the lines $ P \widetilde{T} $ and $ P \widetilde{U} $ that intersect $ MN $ at points on the absolute. The points of the absolute model the "points at infinity" , which are not points of the Lobachevskii plane.

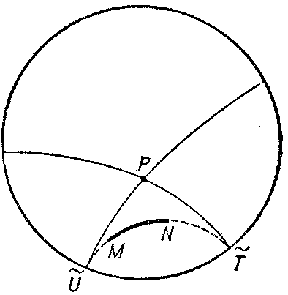
Figure: l060030c

In 1882, H. Poincaré, in constructing a theory of automorphic functions, arrived at two other models, in a disc and on a half-plane (cf. Poincaré model). In the first model (Fig. c) the Lobachevskii plane is realized by the interior of a disc, and lines by the inner parts of arcs of circles that intersect the main disc orthogonally. The metric is introduced by means of cross ratios, and the values of angles on the model are the same as those on the Lobachevskii plane (a conformal model).

The introduction of coordinates makes it possible to obtain different analytical models of the Lobachevskii plane. Poincaré, in 1887, proposed a model of Lobachevskii geometry as the geometry of plane diametral sections of one of the sheets of a two-sheet hyperboloid, which can also be treated as the geometry of a sphere of purely imaginary radius in a pseudo-Euclidean space. These models can be generalized to the case of an $ n $- dimensional space.

Like elliptic geometry, Lobachevskii geometry is the geometry of a Riemannian space of constant curvature.

The origin of the creation of Lobachevskii geometry was the problem of parallels, that is, attempts to prove Euclid's fifth postulate concerning parallels. N.I. Lobachevskii (1826, published in 1829–1830) showed that the assumption of a postulate different from Euclid's postulate makes it possible to construct Lobachevskii geometry, which is more general than Euclidean geometry. Independently of Lobachevskii, J. Bolyai arrived at the same discovery in 1832. Not having obtained the open support of C.F. Gauss, Bolyai did not continue his research.

Gauss worked out the beginnings of the new geometry much earlier, but he did not publish this research, and never spoke openly about these ideas. However, in private correspondence he regarded the work of Bolyai and Lobachevskii highly, but he did not say so openly in print.

Applications of Lobachevskii geometry.

In the first work on his geometry, Lobachevskii, relying on the yearly parallax of stars first measured by the astronomers of the time, showed that if his geometry is realized in physical space, then within the limits of the Solar System the deviations from Euclidean geometry would be several orders smaller than possible measuring errors. Thus, the first application of Lobachevskii geometry was a justification of the practical accuracy of Euclidean geometry.

Lobachevskii applied his geometry to mathematical analysis. Going over from one coordinate system to another in his space, he found the values of about 200 distinct definite integrals. Other mathematical applications were found by Poincaré (1882), who successfully applied Lobachevskii geometry to the development of the theory of automorphic functions.

The significance of Lobachevskii geometry for cosmology was first explained by A.A. Friedman. In 1922 he found a solution of the Einstein equations which implied that the universe expands in the course of time. This conclusion was subsequently confirmed by observations of E. Hubble (1929), who discovered the scattering of distant nebuli. The metric found by Friedman gives, for a fixed time, the Lobachevskii space. The velocity space of the special theory of relativity is a Lobachevskii space.

Lobachevskii geometry has been used successfully in the study of collisions of elementary particles and in the development of other questions of nuclear research.

Visual perception of nearby regions of space by man provides the effect of inverse perspective, which is explained by the fact that the geometry of these regions of perspective space are close to Lobachevskii geometry with radius of curvature of about 15 metres.

The creation of Lobachevskii geometry was an important step in the development of studies on the possible properties of space. It also had special significance for the foundations of mathematics, since the principles of the modern axiomatic method were worked out to a significant extent thanks to the appearance of Lobachevskii geometry.

References

[1]	N.I. Lobachevskii, "Zwei geometrische Abhandlungen" , Teubner (1898) (Translated from Russian)
[2]	J. Bolyai, "Appendix. Scientiam spatii absolute veram exhibens" , Tentamen , 1 , M. Vásárhelyini Die (1833)
[3]	A.D. Aleksandrov, "Abstract spaces" , Mathematics, its content, methods and meaning , 3 , Amer. Math. Soc. (1962) (Translated from Russian)
[4]	I.P. Egorov, "Introduction to non-Euclidean geometries" , Penze (1972) (In Russian)
[5]	N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian)
[6]	V.F. Kagan, "Foundations of geometry" , 1 , Moscow-Leningrad (1949) (In Russian)
[7]	B.L. Laptev, "Nikolai Ivanovich Lobachevskii" , Kazan' (1976) (In Russian)
[8]	A.P. Norden, "Elementare Einführung in die Lobatschewskische Geometrie" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian)
[9]	Yu.Yu. Nut, "Lobachevskii geometry in an analytic setting" , Moscow (1961) (In Russian)
[10]	B.V. Raushenbakh, "Spatial constructions in old Russian paintings" , Moscow (1975) (In Russian)
[11]	B.A. Rozenfel'd, "Non-Euclidean spaces" , Moscow (1969) (In Russian)
[12]	P.A. Shirokov, "A sketch of the fundamentals of Lobachevskian geometry" , Noordhoff (1964) (Translated from Russian)

Comments

Lobachevskii geometry is also called hyperbolic geometry. Just as in spherical geometry it is natural to use a sphere of radius $ R = 1 $, in Lobachevskii geometry one usually assumes $ k = 1 $, thereby simplifying somewhat the formulas. (E.g. $ \Pi ( a) = 2 { \mathop{\rm arc} \mathop{\rm tan} } e ^ {-} a $, $ \sigma = \pi - A - B - C $, $ l = 2 \pi \sinh r $.)

Beltrami could have anticipated F. Klein, by combining his two interpretations.

For the introduction in Poincaré's first model (Fig. c) of a metric avoiding cross ratios see [a2].

Concerning some history see also [a9]. This reference also includes translations of a paper by Lobachevskii and of the $ Appendix $[2] by Bolyai.

References

[a1]	H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 224–240
[a2]	H.S.M. Coxeter, "Parallel lines" Canad. Math. Bull. , 21 (1978) pp. 385–397
[a3]	H.S.M. Coxeter, "The non-Euclidean symmetry of Escher's picture "Circle Limit III" " Leonardo , 12 (1979) pp. 19–25; 32
[a4]	H.S.M. Coxeter, "Angles and arcs in the hyperbolic plane" Math. Chronicle (New Zealand) , 9 (1980) pp. 7–33
[a5]	M. Berger, "Geometry" , 1–2 , Springer (1987) (Translated from French)
[a6]	M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974)
[a7]	D.M.Y. Sommerville, "Bibliography of non-Euclidean geometry" , Chelsea, reprint (1970)
[a8]	H.S.M. Coxeter, "Introduction to geometry" , Wiley (1961) pp. 11; 258
[a9]	R. Bonola, "Non-Euclidean geometry" , Dover, reprint (1955) (Translated from Italian)