Webs, geometry of
The part of differential geometry that studies families of curves and surfaces — so-called webs (flat, spatial or multi-dimensional).
A flat $p$-web (planar $p$-web) is a domain in the plane in which one is given $p$ (usually $p\geq3$) families of sufficiently smooth curves with the properties: 1) exactly one curve from each family passes through each point of the domain; and 2) curves from distinct families have at most one common point. Example: the three families of straight lines parallel to the sides of an equilateral triangle form a $3$-web (a regular web).
The fundamental object of study in the geometry of webs are the properties that are invariant under differential-topological transformations. Webs are called equivalent if they are (locally or globally) diffeomorphic. For $p=2$ a web is diffeomorphic to the web formed by two collections of parallel lines (such webs are called nets, cf. Net (in differential geometry)). For $p=3$ a web is, in general, neither diffeomorphic to three collections of parallel lines (that is, is not a hexagonal web), nor to three collections of straight lines at all (that is, it is not a rectifiable web). The condition of hexagonality for webs in geometric form is a closure condition. The condition of rectifiability cannot be described in a visible form; it is studied in connection with problems of nomography.
A spatial curvilinear web consists of $p$ families of curves in space with the condition that through each point in the domain there passes one curve of each family. These webs are not all diffeomorphic, even for $p=2$. Of special interest are quadrilateral webs, whose lines form nets on the surfaces of a one-parameter family.
A spatial surface web consists of $p$ families of surfaces, with the condition that through each point there passes one surface from each family, and that three surfaces from distinct families have at most a single point in common. For such webs, and their multi-dimensional analogues, one can also introduce the notion of rectifiability (that is, of diffeomorphism to a web formed by families of planes (hyperplanes)). A $4$-web is called an octahedral web if the $3$-web formed by the intersections of any three families with a surface from the fourth is hexagonal.
Multi-dimensional webs consist of $p$ families of submanifolds in a multi-dimensional space. For example, three families of $r$-dimensional submanifolds of a $2r$-dimensional space form a $3$-web if one submanifold from each family passes through each point, and if submanifolds from two distinct families have at most one common point.
The geometry of webs considers also projective-differential, affine-differential and other properties of webs in connection with the geometry of the manifold carrying the web. One considers webs made up of geodesic lines (cf. Geodesic line), lines connected with the Darboux tensor, etc.
The definition of a curve of the third family in terms of the curves of the other two (in the case of a flat $3$-web) can be considered as an algebraic operation of quasi-group type. Hence, the notion of an abstract web, or algebraic net, arose (cf. Quasi-group).
References
| [1] | W. Blaschke, "Einführung in die Geometrie der Waben" , Birkhäuser (1955) |
| [2] | V.D. Belousov, V.V. Ryzhkov, "Geometry of webs" J. Soviet Math. , 2 : 3 (1974) pp. 331–348 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 10 (1972) pp. 159–188 |
| [3] | V.I. Shulikovskii, "Classical differential geometry in a tensor setting" , Moscow (1963) (In Russian) |
Comments
References
| [a1] | W. Blaschke, G. Bol, "Geometrie der Gewebe" , Springer (1938) |
| [a2] | V.V. Goldberg, "Theory of multicodimensional (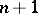 )-webs" , Kluwer (1988) )-webs" , Kluwer (1988) |
| [a3] | S.S. Chern, P.A. Griffiths, "Abel's theorem and webs" Jahresber. Deutsch. Math. Verein. , 80 (1978) pp. 13–110 ((Addenda et corrigenda: 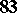 (1981), pp. 78–83.)) (1981), pp. 78–83.)) |
| [a4] | S.S. Chern, "Web geometry" Bull. Amer. Math. Soc. , 6 (1982) pp. 1–8 |
| [a5] | M.A. Akivis, A.M. Shelekhov, "Geometry and algebra of multidimensional three webs" , Kluwer (1992) (Translated from Russian) |
Webs, geometry of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Webs,_geometry_of&oldid=31692