Partially specified matrices, completion of
A partially specified $ ( p \times q ) $-matrix is a $ ( p \times q ) $-array of complex numbers (or, more generally, of elements over an arbitrary field) in which certain entries are given and the other entries are not specified. The latter are often denoted by question marks and may be viewed as free variables. The set of pairs $ ( i,j ) $
for which the $ ( i,j ) $th entry is given is called the pattern. For example,
$$ \left ( \begin{array}{ccc} 1 & ? & 2 \\ ? & 0 & 5 \\ 3 & ? & ? \\ \end{array} \right ) $$
is a partially specified $ ( 3 \times 3 ) $-matrix with pattern $ {\mathcal P} = \{ ( 1,1 ) , ( 1,3 ) , ( 2,2 ) , ( 2,3 ) , ( 3,1 ) \} $. Important patterns are band patterns, when $ {\mathcal P} = \{ {( i,j ) } : {| {i - j } | \leq m } \} $ for some $ m $, triangular patterns, when the set of given entries is upper or lower triangular, and rectangular patterns, when $ {\mathcal P} $ has the form
$$ {\mathcal P} = \left \{ {( i,j ) } : {i \in \{ i _ {1} \dots i _ {k} \} , j \in \{ j _ {1} \dots j _ {m} \} } \right \} $$
and the given entries form a positioned submatrix. The block versions of band and triangular patterns are also of interest.
A $ ( p \times q ) $-matrix $ A $ is said to be a completion of a partially specified matrix $ A _ {\mathcal P} $ with pattern $ {\mathcal P} $ if for each $ ( i,j ) \in {\mathcal P} $ the $ ( i,j ) $th entry of $ A $ coincides with the $ ( i,j ) $th entry of $ A _ {\mathcal P} $. The analysis of completions satisfying additional metric or spectral constraints is a relatively new direction in linear algebra, with many different aspects depending on the given pattern and the type of constraint imposed. In general, one looks for a description of all possible completions of a desired type, and for algorithms for the construction of particular ones. Completion problems arise in a variety of applications, such as statistics (e.g., entropy methods for missing data), chemistry (the molecular conformation problem), systems theory, discrete optimization (relaxation methods), data compression, etc., as well as in operator theory and within matrix theory (e.g., determinantal inequalities). Of particular interest are the following problems.
Positive-definite completion problem.
This problem asks one to find completions of a partially specified matrix that are positive definite. For band patterns the problem is also known as the covariance extension problem and may be viewed as a non-stationary version of the Carathéodory–Toeplitz extension problem. Furthermore, in this case the solution of the problem may be described entirely in terms of the fully specified principal submatrices, the set of all solutions can be parametrized by a fractional-linear mapping of which the coefficients can be constructed explicitly in terms of the given entries, and there exists a unique solution of maximal determinant which has the additional property that the entries of its inverse are zero outside the band. These results, which also extend to block-banded operator matrices and integral operators, can be proved by different methods, among others the Schur parametrization approach (see [a6]) and the band method (see [a12], comments to Part IX, and [a23], Part A). For non-band patterns similar results (except for the description of all solutions) hold if the graph associated with the pattern is chordal (see [a16]). For non-chordal patterns the situation is much more complex and only partial results are known (see [a21] and [a4]). The positive-definite completion problem is closely related to the contractive completion problem. The latter problem, which may be seen as the non-stationary matrix version of the Nehari extension problem, asks one to complete a given triangular array to a full matrix of which the operator norm does not exceed a given bound. The $ ( 2 \times 2 ) $ operator matrix case is of special interest (see [a8], notes and comments to Chapt. IV). More recent developments include linearly constrained contractive completion problems (also known as the strong Parrott problem; see [a9], [a2]) and completions satisfying bounds for different norms simultaneously (see [a20]).
Eigenvalue completion problem.
This problem concerns the following question: To what extent does a partially specified matrix $ A _ {\mathcal P} $ determine the eigenvalues and their multiplicities of its completions? In other words, this problem asks one to describe all possible eigenvalues and their multiplicities of the matrices which one obtains by filling in the unspecified entries of $ A _ {\mathcal P} $. It contains as a special case the pole assignment problem from mathematical system theory. Associated with the eigenvalue completion problem is a classification problem which aims at a simplification of the specified part with the help of admissible similarities (which do not relate specified entries to unspecified ones) and has as its final goal the construction of related canonical forms. For rectangular patterns this classification problem is completely solved, and its solution has been used to solve the eigenvalue completion problem for a number of rectangular patterns, namely for the case when the set of given entries forms a principal submatrix, a full-width submatrix, a full-length submatrix, or an off-diagonal submatrix (see [a13]). These and related results for triangular patterns (such as the solution of the minimal spectral radius problem from [a3]) and further references may be found in [a14]. The latter also includes infinite-dimensional operator versions of these spectral completion problems. The classification problem referred to above is also closely related to the problem of classifying quadruples of subspaces under isomorphism of subspace quadruples, [a10], [a15].
Minimal rank completion problem.
This problem asks one to determine the completions of a partially specified matrix $ A _ {\mathcal P} $ that are of minimal rank. In particular, one is interested in finding the lowest possible rank of a completion of $ A _ {\mathcal P} $ in terms of the given entries, and in conditions that guarantee the uniqueness of this minimal rank completion. For triangular patterns the minimal rank completion problem is solved in [a23], Part B; for this case the problem is closely related to the Kalman partial realization problem in mathematical system theory. For band patterns a formula for the minimal rank of a completion may be found in [a24]. For more general patterns only partial solutions exist [a5]. The problem extends naturally to semi-infinite matrices and to integral operators, [a18], [a19], [a22], and in these infinite-dimensional settings the problem is related to minimal realizations of boundary value systems.
There are many other important completion problems, such as the minimal inertia completion problems (see, e.g., [a11]), completion problems for particular classes of matrices such as distance matrices [a1] and $ M $-matrices [a17], and problems which require the completion to be an invertible matrix of which the inverse (rather than the completion itself) has to satisfy additional constraints (see, e.g., [a7]).
References
| [a1] | M. Bakonyi, C.R. Johnson, "The Euclidean distance matrix completion problem" SIAM J. Matrix Anal. Appl. , 16 (1995) pp. 646–654 |
| [a2] | M. Bakonyi, H.J. Woerdeman, "The central method for positive semi-definite, contractive and strong Parrott type completion problems" , Operator Theory: Advances and Applications , 59 , Birkhäuser (1992) pp. 78–95 |
| [a3] | J.A. Ball, I. Gohberg, L. Rodman, T. Shalom, "On the eigenvalues of matrices with given upper triangular part" Integral Eq. Operator Th. , 13 (1990) pp. 488–497 |
| [a4] | W.W. Barrett, C.R. Johnson, R. Loewy, "The real positive definite completion problem for nonchordal graphs" , Memoirs , 122 , Amer. Math. Soc. (1996) |
| [a5] | N. Cohen, C.R. Johnson, L. Rodman H.J. Woerdeman, "Ranks of completions of partial matrices" H. Dym (ed.) S. Goldberg (ed.) M.A. Kaashoek (ed.) P. Lancaster (ed.) , The Gohberg Anniversary Collection, Vol. II , Operator Theory: Advances and Applications , 41 , Birkhäuser (1989) |
| [a6] | T. Constantinescu, "Schur parameters, factorization and dilation problems" , Operator Theory: Advances and Applications , 82 , Birkhäuser (1996) |
| [a7] | L. Elsner, C. He, V. Mehrmann, "Minimization of the norm, the norm of the inverse and the condition number of a matrix by completion" Numerical Linear Alg. Appl. , 2 : 2 (1995) pp. 155–171 |
| [a8] | C. Foias, A.E. Frazho, "The commutant lifting approach to interpolation problems" , Operator Theory: Advances and Applications , 44 , Birkhäuser (1990) |
| [a9] | C. Foias, A. Tannenbaum, "A strong Parrott theorem" Proc. Amer. Math. Soc. , 106 (1989) pp. 777–784 |
| [a10] | I.M. Gel'fand, V.A. Ponomarev, "Problems of linear algebra and classification of subspaces in a finite-dimensional vector space" , Colloq. Math. Soc. J. Bolyai (Hilbert Space Operators, Tihany) , 5 , North-Holland (1970) pp. 163–237 |
| [a11] | A. Gheondea, "One-step completions of Hermitian partial matrices with minimal negative signature" Linear Alg. & Its Appl. , 173 (1992) pp. 99–114 |
| [a12] | I. Gohberg, S. Goldberg, M.A. Kaashoek, "Classes of linear operators II" , Operator Theory: Advances and Applications , 63 , Birkhäuser (1993) |
| [a13] | I. Gohberg, M.A. Kaashoek, F. van Schagen, "Eigenvalues of completions of submatrices" Linear Multilinear Algebra , 25 (1989) pp. 55–70 |
| [a14] | I. Gohberg, M.A. Kaashoek, F. van Schagen, "Partially specified matrices: similarity, completions and applications" , Operator Theory: Advances and Applications , 79 , Birkhäuser (1995) |
| [a15] | I. Gohberg, M.A. Kaashoek, F. van Schagen, "Operator blocks and quadruples of subspaces: classification and the eigenvalue completion problem" Vrije Universiteit, Amsterdam, Rapportnr. WS-455 (1996) (Also: Lin. Algebra and Its Appl. (to appear)) |
| [a16] | J. Grone, C.R. Johnson, E.M. de Sá, H. Wolkowitz, "Positive definite completions of partial hermitian matrices" Linear Alg. & Its Appl. , 58 (1984) pp. 109–124 |
| [a17] | C.R. Johnson, R. Smith, "The completion problem for 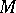 -matrices and inverse -matrices and inverse 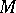 -matrices" Linear Alg. & Its Appl. , 241/3 (1996) pp. 655–667 -matrices" Linear Alg. & Its Appl. , 241/3 (1996) pp. 655–667 |
| [a18] | M.A. Kaashoek, H.J. Woerdeman, "Unique minimal rank extensions of triangular operators" J. Math. Anal. Appl. , 131 (1988) pp. 501–516 |
| [a19] | M.A. Kaashoek, H.J. Woerdeman, "Minimal lower separable representations: construction and characterization" H. Dym (ed.) S. Goldberg (ed.) M.A. Kaashoek (ed.) P. Lancaster (ed.) , The Gohberg Anniversary Collection, Vol II , Operator Theory: Advances and Applications , 41 , Birkhäuser (1989) |
| [a20] | V.G. Kaftal, D.R. Larson, G. Weiss, "Quasitriangular subalgebras of semifinite von Neumann algebras are closed" J. Funct. Anal. , 107 (1992) pp. 387–401 |
| [a21] | V.I. Paulsen, S.C. Power, R.R. Smith, "Schur products and matrix completions" J. Funct. Anal. , 85 (1989) pp. 151–178 |
| [a22] | G. Peeters, "Construction and classification of minimal representations of semi- separable kernels" J. Math. Anal. Appl. , 137 (1989) pp. 264–287 |
| [a23] | H.J. Woerdeman, "Matrix and operator extensions" , CWI Tracts , 68 , CWI , Amsterdam (1989) |
| [a24] | H.J. Woerdeman, "Minimal rank completions of partial banded matrices" Linear Multilinear Algebra , 36 (1993) pp. 59–68 |
Partially specified matrices, completion of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Partially_specified_matrices,_completion_of&oldid=52134