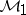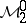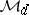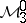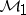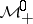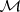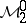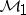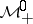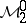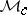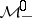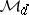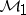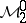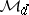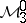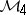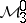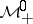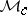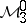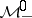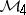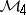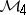Band method
A framework for solving various positive-definite and strictly contractive extension problems and various interpolation problems from a unified abstract point of view. This method applies to algebras with band structure. An algebra 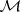 with an identity
with an identity  and an involution
and an involution  is called an algebra with band structure if
is called an algebra with band structure if 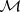 admits a direct sum decomposition
admits a direct sum decomposition
 | (a1) |
where all the summands are subspaces of 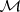 such that the following conditions are satisfied:
such that the following conditions are satisfied:
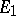 )
) 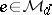 ;
;
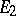 )
) 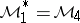 ,
, 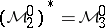 ,
, 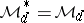 ;
;
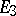 ) the following multiplication table holds:
) the following multiplication table holds:
<tbody> </tbody>
|
where
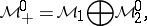 |
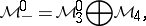 |
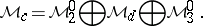 |
The space 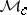 is called the band of
is called the band of 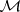 , and any element in
, and any element in 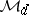 is called a diagonal. Also, let
is called a diagonal. Also, let
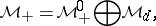 |
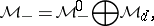 |
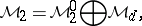 |
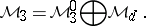 |
The natural projections associated with the decomposition (a1) are denoted by 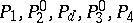 , respectively.
, respectively.
An example of an algebra with band structure is the Wiener algebra 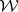 of all complex-valued functions
of all complex-valued functions 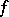 on the unit circle
on the unit circle 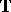 that have absolutely convergent Fourier series expansions
that have absolutely convergent Fourier series expansions
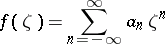 |
with
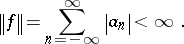 |
The involution on 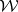 is complex conjugation. Let
is complex conjugation. Let 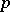 be a fixed positive integer. A band structure on
be a fixed positive integer. A band structure on  is obtained by letting the summands in (a1) be defined by
is obtained by letting the summands in (a1) be defined by
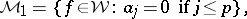 |
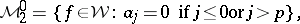 |
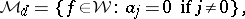 |
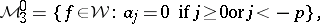 |
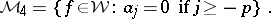 |
An element 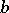 in an algebra
in an algebra 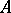 with involution
with involution  and unit
and unit  is called positive definite in
is called positive definite in 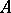 if
if 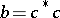 for some invertible
for some invertible 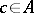 . Such an element in an algebra
. Such an element in an algebra 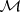 with band structure is said to admit a right (respectively, left) spectral factorization if
with band structure is said to admit a right (respectively, left) spectral factorization if  and
and 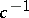 can be taken in
can be taken in 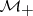 (respectively,
(respectively, 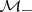 ).
).
Hereafter, 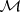 is assumed to be a
is assumed to be a  -subalgebra of a unital
-subalgebra of a unital  -algebra
-algebra 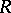 , with the unit of
, with the unit of 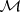 equal to the unit of
equal to the unit of 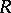 . Let
. Let 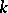 be an element in the band
be an element in the band 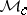 . An
. An 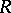 -positive extension of
-positive extension of 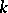 is an element
is an element 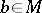 that is positive definite in
that is positive definite in 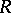 such that
such that
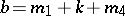 |
for certain elements 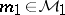 and
and 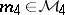 . A band extension of
. A band extension of 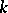 is an
is an 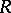 -positive extension
-positive extension 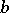 of
of 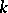 such that
such that  . The main problems are to determine conditions under which a band extension of
. The main problems are to determine conditions under which a band extension of 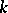 exists, to find the band extension when it exists, and to describe all
exists, to find the band extension when it exists, and to describe all 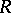 -positive extensions of
-positive extensions of 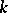 when
when 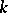 has a band extension. The following two statements provide solutions of these problems.
has a band extension. The following two statements provide solutions of these problems.
I) Let 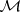 be an algebra with band structure (a1), and let
be an algebra with band structure (a1), and let 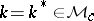 . Then
. Then 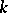 has a band extension
has a band extension 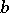 with a right spectral factorization relative to (a1) if and only if the equation
with a right spectral factorization relative to (a1) if and only if the equation
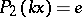 | (a2) |
has a solution  with the following properties:
with the following properties:
i) 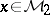 ;
;
ii)  is invertible and
is invertible and 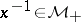 ;
;
iii) 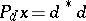 for some
for some 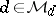 which is invertible in
which is invertible in 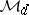 . Furthermore, in this case such an element
. Furthermore, in this case such an element 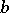 is obtained by taking
is obtained by taking
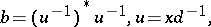 |
where  is any solution of (a2) satisfying i)–iii).
is any solution of (a2) satisfying i)–iii).
To describe all 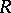 -positive extensions of
-positive extensions of 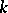 , it will be additionally assumed that the following axiom holds:
, it will be additionally assumed that the following axiom holds:
Axiom 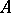 : If
: If 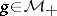 and
and  , then
, then 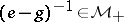 .
.
This axiom holds if 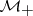 is closed in
is closed in 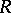 .
.
II) Let 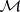 be an algebra with band structure (a1) in a unital
be an algebra with band structure (a1) in a unital 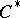 -algebra
-algebra 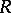 , and assume that axiom
, and assume that axiom 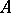 holds. Let
holds. Let 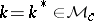 , and suppose that
, and suppose that 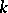 has a band extension
has a band extension 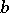 which admits a right and left spectral factorization relative to (a1):
which admits a right and left spectral factorization relative to (a1):
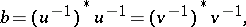 |
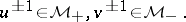 |
Then each 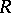 -positive extension of
-positive extension of 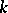 is of the form
is of the form
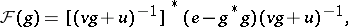 | (a3) |
where the free parameter 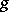 is an arbitrary element in
is an arbitrary element in 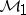 such that
such that 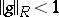 . Moreover, the mapping
. Moreover, the mapping 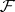 provides a one-to-one correspondence between all such
provides a one-to-one correspondence between all such 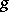 and all
and all 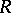 -positive extensions of
-positive extensions of 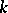 .
.
In the above statement, 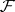 may be replaced by
may be replaced by
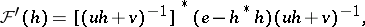 |
where now the free parameter 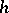 is an arbitrary element of
is an arbitrary element of 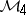 such that
such that 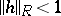 .
.
The right-hand side of (a3) yields a positive extension (i.e., an extension which is positive definite in 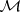 ) if and only if the free parameter
) if and only if the free parameter 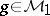 is such that
is such that 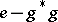 is positive definite in
is positive definite in 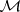 .
.
An alternative characterization of the band extension is provided by an abstract maximum entropy principle. For this it is necessary to assume two additional axioms. An element 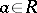 is positive semi-definite in
is positive semi-definite in 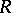 if
if  for some
for some 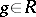 .
.
Axiom 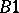 : If
: If 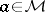 is positive semi-definite in
is positive semi-definite in 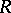 , then
, then 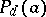 is positive semi-definite in
is positive semi-definite in 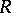 .
.
Axiom 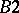 : If
: If 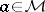 is positive semi-definite in
is positive semi-definite in 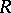 and
and 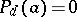 , then
, then 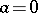 .
.
Any element 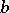 of
of 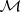 with a right spectral factorization can be factored uniquely in the form
with a right spectral factorization can be factored uniquely in the form
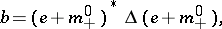 |
where 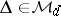 and
and 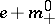 is invertible with
is invertible with 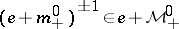 . The element
. The element 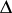 is called the right multiplicative diagonal of
is called the right multiplicative diagonal of 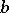 and is denoted by
and is denoted by 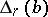 . The maximum entropy principle states that if a self-adjoint element
. The maximum entropy principle states that if a self-adjoint element 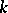 in
in 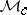 (cf. also Self-adjoint operator) has a band extension
(cf. also Self-adjoint operator) has a band extension 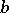 with a right spectral factorization, then for any
with a right spectral factorization, then for any 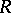 -positive extension
-positive extension  of
of 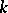 having a right spectral factorization,
having a right spectral factorization,
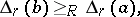 |
with equality only if 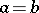 .
.
Solution of the Carathéodory–Toeplitz extension problem.
There are many applications of these results to various algebras of functions, matrix-valued functions, and matrices. When applied to the Wiener algebra 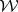 with the band structure described above, they yield a description of the solutions of the classical Carathéodory–Toeplitz extension problem.
with the band structure described above, they yield a description of the solutions of the classical Carathéodory–Toeplitz extension problem.
Given a trigonometric polynomial
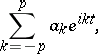 | (a4) |
one looks for a function 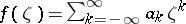 in
in 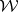 with the property that
with the property that 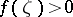 for every
for every 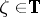 . The following statement gives the solution.
. The following statement gives the solution.
The Carathéodory–Toeplitz extension problem for the trigonometric polynomial (a4) is solvable if and only if the matrix
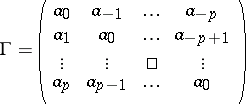 |
is positive definite. In that case there exists a unique solution 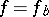 with the additional property that the
with the additional property that the 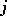 th Fourier coefficient of
th Fourier coefficient of 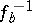 is equal to
is equal to  for
for 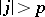 .
.
To obtain 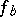 , let
, let
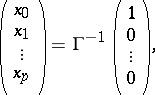 |
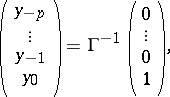 |
and define
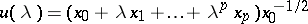 |
and
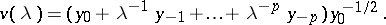 |
Then  for
for 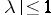 and
and 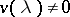 for
for 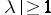 and
and
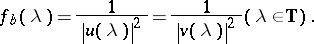 |
Furthermore, every solution 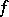 of the Carathéodory–Toeplitz problem is of the form
of the Carathéodory–Toeplitz problem is of the form
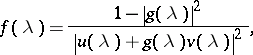 | (a5) |
where 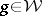 is an arbitrary function with
is an arbitrary function with 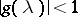 for
for 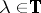 and with the
and with the 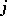 th Fourier coefficient of
th Fourier coefficient of 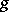 equal to
equal to  for
for 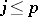 . Moreover, (a5) gives a one-to-one correspondence between all such
. Moreover, (a5) gives a one-to-one correspondence between all such 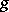 and all solutions
and all solutions 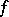 . Additionally, the band solution
. Additionally, the band solution 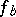 is the unique solution
is the unique solution 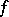 that maximizes the entropy integral
that maximizes the entropy integral
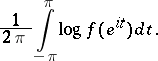 |
This solution is called the maximum entropy solution.
Strictly contractive extension problems, such as the Nehari extension problem of complex analysis, can be reduced to band extension problems. Further details can be found in [a1], Chapts. XXXIV–XXXV.
The band method has its origin in the papers [a2], [a3], and has been developed further in [a4], [a5], [a6]. Additional references can also be found in [a1].
References
| [a1] | I. Gohberg, S. Goldberg, M.A. Kaashoek, "Classes of linear operators II" , Operator Theory: Advances and Applications , 63 , Birkhäuser (1993) |
| [a2] | H. Dym, I. Gohberg, "Extensions of kernels of Fredholm operators" J. Anal. Math. , 42 (1982/3) pp. 51–97 |
| [a3] | H. Dym, I. Gohberg, "A new class of contractive interpolants and maximum entropy principles" , Operator Theory: Advances and Applications , 29 , Birkhäuser (1988) pp. 117–150 |
| [a4] | I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "The band method for positive and conntractive extension problems" J. Operator Th. , 22 (1989) pp. 109–155 |
| [a5] | I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "The band method for positive and conntractive extension problems: An alternative version and new applications" Integral Eq. Operator Th. , 12 (1989) pp. 343–382 |
| [a6] | I. Gohberg, M.A. Kaashoek, H.J. Woerdeman, "A maximum entropy principle in the general framework of the band method" J. Funct. Anal. , 95 (1991) pp. 231–254 |
Band method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Band_method&oldid=42683