Grammar, context-sensitive
grammar of direct components, context grammar, grammar of components
A special case of a generative grammar $ \Gamma = \langle V, W, I, R \rangle $( cf. Grammar, generative) each rule of which has the form $ \xi _ {1} A \xi _ {2} \rightarrow \xi _ {1} \theta \xi _ {2} $, where $ \xi _ {1} , \xi _ {2} , \theta $ are strings in the alphabet $ V \cup W $, $ A \in W $ and $ \theta $ is non-empty. Each step of a derivation in a context-sensitive grammar consists in replacing an occurrence of the symbol $ A $ by an occurrence of the string $ \theta $, the possibility of such a replacement being enabled by the presence of the "context" $ \xi _ {1} , \xi _ {2} $. The occurrences of symbols in $ \theta $ can then also be replaced, etc. Thus, the occurrence of a symbol is "expanded" into some segment of the string produced as a result of the derivation. This makes it possible to represent a derivation in a context-sensitive grammar with the aid of a tree (a derivation tree). E.g. if the rules of the grammar are $ I \rightarrow AAB $, $ AB \rightarrow DBB $, $ aBB \rightarrow abB $, $ A \rightarrow a $, $ D \rightarrow a $, $ B \rightarrow C $, $ C \rightarrow c $( where $ a, b, c, d $ are the terminal symbols; $ I, A, B, C, D $ are non-terminal symbols, and $ I $ is the initial symbol), then the derivation $ ( I , AAB , aAB , aDBB , aaBB , aabB , aabC , aabc ) $ has the tree reproduced in the figure.
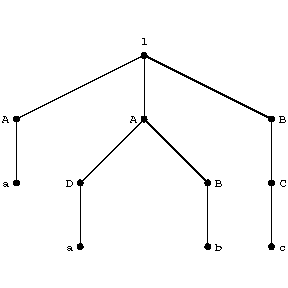
Figure: g044790a
The set of all segments of the last string of the derivation, obtained by "expanding" the non-terminal symbols — or, in other words, "originating" from (non-terminal) vertices of the tree — forms a system of components of this string after all the one-point segments have been added (cf. Syntactic structure); hence also the name "grammar of components" . If all the one-point segments are also obtained by the replacement of the occurrences of non-terminal symbols, it is possible to obtain a marked system of components by assigning to each component, as marks, the non-terminal symbols from the occurrences of which it "originates" . Thus, in the example above, the following marked system of components is obtained:
$$ ((a) A ((a) D (b) B) A (c) B, C) I $$
(here the boundaries of the components are shown by parentheses, while the marks follow the right parenthesis). The assignment of the components to the strings of marked systems forms the foundation of the linguistic applications of context-sensitive grammars. Thus, a grammar whose rules include (among others)
$$ \mathop{\rm STAT} \rightarrow N _ {\textrm{ male } , \textrm{ no } , \textrm{ case } } \widetilde{V} {} ^ {3 } ,\ \ \widetilde{V} {} ^ {3 } \rightarrow V ^ {t3} N _ { \mathop{\rm fem} , \textrm{ no } , \mathop{\rm acc} } , $$
$$ N _ {\textrm{ male } , \textrm{ no } , \textrm{ case } } \rightarrow \ { 'ellipse' },\ \ N _ { \mathop{\rm fem} , \textrm{ no } , \mathop{\rm acc} } \rightarrow \ { 'parabola' }, $$
$$ V ^ {t3} \rightarrow { 'intersects' } $$
where $ \mathop{\rm STAT} $, $ N _ {zyz} $, $ \widetilde{V} {} ^ {3 } $, $ V ^ {t3} $ are non-terminal symbols, standing, respectively, for "statement" , "nouns of gender x, number y and case z" , "verb group in the third person" , and "transitive verb in the third person" , while the symbol $ \mathop{\rm STAT} $ is the initial symbol, assigns to the statement "Ellipse intersects parabola" the marked system of components
$$ ((Ellipse) \ \ N _ {\textrm{ male } , \textrm{ no } , \textrm{ case } } \ ((intersects) V ^ {t3} (parabola) S _ { \mathop{\rm fem} , \textrm{ no } , \textrm{ acc } } ) \widetilde{V} {} ^ {3} ) \textrm{ STAT } $$
The mathematical significance of context-sensitive grammars stems, first and foremost, from the fact that the languages they generate (the so-called context-sensitive languages) are a simple subclass of the class of primitive recursive sets: the class of context-sensitive languages coincides with the class of languages recognized by linearly-bounded Turing machines with one tape and one head (cf. Turing machine). "Concrete" numerical sets often turn out to be context-sensitive languages when ordinary methods of coding natural numbers are applied (these include, for example, the set of perfect squares, the set of prime numbers, the set of decimal approximations of the number $ \sqrt 2 $, etc.).
For each context-sensitive grammar it is possible to construct an equivalent left-context (or right-context) sensitive grammar, i.e. a context-sensitive grammar all rules of which have the form $ \xi A \rightarrow \xi \theta $( or, correspondingly, $ A \xi \rightarrow \theta \xi $). Any context-sensitive grammar all rules of which have the form $ x A y \rightarrow x \theta y $, where $ x, y $ are strings in the basic alphabet, is equivalent to a context-free grammar (cf. Grammar, context-free).
The class of context-sensitive languages is closed under union, intersection, concatenation, truncated iterations, and permutations; it is not known if it is closed under complementation.
Complexity of derivation.
The time complexity (number of elementary derivation steps) of a derivation in a context-sensitive grammar is bounded from above by an exponential function. There exist languages generated by a context-sensitive grammar with time complexity of order $ n ^ {2} $, and which are not generated by any context-sensitive grammars with time complexity of a lower order (the language $ \{ {xbx } : {x \in \{ a _ {1} , a _ {2} \} ^ {*} }\} $ serves as an example); examples of higher estimates from below of the time complexity are not known. The space complexity (maximal length intermediate phrase in derivation) of any context-sensitive grammar is clearly $ n $; for any generative grammar whose space complexity is bounded from above by a linear function
$$ f (n) = kn, $$
there exists a context-sensitive grammar equivalent to it. It can be effectively constructed if $ k $ is known.
Algorithmic problems.
If a certain class of languages contains even one context-sensitive language, and if for at least one context-sensitive language $ L _ {0} $ it contains only a finite number of languages "almost equal" to $ L _ {0} $( two languages $ L _ {1} $ and $ L _ {2} $ are "almost equal" if their symmetric difference $ (L _ {1} - L _ {2} ) \cup (L _ {2} - L _ {1} ) $ is finite), then the property of belonging to the given class is not decidable in the class of context-sensitive grammars. In particular, such undecidable properties include being an empty, finite, regular, linear, or context-free language; having an empty or finite complement; and being equal to some (any) fixed context-sensitive language. An example of a property which is decidable in the class of context-sensitive grammars is: a given string belongs to the generated language.
See also Grammar, context-free.
Comments
See also Formal languages and automata.
The language $ \{ {x b x } : {x \in \{ a _ {1} , a _ {2} \} ^ {*} }\} $( see also above) takes $ n ^ {2} $ time on a no-worktape Turing machine, and, clearly, can be recognized in $ 2n $ time on a one-worktape Turing machine. For acceptance of context-sensitive languages by multi-worktape Turing machines better lower time bounds are known.
With respect to context-free languages the main achievement of the past decade has been the solution of the problem on the closure of context-sensitive languages under complementation. It was shown by N. Immerman [a3] and (independently) R. Szelepcsényi [a4] that the complement of a context-sensitive language is again context sensitive. In fact, the result holds for general classes of languages recognized by space-bounded non-deterministic Turing machines; the context-sensitive languages being the class of languages recognized by non-deterministic linear bounded automata being a typical example.
References
| [a1] | J.E. Hopcroft, J.D. Ulman, "Introduction to automata theory, languages and computation" , Addison-Wesley (1979) |
| [a2] | H.R. Lewis, C.H. Papadimitriou, "Elements of the theory of computation" , Prentice-Hall (1981) |
| [a3] | N. Immerman, "Nondeterministic space is closed under complementation" , Proc. 3-rd IEEE Conf. Structure in Complexity Theory (Georgetown, June) , IEEE (1988) pp. 112–115 |
| [a4] | R. Szelepcsényi, "The method of forcing for nondeterministic automata" EATCS Bulletin , 33 (1987) pp. 96–100 |
Grammar, context-sensitive. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Grammar,_context-sensitive&oldid=45540