Syntactic structure

A mathematical construction used in mathematical linguistics for describing the structure of sentences in a natural language. Two types of syntactic structure are most widely used — component systems and relations of syntactic subordination. The notion of a component system can be defined in the following way. Let $ x $ be a non-empty chain (a word) over an alphabet $ V $; in what follows, imbedded words (or letters, cf. Imbedded word) in the chain are called its points; a set of points of the chain of the form $ \{ x : a \leq x \leq b \} $, where $ a $ and $ b $ are fixed points, is called a segment of the chain. A set $ C $ of segments of a chain $ x $ is called a set of components of this chain if: 1) $ C $ contains a segment consisting of all points of $ x $, and all one-point segments of $ x $; and 2) any two segments of $ C $ either do not intersect, or one of them is contained in the other. The elements of $ C $ are called components. If the alphabet $ V $ is interpreted as the set of words in a natural language and $ x $ as a sentence, then by suitably choosing a component system for $ x $ the non-trivial components of $ C $( that is, those in $ C $ but not those of 1) above) represent word-combinations, i.e. groups of words that are intuitively perceived by one familiar with the language as "syntactically connected" pieces of a sentence. For example, the sentence

$$ \textrm{ The "union" of two closed sets is a closed set } $$

admits the following "natural" component system (the boundaries of non-trivial components are indicated by brackets):

$$ \textrm{ (((The union) (of (two (closed sets)))) (is (a (closed set)))) } . $$

If one equips a component system $ C $ with the relation of direct inclusion, then $ C $ is a rooted tree (where the roots are just the one-point components of $ x $), called the component tree. For the above example, it has the following form:

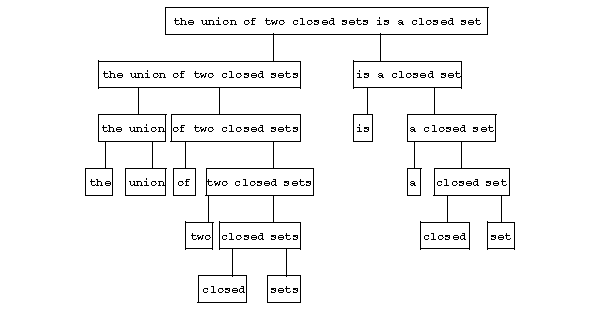
Figure: s091880a

Components usually carry labels, which are the "syntactic characteristics" of the word-combinations (a component can have more than one label). In the above example the component coinciding with the whole sentence is naturally labelled by the symbol SENT denoting "sentence" , the component "the union of two closed sets" by the symbol $ S _ {\textrm{ average } } $, denoting "a group of essential average type in the singular number and nominative case" , etc. The object thus obtained is a tree with labelled vertices, called a labelled component tree.

Another way of describing the structure of a sentence is to define on the set $ X $ of points of a chain $ x $ a binary relation $ \rightarrow $ in such a way that the graph $ ( X; \rightarrow ) $ is an (oriented) rooted tree. Such a relation is called a relation of (syntactic) subordination, and the corresponding tree the (syntactic) subordination tree. The notion of subordination is a formalization of that usually found in "school" grammars (in particular of the Russian language) concerning the subordination of some words in a sentence to others. In the graphical representation of a subordination tree, one usually arranges the points of the chain on a horizontal line and draw arrows above it. The above sentence has the following "natural" subordination tree:

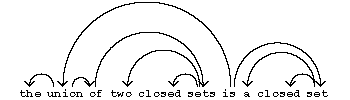
Figure: s091880b

(The root of a subordination tree is usually taken to be the predicate, as this is the organizing element of the sentence.)

The arrows in a subordination tree are often provided with labels indicating the types of syntactic relationship they represent. In our example, the relationship between "is" and "union" is naturally of the "predicative" type, and that between "sets" and "closed" is of the "determinating" type, etc.

The subordination trees of sentences occurring in commercial and scientific texts usually satisfy the so-called projectivity condition, which is formulated in terms of the above graphical representation as follows: There is a path to every point lying under a certain arrow from the source of that arrow. It follows from this that no two arrows intersect; this is sometimes called the weak projectivity condition. This condition is often violated in fiction, usually with a view to achieving a definite artistic effect.

One single sentence can admit several different "natural" component systems (subordination trees). This is most often found in cases when the sense of a sentence can be understood in different ways, and various component systems (subordination trees) correspond to various interpretations of its meaning (syntactic homonymy).

For example, the sentence "she took the people from London" can mean either "the Londoners were taken (from somewhere)" or "(some) people were taken from London" . The former sense gives the component system

$$ \textrm{ She (took (the (people (_ { } London)))) } $$

and subordination tree:

Figure: s091880c

The latter sense yields

$$ \textrm{ She (took (the people) (_ { } London)) } $$

and

Figure: s091880d

Given a subordination tree on a chain and a point $ \alpha $ of the chain, the set of points of the chain that are reachable by a path from $ \alpha $( including $ \alpha $ itself) is called the dependence group of the point $ \alpha $. Any set obtained from the dependence group of $ \alpha $ by removing the dependence groups of some (or all) points subordinate to $ \alpha $( i.e. targets of arrows from $ \alpha $) is called a truncated dependence group of $ \alpha $.

The component system $ C $ of a chain $ x $ and the subordination tree defined on $ x $ are said to be compatible if the dependence groups of all the points of $ x $ are components, and every component is the dependence group or a truncated dependence group of some point of $ x $. The "natural" component system and subordination tree of a given sentence with a given sense are usually compatible (see the examples above). A subordination tree with a compatible component system is projective. For a given component system, there can be more than one compatible subordination tree. But if one imposes a certain relation of "dominance" between the components, it is possible to construct a "natural" uniquely-defined subordination tree. This is done in the following way. Given the component system $ C $ of a chain $ x $, one associates with every component that is not a single point a preferred component in the set of directly included components in it, and call this its main component. Then the ordered pair $ ( C, C ^ \prime ) $, where $ C ^ \prime $ is the set of all main components, is called a hierarchical component system. A hierarchical component system is connected with a subordination tree if it is compatible with this tree and if for every component $ A $ that is not a single point, the root of the subtree corresponding to it in the subordination tree coincides with the root of the subtree corresponding to the main component associated of the directly included components in $ A $. The "natural" component system of a sentence in the "natural" hierarchy is usually connected with the "natural" subordination tree. Thus, if one equips the component system in the above example with a hierarchy in the following way:

$$ \textrm{ [(The [union]) (of [two [closed [sets]]])] [[is] (a [closed [set]])] } $$

(where the main components are distinguished by square brackets), then the resulting hierarchical component system is connected with the above subordination tree for this sentence.

Not all types of sentences permit a sufficiently adequate description in terms of component systems and subordination trees. In particular, difficulties can arise in the description of sentences containing word-combinations with "particularly close" intrinsic connections (for example, complex verb forms) and also composite constructions. Furthermore, to describe the structure of sentences and other parts of speech at "deeper" levels it becomes necessary to use graphs of a more complex form than trees. For a more adequate description of a language it is necessary to consider not only syntactic, but also so-called anaphoric connections, that is, connections between imbeddings of words that "name the same thing" , for example:

$$ \textrm{ if } f \textrm{ is a mapping of } E \textrm{ onto } F $$

$$ \textrm{ and there is an inverse mapping } f ^ { - 1 } , $$

$$ \textrm{ then the latter is a mapping of } F \textrm{ onto } E. $$

Other, more complex, concepts of a syntactic structure are being developed to cope with such connections.

References

[1]	L. Tesnière, "Eléments de syntaxe structurale" , Paris (1965)
[2]	E.V. Paducheva, Vopros. Yazykozn. , 2 (1964) pp. 99–113
[3]	A.V. Gladkii, Nauchno-Tekhn. Inform. (2) , 9 (1971) pp. 35–38
[4]	A.V. Gladkii, "Formal grammars and languages" , Moscow (1973) (In Russian)
[5]	A.V. Gladkii, Slavica , 17, 18 (1981)