Bohm-Aharonov effect

A phenomenon in which the topological non-triviality of a gauge field is measurable physically [a1]. Moreover, this topological non-triviality, which can be expressed as a number $ n $, say, is a global topological invariant and so is not expressible by a local formula; this latter point being in contrast to a simpler topological invariant such as the dimension of the underlying space, which is deducible locally.

To demonstrate this effect physically, one arranges that a non-simply-connected region $ \Omega $ of space has zero electromagnetic field $ F $. This electromagnetic field $ F $ is related to the gauge field $ A $ by the usual relation

$$ F = dA, $$

where the usual differential form language has been used for $ F $ and $ A $ so that, if $ x _ \mu $ are local coordinates on $ \Omega $, one has

$$ F = F _ {\mu \nu } dx ^ \mu \wedge dx ^ \nu \textrm{ and } A = A _ \mu dx ^ \mu . $$

Given this $ F $ and $ \Omega $, one can devise an experiment in which one measures a diffraction pattern associated with the parallel transport, or holonomy, of the gauge field $ A $ round a non-contractible loop $ C $ in $ \Omega $( cf. also Holonomy group). The action of parallel transport on multi-linear objects, viewed either as vectors, spinors, tensors, etc., or as sections of the appropriate bundles, is via the operator $ PT ( C ) $, where

$$ PT ( C ) = { \mathop{\rm exp} } \left [ \int\limits _ { C } A \right ] . $$

Differential topology provides immediately the means to see that $ PT ( C ) $ is non-trivial. The argument goes as follows: $ F = dA $ so that the vanishing of $ F $ gives

$$ dA = 0 \Rightarrow ( A = df \textrm{ locally } ) . $$

Hence $ A $ determines a de Rham cohomology class $ [ A ] $ and one has

$$ [ A ] \in H ^ {1} ( \Omega; \mathbf R ) . $$

It is clear from Stokes' theorem (cf. Stokes theorem) that the integral $ \int _ {C} A $ only depends on the homotopy class of the loop $ C $. In addition, the loop $ C $ determines a homology class $ [ C ] $, where

$$ [ C ] \in H _ {1} ( \Omega; \mathbf R ) . $$

This means that the integral $ \int _ {C} A $( which can be taken equal to the number $ n $) is just the dual pairing $ ( \bullet, \bullet ) $ between cohomology and homology, i.e.

$$ ( [ A ] , [ C ] ) = \int\limits _ { C } A . $$

An experiment to test this for the electromagnetic field was done in [a2]. The experimental setup is of the Young's slits type, where electrons replace photons and with the addition of a very thin solenoid. The electrons pass through the slits and on either side of the solenoid an interference pattern is then detected. The interference pattern is first measured with the solenoid off. This pattern is then found to change when the solenoid is switched on, even though the electrons always pass through a region where the field $ F $ is zero.

Mathematically speaking one realizes the solenoid by a cylinder $ L $ so that

$$ \Omega = \mathbf R ^ {3} - L \Rightarrow $$

$$ \Rightarrow H ^ {1} ( \Omega; \mathbf R ) = H ^ {1} ( \mathbf R ^ {3} - L; \mathbf R ) = \mathbf Z. $$

The loop $ C $ is the union of the electron paths $ P _ {1} $ and $ P _ {2} $.

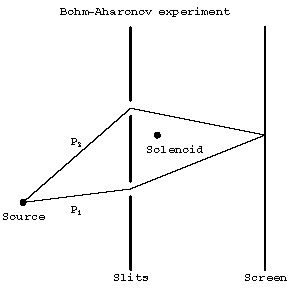
Figure: b110690a

A schematic Bohm–Aharonov experiment

The Bohm–Aharonov effect shows that the gauge potential $ A $ is a more basic object than the electromagnetic field $ F $.

Geometrically speaking, $ A $ is a connection and $ F $ is a curvature. Hence, in purely geometrical language one can describe the situation by saying that a flat connection (i.e. one for which $ F = 0 $, cf. Parallel displacement) need not be trivial if $ \Omega $ is not simply connected, i.e. if $ \pi _ {1} ( \Omega ) \neq 0 $. This non-triviality of flat connections when $ \pi _ {1} ( \Omega ) \neq 0 $ extends to the non-Abelian or Yang–Mills case.

For a Yang–Mills $ G $- connection $ A $( with $ G $ non-Abelian), the curvature $ F $ is given by

$$ F = dA + A \wedge A . $$

Further, if $ A $ is defined on a bundle $ P $ over a manifold $ \Omega $ and if it is assumed that, as in the Abelian case,

$$ F = 0 \textrm{ and } \pi _ {1} ( \Omega ) \neq 0, $$

then the integral $ \int _ {C} A $ only depends on the homotopy class of $ C $, which is also denoted by $ [ C ] $( the context should prevent any confusion with homology classes). Adding to this the fact that the parallel transport operator $ PT ( C ) = { \mathop{\rm exp} } [ \int _ {C} A ] $ has the property that $ PT ( C ) \in G $, one can use $ A $ to define the following linear mapping:

$$ {M _ {A} } : {\pi _ {1} ( \Omega ) } \rightarrow G , [ C ] \mapsto PT ( C ) . $$

One can check that $ M _ {A} \in { \mathop{\rm Hom} } ( \pi _ {1} ( \Omega ) ,G ) $ so that, as $ [ C ] $ varies, the flat $ G $- connection $ A $ on $ \Omega $ gives a representation of the fundamental group $ \pi _ {1} ( \Omega ) $ in $ G $; it is easy to verify that if $ A \mapsto A _ {g} = g ^ {- 1 } Ag + g ^ {- 1 } dg $ under a gauge transformation $ g \in G $, then this $ g $ acts on $ PT ( C ) $ via the adjoint action $ { \mathop{\rm Ad} } ( G ) $. In other words, it acts by conjugation, i.e., $ PT ( C ) \mapsto g ^ {- 1 } PT ( C ) g $. But this means that the representations defined by $ M _ {A} $ and $ M _ {A _ {g} } $ are equivalent, thus the gauge equivalence class of flat connections $ [ A ] $ is characterized by an element of the quotient

$$ { \mathop{\rm Hom} } ( \pi _ {1} ( \Omega ) ,G ) / { \mathop{\rm Ad} } ( G ) . $$

Hence the moduli space of gauge-inequivalent flat connections is the space

$$ { \mathop{\rm Hom} } ( \pi _ {1} ( \Omega ) ,G ) / { \mathop{\rm Ad} } ( G ) . $$

The holonomy group element $ PT ( C ) $ is also of central interest elsewhere. It occurs in the study of the adiabatic periodic change of parameters of a quantum system described in quantum field theory, [a3], [a4], where it is called a Wilson line or Wilson loop, and in mathematics. One of the most important of these concerns the quantum field theory formulation of knot invariants [a5], such as the Jones polynomial [a6]. Flat connections also play a distinguished part in this theory.

See also Quantum field theory; Knot theory.

References

[a1]	Y. Aharonov, D. Bohm, "Significance of electromagnetic potentials in quantum theory" Phys. Rev. , 115 (1959) pp. 485–491
[a2]	D.R. Brill, F.G. Werner, "Significance of electromagnetic potentials in the quantum theory in the interpretation of electron fringe interferometer observations" Phys. Rev. Lett. , 4 (1960) pp. 344–347
[a3]	M.V. Berry, "Quantal phase factors accompanying adiabatic changes" Proc. Roy. Soc. London A , 392 (1984) pp. 45–57
[a4]	B. Simon, "Holonomy, the quantum adiabatic theorem and Berry's phase" Phys. Rev. Lett. , 51 (1983) pp. 2167–2170
[a5]	E. Witten, "Topological quantum field theory" Comm. Math. Phys. , 117 (1988) pp. 353–386
[a6]	V.F.R. Jones, "A polynomial invariant for knots via von Neumann algebras" Bull. Amer. Math. Soc. , 12 (1985) pp. 103–111

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️