Difference between revisions of "Universal space"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | A [[Topological space|topological space]] containing a homeomorphic image of every topological space of a certain class. Examples are: 1) | + | <!-- |
| + | u0957601.png | ||
| + | $#A+1 = 68 n = 3 | ||
| + | $#C+1 = 68 : ~/encyclopedia/old_files/data/U095/U.0905760 Universal space | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| + | |||
| + | {{TEX|auto}} | ||
| + | {{TEX|done}} | ||
| + | |||
| + | A [[Topological space|topological space]] containing a homeomorphic image of every topological space of a certain class. Examples are: 1) $ C [ 0 , 1 ] $, | ||
| + | cf. [[Banach space|Banach space]]; 2) the [[Hilbert cube|Hilbert cube]] and the [[Tikhonov cube|Tikhonov cube]]; 3) the Menger curve (cf. [[Line (curve)|Line (curve)]]); 4) the universal Milnor bundle (cf. [[Principal fibre bundle|Principal fibre bundle]]). | ||
The existence of universal spaces allows the consideration of abstract objects as subobjects (in the categorical sense) of a more concrete one, and thus endows them with a greater wealth of "intrinsic" properties. On the other hand, it emphasizes the relations of "parts of a whole" . | The existence of universal spaces allows the consideration of abstract objects as subobjects (in the categorical sense) of a more concrete one, and thus endows them with a greater wealth of "intrinsic" properties. On the other hand, it emphasizes the relations of "parts of a whole" . | ||
| Line 5: | Line 18: | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.M. Cohn, "Universal algebra" , Reidel (1981)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> P.M. Cohn, "Universal algebra" , Reidel (1981)</TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| Line 12: | Line 23: | ||
==Universal spaces in functional analysis.== | ==Universal spaces in functional analysis.== | ||
| − | There are various notions of a universal space in functional analysis. A topological vector space | + | There are various notions of a universal space in functional analysis. A topological vector space $ X _ {0} $ |
| + | is universal for a class $ {\mathcal X} $ | ||
| + | of topological vector spaces if for every $ X \in {\mathcal X} $ | ||
| + | there is a closed subspace of $ X _ {0} $ | ||
| + | isomorphic to $ X $. | ||
| + | There is always a trivial universal space for any class $ {\mathcal X} $, | ||
| + | but whether there is a universal space in $ {\mathcal X} $ | ||
| + | itself or in a closely related class is a different matter. The following theorem holds, [[#References|[a2]]]: There is a universal separable $ F $- | ||
| + | space for the class of all $ F ^ { * } $- | ||
| + | spaces. Here, an $ F $- | ||
| + | space and an $ F ^ { * } $- | ||
| + | space are defined as follows. | ||
| − | An | + | An $ F $- |
| + | norm on a linear space $ X $ | ||
| + | is a mapping $ \| \| $ | ||
| + | from $ X $ | ||
| + | to the non-negative real numbers such that: | ||
| − | 1) | + | 1) $ \| x \| = 0 $ |
| + | if and only if $ x= 0 $; | ||
| − | 2) | + | 2) $ \| ax \| = \| x \| $ |
| + | for all $ a $, | ||
| + | $ | a | = 1 $; | ||
| − | 3) | + | 3) $ \| x+ y \| \leq \| x \| + \| y \| $; |
| − | 4) | + | 4) $ \| a _ {n} x \| \rightarrow 0 $ |
| + | if $ a _ {n} \rightarrow 0 $; | ||
| − | 5) | + | 5) $ \| ax _ {n} \| \rightarrow 0 $ |
| + | if $ x _ {n} \rightarrow 0 $; | ||
| − | 6) | + | 6) $ \| a _ {n} x _ {n} \| \rightarrow 0 $ |
| + | if $ a _ {n} \rightarrow 0 $, | ||
| + | $ x _ {n} \rightarrow 0 $. | ||
| − | In conditions 4), 5), 6) the topology is the one induced by the translation-invariant metric | + | In conditions 4), 5), 6) the topology is the one induced by the translation-invariant metric $ \rho ( x, y)= \| x- y \| $. |
| + | If $ \| \| $ | ||
| + | is not required to satisfy 1), it is called an $ F $- | ||
| + | pseudo-norm. An $ F $- | ||
| + | norm or $ F $- | ||
| + | pseudo-norm is $ p $- | ||
| + | homogeneous if $ \| ax \| = | a | ^ {p} \| x \| $. | ||
| + | A $ 1 $- | ||
| + | homogeneous $ F $- | ||
| + | norm ( $ F $- | ||
| + | pseudo-norm) is a [[Norm|norm]] ([[Pseudo-norm|pseudo-norm]]). An $ F ^ { * } $- | ||
| + | space is a linear space with an $ F $- | ||
| + | norm; an $ F $- | ||
| + | space is a complete $ F ^ { * } $- | ||
| + | space. | ||
| − | Some other universality results: | + | Some other universality results: $ C[ 0, 1] $ |
| + | is universal for all separable Banach spaces (the Banach–Mazur theorem, cf. [[Metric space|Metric space]]); $ C( - \infty , \infty ) $ | ||
| + | is universal for all separable $ B _ {0} $- | ||
| + | spaces (a $ B _ {0} ^ { * } $- | ||
| + | space is a locally convex metric linear space and a $ B _ {0} $- | ||
| + | space is a complete $ B _ {0} ^ { * } $- | ||
| + | space); there is a separable locally pseudo-convex space which is universal for all separable locally pseudo-convex spaces; there is a separable locally bounded complete space $ X $ | ||
| + | with a $ p $- | ||
| + | homogeneous norm which is universal for all separable locally bounded spaces with $ p $- | ||
| + | homogeneous norms. (Here, an $ F $- | ||
| + | space is locally bounded if it contains a bounded neighbourhood of $ 0 $; | ||
| + | a locally pseudo-convex space is a metric linear space whose topology can be given by a family of $ p _ {n} $- | ||
| + | homogeneous pseudo-norms.) | ||
| − | The dual notion is that of a co-universal linear space. An | + | The dual notion is that of a co-universal linear space. An $ F $- |
| + | space $ X _ {0} $ | ||
| + | is co-universal for a family $ {\mathcal X} $ | ||
| + | of $ F $- | ||
| + | spaces if every element of $ {\mathcal X} $ | ||
| + | is isomorphic to a quotient space $ X _ {0} /Y $ | ||
| + | for a closed subspace $ Y $ | ||
| + | of $ X _ {0} $. | ||
| − | Some co-universality results: there is a separable | + | Some co-universality results: there is a separable $ F $- |
| + | space which is co-universal for all separable $ F $- | ||
| + | spaces, [[#References|[a2]]]; every separable locally bounded space $ X $ | ||
| + | with a $ p $- | ||
| + | homogeneous norm is an image of $ l _ {p} $ | ||
| + | under a continuous linear operator, [[#References|[a3]]]–[[#References|[a5]]]. | ||
Cf. [[#References|[a6]]] for a large number of universality and co-universality theorems for metric linear spaces, including all of the above. | Cf. [[#References|[a6]]] for a large number of universality and co-universality theorems for metric linear spaces, including all of the above. | ||
Revision as of 08:27, 6 June 2020
A topological space containing a homeomorphic image of every topological space of a certain class. Examples are: 1) $ C [ 0 , 1 ] $,
cf. Banach space; 2) the Hilbert cube and the Tikhonov cube; 3) the Menger curve (cf. Line (curve)); 4) the universal Milnor bundle (cf. Principal fibre bundle).
The existence of universal spaces allows the consideration of abstract objects as subobjects (in the categorical sense) of a more concrete one, and thus endows them with a greater wealth of "intrinsic" properties. On the other hand, it emphasizes the relations of "parts of a whole" .
References
| [1] | P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian) |
| [2] | P.M. Cohn, "Universal algebra" , Reidel (1981) |
Comments
There is also a dual notion of universal space: Every space in a certain class is a continuous image of the space in question. E.g., the Cantor set is universal for the class of compact metric spaces, the unit interval is universal for the class of locally connected continua (see Peano curve), and the pseudo-arc is universal for the class of snake-like continua (see Cube-like continuum).
Universal spaces in functional analysis.
There are various notions of a universal space in functional analysis. A topological vector space $ X _ {0} $ is universal for a class $ {\mathcal X} $ of topological vector spaces if for every $ X \in {\mathcal X} $ there is a closed subspace of $ X _ {0} $ isomorphic to $ X $. There is always a trivial universal space for any class $ {\mathcal X} $, but whether there is a universal space in $ {\mathcal X} $ itself or in a closely related class is a different matter. The following theorem holds, [a2]: There is a universal separable $ F $- space for the class of all $ F ^ { * } $- spaces. Here, an $ F $- space and an $ F ^ { * } $- space are defined as follows.
An $ F $- norm on a linear space $ X $ is a mapping $ \| \| $ from $ X $ to the non-negative real numbers such that:
1) $ \| x \| = 0 $ if and only if $ x= 0 $;
2) $ \| ax \| = \| x \| $ for all $ a $, $ | a | = 1 $;
3) $ \| x+ y \| \leq \| x \| + \| y \| $;
4) $ \| a _ {n} x \| \rightarrow 0 $ if $ a _ {n} \rightarrow 0 $;
5) $ \| ax _ {n} \| \rightarrow 0 $ if $ x _ {n} \rightarrow 0 $;
6) $ \| a _ {n} x _ {n} \| \rightarrow 0 $ if $ a _ {n} \rightarrow 0 $, $ x _ {n} \rightarrow 0 $.
In conditions 4), 5), 6) the topology is the one induced by the translation-invariant metric $ \rho ( x, y)= \| x- y \| $. If $ \| \| $ is not required to satisfy 1), it is called an $ F $- pseudo-norm. An $ F $- norm or $ F $- pseudo-norm is $ p $- homogeneous if $ \| ax \| = | a | ^ {p} \| x \| $. A $ 1 $- homogeneous $ F $- norm ( $ F $- pseudo-norm) is a norm (pseudo-norm). An $ F ^ { * } $- space is a linear space with an $ F $- norm; an $ F $- space is a complete $ F ^ { * } $- space.
Some other universality results: $ C[ 0, 1] $ is universal for all separable Banach spaces (the Banach–Mazur theorem, cf. Metric space); $ C( - \infty , \infty ) $ is universal for all separable $ B _ {0} $- spaces (a $ B _ {0} ^ { * } $- space is a locally convex metric linear space and a $ B _ {0} $- space is a complete $ B _ {0} ^ { * } $- space); there is a separable locally pseudo-convex space which is universal for all separable locally pseudo-convex spaces; there is a separable locally bounded complete space $ X $ with a $ p $- homogeneous norm which is universal for all separable locally bounded spaces with $ p $- homogeneous norms. (Here, an $ F $- space is locally bounded if it contains a bounded neighbourhood of $ 0 $; a locally pseudo-convex space is a metric linear space whose topology can be given by a family of $ p _ {n} $- homogeneous pseudo-norms.)
The dual notion is that of a co-universal linear space. An $ F $- space $ X _ {0} $ is co-universal for a family $ {\mathcal X} $ of $ F $- spaces if every element of $ {\mathcal X} $ is isomorphic to a quotient space $ X _ {0} /Y $ for a closed subspace $ Y $ of $ X _ {0} $.
Some co-universality results: there is a separable $ F $- space which is co-universal for all separable $ F $- spaces, [a2]; every separable locally bounded space $ X $ with a $ p $- homogeneous norm is an image of $ l _ {p} $ under a continuous linear operator, [a3]–[a5].
Cf. [a6] for a large number of universality and co-universality theorems for metric linear spaces, including all of the above.
References
| [a1] | R. Engelking, "General topology" , Heldermann (1989) |
| [a2] | N.J. Kalton, "Universal spaces and universal bases in metric linear spaces" Studia Math. , 61 (1977) pp. 161–191 |
| [a3] | J.H. Shapiro, "Examples of proper closed weakly dense subspaces in non-locally convex 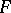 -spaces" Isr. J. Math. , 7 (1969) pp. 369–380 -spaces" Isr. J. Math. , 7 (1969) pp. 369–380 |
| [a4] | W.J. Stiles, "On properties of subspaces of 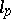 , ,  " Trans. Amer. Math. Soc. , 149 (1970) pp. 405–415 " Trans. Amer. Math. Soc. , 149 (1970) pp. 405–415 |
| [a5] | S. Banach, "Théorie des opérations linéaires" , PWN (1932) |
| [a6] | S. Rolewicz, "Metric linear spaces" , Reidel (1985) pp. 44 |
Universal space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Universal_space&oldid=49094