Topology of imbeddings
The branch of topology in which one studies local topological properties of dispositions of closed subsets of a Euclidean space or manifold.
The topology of imbeddings arose in the work of A. Schoenflies, L. Antoine, P.S. Urysohn, and J. Alexander. Imbeddings in $ E ^ {3} $ were studied in the 1950s. In particular, it was proved that an imbedding of a surface in $ E ^ {3} $ can be topologically approximated by a polyhedral imbedding. The systematic study of the topology of imbeddings in $ E ^ {n} $ for $ n > 3 $ began after the solution of the Schoenflies conjecture. Basically it came about in an environment of accumulation of facts and solutions to a large number of problems of a special character. Relations between methods of the theory of the topology of imbeddings and the geometric topology of manifolds were also clarified. At approximately the middle of the 1970s, the topology of imbeddings was formulated as an independent branch with its own themes, methods and problems. It was used to solve a number of basic problems in the geometric topology of manifolds: the existence was proved of a non-combinatorial triangulation of spheres of dimension $ \geq 5 $, the characterization of topological manifolds was obtained and the simply-connected four-dimensional manifolds were classified.
A topological imbedding of a space $ X $ (as a rule, a manifold, a polyhedron or a compact set) in a Euclidean space $ E ^ {n} $ is an arbitrary homeomorphism $ f: X \rightarrow E ^ {n} $ from $ X $ onto a space $ f ( X) \subset E ^ {n} $. Sometimes, a topological imbedding is simply understood to be an inclusion $ X \subset E ^ {n} $. Two imbeddings $ f _ {1} , f _ {2} : X \rightarrow E ^ {n} $ are said to be equivalent if there exists a homeomorphism $ h: E ^ {n} \rightarrow E ^ {n} $ such that $ h \circ f _ {1} = f _ {2} $. If $ h $ is an isotopy, then the imbeddings are said to be isotopic.
The simplest examples of non-equivalent imbeddings are obtained using knots (see Knot theory); it is much more difficult to construct non-equivalent imbeddings of zero-dimensional compacta or segments in $ E ^ {3} $ (see Wild knot).
A Cantor set on a rectilinear segment lying in $ E ^ {3} $ and a wild zero-dimensional Antoine compactum in $ E ^ {3} $ are non-equivalent.
The fact that the basic problems of the theory of topological imbeddings concentrate on local properties is explained by the existence of so-called wild imbeddings, for which the regularity of the local structure is destroyed. The study of global properties of tame (locally flat) imbeddings is, as a rule, not included in the topology of imbeddings (cf. also Tame imbedding).
The following four theorems may be considered as fundamental in the theory of topological imbeddings.
Theorem 1 (characterization).
An imbedding $ X \subset E ^ {n} $ is tame if and only if the complement $ Y = E ^ {n} \setminus X $ has the property 1-ULC (for an arbitrary $ \epsilon > 0 $ there exists a $ \delta > 0 $ such that each $ \delta $-mapping $ S ^ {1} \rightarrow Y $ is $ \epsilon $-homotopically zero in $ Y $).
Theorem 2 (on close imbeddings).
Any two close tame imbeddings are isotopic by a small isotopy.
Theorem 3 (on imbeddings in a trivial-dimensional domain).
If $ 2 \mathop{\rm dim} X + 2 \leq n $, then any two tame imbeddings are isotopic.
Theorem 4 (on approximation).
Any imbedding can be approximated by a tame imbedding. With the exception of theorem 3, all these theorems have been proved only under certain restrictions on the dimensions; these restrictions are different for manifolds, polyhedra and compacta.
An imbedding of a manifold $ X $ in $ E ^ {n} $ is said to be tame (or locally flat) if for an arbitrary point $ x \in X $ there exists a neighbourhood $ U ( x) $ in $ E ^ {n} $ such that the pair $ ( U ( x), U ( x) \cap X) $ is homeomorphic to the standard pair $ ( E ^ {n} , E ^ {r} ) $ under a homeomorphism transferring the point to the origin of $ E ^ {n} $.
Theorem 1 holds if $ n \neq 4 $ and $ r \neq n - 2 $ (if $ r = n - 2 $ and $ n \geq 5 $ the answer is also known: It is necessary for the complement $ Y = E ^ {n} \setminus X $ to be, roughly speaking, homotopically equivalent to a circle).
Theorem 2 holds if $ r \neq n - 2 $ and $ n \geq 5 $ (the addition of a small knot shows that for $ r = n - 2 $, theorem 2 is obviously false; a condition for two imbeddings to be isotopically close is known when $ r = n - 2 $). In addition, if $ X $ is the sphere $ S ^ {r} $, it has been proved that an arbitrary tame imbedding $ S ^ {r} \rightarrow E ^ {n} $ is isotopically standard if $ r \neq n - 2 $ (if $ r = n - 2 $ and $ n \neq 4 $ this is true if and only if the complement $ E ^ {n} \setminus S ^ {n - 2 } $ is homotopically equivalent to a circle).
Theorem 4 holds if $ r \neq n - 2 $ and $ n \neq 4 $ (moreover, if $ r = n - 2 $ and $ n \geq 6 $ this theorem — as corresponding counterexamples show — is obviously false).
An imbedding of a polyhedron $ X $ in $ E ^ {n} $ is said to be tame if it is equivalent to a piecewise-linear imbedding. Theorems 1, 2 and 3 hold if $ \mathop{\rm dim} X \leq n - 3 $.
An imbedding of an $ r $-dimensional compactum $ X $ in $ E ^ {n} $ is said to be tame if it is possible to remove it by an isotopy from an arbitrary rectilinear polyhedron $ P \subset E ^ {n} $ of dimension $ \leq n - r - 2 $. Theorem 1 holds if $ r \leq n - 3 $ and $ n \neq 4 $, theorem 2 is, generally speaking, false (if $ 2r + 2 > n $), while theorem 4 holds for arbitrary $ r $.
References
| [1] | L.V. Keldysh, "Topological imbeddings in a Euclidean space" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [2] | A.V. Chernavskii, "Locally homotopic unknotted imbeddings of manifolds" Soviet Math. Dokl. , 9 : 4 (1968) pp. 835–839 Dokl. Akad. Nauk SSSR , 181 : 2 (1968) pp. 290–293 |
| [3] | A.V. Chernavskii, "Coincidence of local flatness and local simple-connectedness for embeddings of (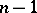 )-dimensional manifolds in )-dimensional manifolds in  -dimensional manifolds when -dimensional manifolds when 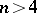 " Math. USSR Sb. , 20 (1973) pp. 297–304 Mat. Sb. , 91 : 2 (1973) pp. 279–286 " Math. USSR Sb. , 20 (1973) pp. 297–304 Mat. Sb. , 91 : 2 (1973) pp. 279–286 |
| [4] | R. Daverman, "Locally nice codimension one manifolds are locally flat" Bull. Amer. Math. Soc. , 79 : 2 (1973) pp. 410–413 |
| [5] | T. Chapman, "Locally homotopically unknotted embeddings of manifolds in codimension two are locally flat" Topology , 18 (1979) pp. 339–348 |
| [6] | F. Ancel, J. Cannon, "The locally flat approximation of cell-like embeddings" Ann. of Math. , 109 (1979) pp. 61–86 |
| [7] | J. Bryant, C.L. Seebeck, "Locally nice embeddings of polyhedra" Quart. J. Math. , 19 (1968) pp. 257–274 |
| [8] | R.D. Edwards, "The equivalence of close piecewise linear embeddings" General Topol. Appl. , 5 : 2 (1975) pp. 147–180 |
| [9] | R.T. Miller, "Approximating codimension three embeddings" Ann. of Math. , 95 : 3 (1972) pp. 406–416 |
| [10] | J.L. Bryant, "Approximating embeddings of polyhedra in codimension three" Trans. Amer. Math. Soc. , 170 (1972) pp. 85–95 |
| [11] | R.D. Edwards, "Dimension theory I" L.C. Glase (ed.) T.B. Rushing (ed.) , Geometric Topology (Utah, 1974) , Lect. notes in math. , 438 , Springer (1975) pp. 195–211 |
| [12] | M.A. Shtan'ko, "Approximation of compacta in codimension greater than two" Math. USSR Sb. , 19 : 4 (1973) pp. 615–626 Mat. Sb. , 90 : 4 (1973) pp. 625–636 |
Comments
The question of whether a given space admits an imbedding in a particular $ E ^ {n} $ and the classification of such imbeddings have been the subject of much research in algebraic topology. H. Whitney [a1] proved that every smooth $ n $-dimensional manifold can be imbedded in $ E ^ {2n} $ ($ n > 1 $). The theory of characteristic classes (cf. Characteristic class) yields necessary conditions for a given $ n $-manifold to imbed in lower dimensions. For example, real projective space of dimension $ n = 2 ^ {k} $ cannot be imbedded in $ E ^ {2n-} 1 $. A. Haeflinger [a2] gave sufficient conditions for certain ranges of dimension. W.-T. Wu [a3], [a4] has developed algebraic invariants for imbeddings of simplicial complexes.
Cf. also Tight and taut immersions.
References
| [a1] | H. Whitney, "The self-intersections of a smooth  -manifold in -manifold in 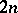 -space" Ann. of Math. , 45 (1944) pp. 220–246 -space" Ann. of Math. , 45 (1944) pp. 220–246 |
| [a2] | A. Haeflinger, "Plongements différentiables dans la domaine stable" Comm. Math. Helvetici , 37 (1963) pp. 155–176 |
| [a3] | W.-T. Wu, "On the realization of complexes in Euclidean spaces I" Scientia Sinica , 7 (1958) pp. 251–297 ((In Chinese; English abstract.)) |
| [a4] | W.-T. Wu, "On the realization of complexes in Euclidean spaces II" Scientia Sinica , 8 (1959) pp. 79–94 ((In Chinese; English abstract.)) |
| [a5] | E.E. Moise, "Geometric topology in dimensions 2 and 3" , Springer (1977) |
Topology of imbeddings. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Topology_of_imbeddings&oldid=51907