Wild knot
From Encyclopedia of Mathematics
A knot $L$ in the Euclidean space $E^3$ (cf. Knot theory) such that there is no homeomorphism of $E^3$ onto itself under which $L$ would become a closed polygonal line consisting of a finite number of segments.

Thus, knots containing the so-called Fox–Artin arcs — certain simple arcs obtained by a wild imbedding in $E^3$ — are wild. For example, the fundamental group $\pi_1(E^3\setminus L)$ is non-trivial for the arc $L_1$ (Fig. a); this group is trivial for the arc $L_2$ (Fig. b), but $E^3\setminus L_2$ itself is not homeomorphic to the complement of a point in $E^3$.
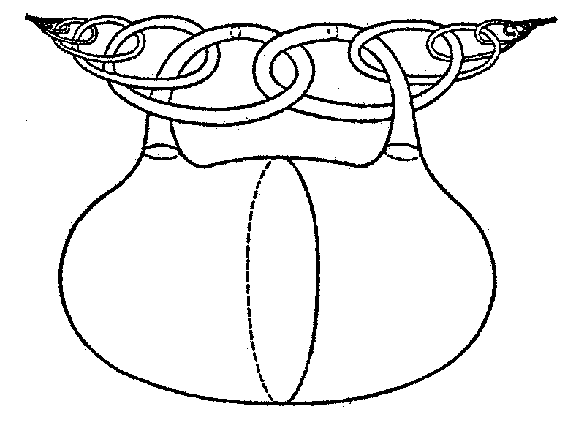
Figure: w097980b
For references see Wild sphere.
How to Cite This Entry:
Wild knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_knot&oldid=35622
Wild knot. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Wild_knot&oldid=35622
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article