Module
An Abelian group with the distributive action of a ring. A module is a generalization of a (linear) vector space over a field 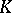 , when
, when 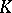 is replaced by a ring.
is replaced by a ring.
Let a ring 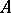 be given. An additive Abelian group
be given. An additive Abelian group 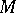 is called a left
is called a left 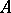 -module if there is a mapping
-module if there is a mapping 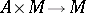 whose value on a pair
whose value on a pair 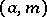 , for
, for 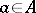 ,
, 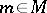 , written
, written 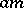 , satisfies the axioms:
, satisfies the axioms:
1) 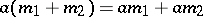 ;
;
2) 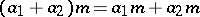 ;
;
3) 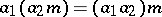 . If
. If 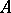 has a unit, then it is usual to require in addition that for any
has a unit, then it is usual to require in addition that for any 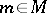 ,
,  . A module with this property is called unitary or unital (cf. Unitary module).
. A module with this property is called unitary or unital (cf. Unitary module).
Right 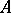 -modules are defined similarly; axiom 3) is replaced by
-modules are defined similarly; axiom 3) is replaced by 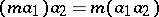 . Any right
. Any right 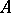 -module can be considered as a left
-module can be considered as a left 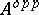 -module over the opposite ring
-module over the opposite ring 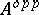 anti-isomorphic to
anti-isomorphic to 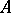 ; hence, corresponding to any result about right
; hence, corresponding to any result about right 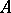 -modules there is a result about left
-modules there is a result about left 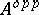 -modules, and conversely. When
-modules, and conversely. When 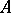 is commutative, any left
is commutative, any left 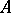 -module can be considered as a right
-module can be considered as a right 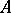 -module and the distinction between left and right modules disappears. Below only left
-module and the distinction between left and right modules disappears. Below only left 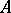 -modules are discussed.
-modules are discussed.
The simplest examples of modules (finite Abelian groups; they are 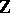 -modules) were known already to C.F. Gauss as class groups of binary quadratic forms. The general notion of a module was first encountered in the 1860's till 1880's in the work of R. Dedekind and L. Kronecker, devoted to the arithmetic of algebraic number and function fields. At approximately the same time research on finite-dimensional associative algebras, in particular, group algebras of finite groups (B. Pierce, F. Frobenius), led to the study of ideals of certain non-commutative rings. At first the theory of modules was developed primarily as a theory of ideals of a ring. Only later, in the work of E. Noether and W. Krull, it was observed that it was more convenient to formulate and prove many results in terms of arbitrary modules, and not just ideals. Subsequent developments of the theory of modules were connected with the application of methods and ideas of the theory of categories (cf. Category), in particular, methods of homological algebra.
-modules) were known already to C.F. Gauss as class groups of binary quadratic forms. The general notion of a module was first encountered in the 1860's till 1880's in the work of R. Dedekind and L. Kronecker, devoted to the arithmetic of algebraic number and function fields. At approximately the same time research on finite-dimensional associative algebras, in particular, group algebras of finite groups (B. Pierce, F. Frobenius), led to the study of ideals of certain non-commutative rings. At first the theory of modules was developed primarily as a theory of ideals of a ring. Only later, in the work of E. Noether and W. Krull, it was observed that it was more convenient to formulate and prove many results in terms of arbitrary modules, and not just ideals. Subsequent developments of the theory of modules were connected with the application of methods and ideas of the theory of categories (cf. Category), in particular, methods of homological algebra.
Examples of modules.
1) Any Abelian group 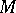 is a module over the ring of integers
is a module over the ring of integers 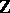 . For
. For 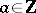 and
and 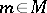 the product
the product 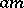 is defined as the result of adding
is defined as the result of adding  to itself
to itself  times.
times.
2) When 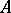 is a field, the notion of a unitary
is a field, the notion of a unitary 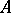 -module is exactly equivalent to the notion of a linear vector space over
-module is exactly equivalent to the notion of a linear vector space over 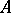 .
.
3) An  -dimensional vector space
-dimensional vector space 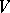 over a field
over a field 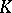 (provided with coordinates) can be considered as a module over the ring
(provided with coordinates) can be considered as a module over the ring 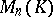 of all
of all 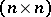 -matrices with coefficients in
-matrices with coefficients in 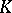 . For
. For 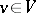 and
and 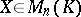 the product
the product  is defined as multiplication of the matrix
is defined as multiplication of the matrix 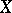 by the column of coordinates of the vector
by the column of coordinates of the vector  .
.
4) An associative ring (cf. Associative rings and algebras) 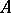 is a left
is a left 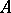 -module. Multiplication of elements of the ring by elements of the module is ordinary multiplication in
-module. Multiplication of elements of the ring by elements of the module is ordinary multiplication in 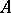 .
.
5) The set of differential forms on a smooth manifold 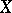 has the natural structure of a module over the ring of all smooth functions on
has the natural structure of a module over the ring of all smooth functions on 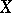 .
.
6) Connected with any Abelian group 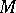 is the associative ring with identity,
is the associative ring with identity, 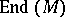 , of all endomorphisms of
, of all endomorphisms of 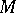 . The group
. The group 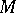 has a natural
has a natural 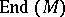 -module structure.
-module structure.
If there is an 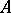 -module structure on
-module structure on 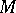 , for some ring
, for some ring 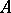 , then the mapping
, then the mapping 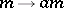 is an endomorphism of
is an endomorphism of 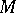 for any
for any 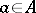 . Associating with the element
. Associating with the element 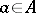 the endomorphism of
the endomorphism of 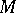 that it generates, one obtains a homomorphism
that it generates, one obtains a homomorphism 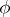 of
of 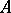 into
into 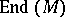 . Conversely, any homomorphism
. Conversely, any homomorphism 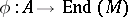 defines the structure of an
defines the structure of an 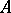 -module on
-module on 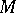 . Thus, the specification of an
. Thus, the specification of an 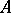 -module structure on an Abelian group
-module structure on an Abelian group 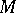 is equivalent to the specification of a homomorphism of rings
is equivalent to the specification of a homomorphism of rings 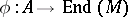 . Such a homomorphism is also called a representation of the ring
. Such a homomorphism is also called a representation of the ring 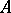 , and
, and 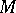 is called a representation module. Connected with any representation
is called a representation module. Connected with any representation 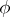 is a two-sided ideal
is a two-sided ideal 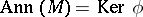 , consisting of the
, consisting of the 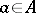 such that
such that 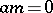 for all
for all 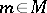 . This ideal is called the annihilator of the module
. This ideal is called the annihilator of the module 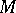 . When
. When 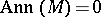 , the representation is called faithful and
, the representation is called faithful and 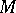 is called a faithful module (or faithful representation).
is called a faithful module (or faithful representation).
It is obvious that a module 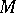 can also be considered as a module over the quotient ring
can also be considered as a module over the quotient ring 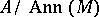 . In particular, although the definition of a module does not assume the associativity of
. In particular, although the definition of a module does not assume the associativity of 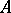 , the ring
, the ring  is always associative. Therefore, in the majority of cases the discussion may be restricted to modules over associative rings. Everywhere below, unless stated otherwise,
is always associative. Therefore, in the majority of cases the discussion may be restricted to modules over associative rings. Everywhere below, unless stated otherwise, 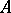 is assumed to be associative.
is assumed to be associative.
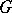 -modules.
-modules.
Let 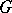 be a group. An additive Abelian group
be a group. An additive Abelian group 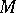 is called a left
is called a left 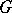 -module if there is a mapping
-module if there is a mapping 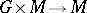 whose value at a pair
whose value at a pair 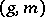 , where
, where 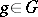 ,
, 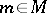 , is written as
, is written as 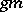 , and where for any
, and where for any 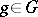 the mapping
the mapping 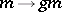 is an endomorphism of
is an endomorphism of 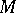 ; for any
; for any  ,
, 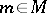 ,
, 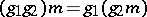 ; and for all
; and for all 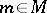 ,
, 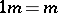 , where 1 is the identity of
, where 1 is the identity of 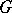 . For any
. For any 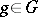 the mapping
the mapping 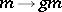 is an automorphism of the group
is an automorphism of the group 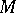 .
.
Right 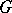 -modules may be defined similarly.
-modules may be defined similarly.
Examples of 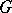 -modules.
-modules.
1) Let 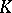 be a Galois extension of a field
be a Galois extension of a field 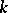 with Galois group
with Galois group 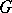 . Then the additive and multiplicative groups of
. Then the additive and multiplicative groups of 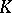 have the natural structure of
have the natural structure of 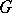 -modules. If
-modules. If 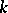 is an algebraic number field, then other
is an algebraic number field, then other 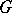 -modules are: the additive group of the ring of integers of
-modules are: the additive group of the ring of integers of 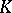 , the group of units of
, the group of units of 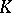 , the group of divisors and the divisor class group of
, the group of divisors and the divisor class group of 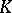 , etc. A module over a Galois group is called a Galois module.
, etc. A module over a Galois group is called a Galois module.
2) Let an extension of an Abelian group 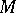 be given, that is, an exact sequence of groups
be given, that is, an exact sequence of groups
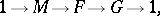 |
where 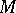 is an Abelian normal subgroup of
is an Abelian normal subgroup of 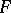 and
and 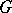 is an arbitrary group. Then
is an arbitrary group. Then 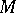 can be given the natural structure of a
can be given the natural structure of a 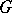 -module by putting, for
-module by putting, for 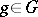 ,
, 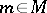 ,
, 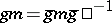 , where
, where 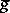 is an inverse image of
is an inverse image of 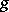 in
in 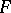 .
.
When the group operation in the Abelian group  is written multiplicatively (for example, if
is written multiplicatively (for example, if 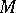 is the multiplicative group of a field), the notation
is the multiplicative group of a field), the notation 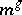 is also used instead of
is also used instead of 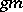 , that is, the action of
, that is, the action of 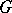 is written exponentially.
is written exponentially.
Let a 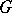 -module
-module 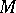 be given. By associating with an element
be given. By associating with an element 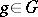 the automorphism
the automorphism 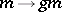 of
of 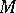 , a homomorphism of
, a homomorphism of 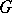 into the group of invertible elements of the ring
into the group of invertible elements of the ring  is obtained. Conversely, any homomorphims of
is obtained. Conversely, any homomorphims of 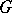 into the group of invertible elements of
into the group of invertible elements of 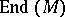 gives
gives 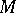 the structure of a
the structure of a 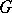 -module.
-module.
The notions of a module over a ring and a 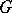 -module are closely connected. Namely, any
-module are closely connected. Namely, any 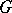 -module
-module 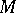 can be regarded as a module over the group ring (cf. Group algebra)
can be regarded as a module over the group ring (cf. Group algebra) 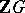 if the action of
if the action of 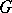 on
on 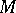 is extended linearly, that is, if one puts
is extended linearly, that is, if one puts
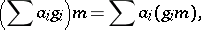 |
where 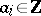 ,
, 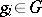 ,
, 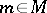 . Conversely, given a unitary
. Conversely, given a unitary 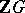 -module structure on
-module structure on 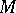 ,
, 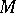 may be regarded to be a
may be regarded to be a 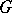 -module.
-module.
When 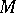 is simultaneously a
is simultaneously a 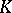 -module over a commutative ring
-module over a commutative ring 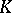 and a
and a 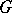 -module, where the action of the elements of
-module, where the action of the elements of 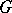 on
on 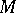 commutes with the action of the elements of
commutes with the action of the elements of 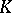 , then
, then 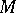 may be given the structure of a
may be given the structure of a 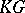 -module by linearly extending the action from
-module by linearly extending the action from 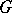 to
to 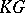 . For example, if
. For example, if 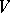 is a linear vector space over a field
is a linear vector space over a field 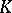 , then the specification of a
, then the specification of a 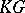 -module structure on
-module structure on 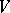 is equivalent to giving a representation of
is equivalent to giving a representation of 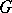 in
in 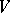 .
.
Using the standard involution 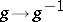 in
in 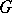 , any left
, any left 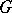 -module
-module 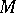 can be made into a right
can be made into a right 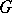 -module by putting
-module by putting 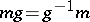 for
for 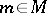 ,
, 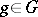 . Similarly, any right
. Similarly, any right 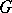 -module can be made into a left
-module can be made into a left 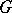 -module.
-module.
Modules over a Lie algebra.
Let 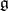 be a Lie algebra over a commutative ring
be a Lie algebra over a commutative ring 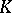 and let
and let 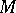 be a
be a 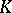 -module. The specification of a
-module. The specification of a 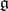 -module structure on
-module structure on 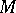 consists of the specification of a
consists of the specification of a 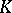 -endomorphism
-endomorphism 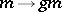 of the group
of the group 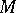 for each
for each 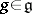 , where the axiom
, where the axiom
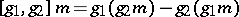 |
holds for 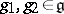 ,
, 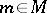 . This definition differs from that of an
. This definition differs from that of an 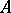 -module given earlier. Giving a
-module given earlier. Giving a 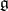 -module structure on
-module structure on 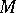 is equivalent to giving a Lie algebra homomorphism of
is equivalent to giving a Lie algebra homomorphism of 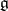 into the Lie algebra of the ring
into the Lie algebra of the ring 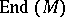 . A module over a Lie algebra
. A module over a Lie algebra 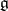 may also be regarded as a module in the usual sense over the universal enveloping algebra of
may also be regarded as a module in the usual sense over the universal enveloping algebra of 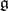 .
.
Constructions in the theory of modules.
Starting from a given 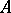 -module it is possible to obtain new
-module it is possible to obtain new 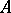 -modules by a number of standard constructions. Thus, with any module
-modules by a number of standard constructions. Thus, with any module 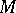 is associated the lattice of its submodules. For example, if
is associated the lattice of its submodules. For example, if 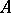 is considered as left module over itself, then its left submodules are precisely the left ideals in
is considered as left module over itself, then its left submodules are precisely the left ideals in 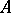 . A number of important types of modules are defined in terms of the lattice of submodules. For example, the condition for termination of a descending (ascending) chain of submodules defines Artinian modules (respectively, Noetherian modules, cf. Artinian module; Noetherian module). The condition for absence of non-trivial submodules, that is, submodules other than 0 or
. A number of important types of modules are defined in terms of the lattice of submodules. For example, the condition for termination of a descending (ascending) chain of submodules defines Artinian modules (respectively, Noetherian modules, cf. Artinian module; Noetherian module). The condition for absence of non-trivial submodules, that is, submodules other than 0 or 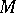 , defines irreducible or simple modules (cf. Irreducible module).
, defines irreducible or simple modules (cf. Irreducible module).
For a module 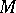 and any submodule
and any submodule 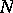 , the quotient group
, the quotient group 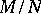 can be given the structure of an
can be given the structure of an 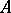 -module. This module is called the quotient module of
-module. This module is called the quotient module of 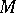 over
over 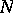 .
.
A homomorphism of 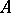 -modules is defined as an Abelian group homomorphism
-modules is defined as an Abelian group homomorphism 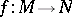 commuting with multiplication by elements of
commuting with multiplication by elements of 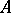 , that is,
, that is, 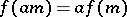 for all
for all 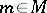 ,
, 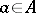 . If two homomorphisms
. If two homomorphisms 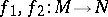 are given, then their sum, defined by
are given, then their sum, defined by 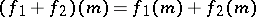 , is again a homomorphism of
, is again a homomorphism of 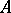 -modules. This addition gives an Abelian group structure to the set
-modules. This addition gives an Abelian group structure to the set 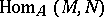 of all homomorphisms of
of all homomorphisms of 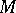 into
into 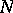 . For any homomorphism
. For any homomorphism 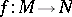 the submodules
the submodules 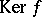 (the kernel of
(the kernel of 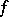 ) and
) and 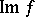 (the image of
(the image of 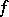 ), and also the quotient modules
), and also the quotient modules 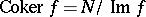 (the cokernel of
(the cokernel of 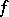 ) and
) and 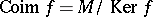 (the coimage of
(the coimage of 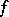 ) are defined. The modules
) are defined. The modules 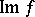 and
and 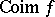 are canonically isomorphic and therefore usually identified. For example, for any left ideal
are canonically isomorphic and therefore usually identified. For example, for any left ideal 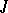 of
of 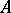 the quotient module
the quotient module 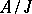 is defined. The module
is defined. The module 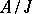 is irreducible if and only if
is irreducible if and only if 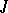 is a maximal left ideal (cf. Maximal ideal). If
is a maximal left ideal (cf. Maximal ideal). If 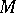 is an irreducible
is an irreducible 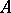 -module not annihilating the ring
-module not annihilating the ring 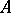 , then
, then 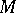 is isomorphic to
is isomorphic to 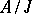 for some maximal left ideal
for some maximal left ideal 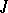 .
.
For any family of 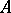 -modules
-modules 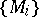 , where
, where 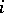 runs through some index set
runs through some index set 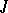 , the direct sum and direct product of
, the direct sum and direct product of 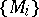 exist in the category of
exist in the category of 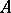 -modules. Here an element of the direct product
-modules. Here an element of the direct product 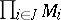 may be interpreted as a vector
may be interpreted as a vector 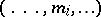 the components of which are indexed by
the components of which are indexed by 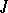 and where for each
and where for each 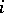 ,
, 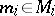 . The sum of such vectors and their multiplication by elements of the ring are defined componentwise. The direct sum
. The sum of such vectors and their multiplication by elements of the ring are defined componentwise. The direct sum 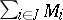 of the family
of the family 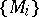 can be interpreted as the submodule of the direct product consisting of the vectors all components of which, except for finitely many, are equal to zero.
can be interpreted as the submodule of the direct product consisting of the vectors all components of which, except for finitely many, are equal to zero.
For a projective (inductive) system of 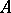 -modules the projective (inductive) limit of this system can be naturally equipped with the structure of an
-modules the projective (inductive) limit of this system can be naturally equipped with the structure of an  -module. The direct product and direct sum may be considered as special cases of the notions of a projective and an inductive limit.
-module. The direct product and direct sum may be considered as special cases of the notions of a projective and an inductive limit.
Generators and relations.
Let 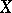 be a subset of an
be a subset of an 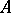 -module
-module 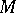 . The submodule generated by
. The submodule generated by 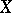 is the intersection of the submodules of
is the intersection of the submodules of 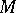 which contain
which contain 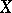 . If this submodule coincides with
. If this submodule coincides with 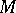 , then
, then 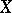 is called a family (system) of generators of the module
is called a family (system) of generators of the module 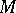 . A module admitting a finite family of generators is called a finitely-generated module. For example, in a Noetherian ring any ideal is a finitely-generated module. A direct sum of a finite number of finitely-generated modules is again finitely generated. Any quotient module of a finitely-generated module is also finitely generated. For the construction of a system of generators for a module
. A module admitting a finite family of generators is called a finitely-generated module. For example, in a Noetherian ring any ideal is a finitely-generated module. A direct sum of a finite number of finitely-generated modules is again finitely generated. Any quotient module of a finitely-generated module is also finitely generated. For the construction of a system of generators for a module 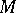 , Nakayama's lemma often turns out to be useful: For any ideal
, Nakayama's lemma often turns out to be useful: For any ideal 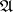 contained in the radical of a ring
contained in the radical of a ring 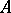 the condition
the condition 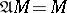 implies
implies 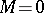 . In particular, under the conditions of Nakayama's lemma elements
. In particular, under the conditions of Nakayama's lemma elements  form a system of generators for
form a system of generators for 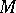 if their images generate the module
if their images generate the module 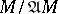 . This is used particularly often when
. This is used particularly often when  is a local ring and
is a local ring and 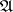 is the maximal ideal in
is the maximal ideal in 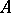 .
.
Let 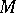 be a module with system of generators
be a module with system of generators 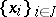 . Then a mapping
. Then a mapping 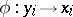 defines an epimorphism of the free
defines an epimorphism of the free 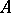 -module
-module 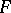 with generators
with generators 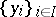 onto
onto 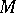 (
(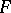 can be defined as the set of formal finite sums
can be defined as the set of formal finite sums 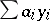 ,
,  , and
, and 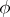 is extended from the generators to
is extended from the generators to 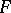 by linearity). The elements of
by linearity). The elements of 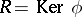 are called relations between the generators
are called relations between the generators 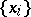 of
of 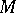 . If
. If 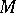 can be represented as a quotient module of a finitely-generated free module
can be represented as a quotient module of a finitely-generated free module 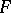 so that the module of relations
so that the module of relations 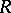 is also finitely generated, then
is also finitely generated, then 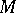 is called a finitely-presented module. For example, over a Noetherian ring
is called a finitely-presented module. For example, over a Noetherian ring 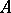 any finitely-generated module is finitely presented. In general, being finitely generated does not imply being finitely presented.
any finitely-generated module is finitely presented. In general, being finitely generated does not imply being finitely presented.
Change of rings.
There are standard constructions which allow an 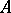 -module
-module 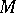 to be considered as a module over some other ring. For example, let
to be considered as a module over some other ring. For example, let 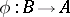 be a homomorphism of rings. Then, putting
be a homomorphism of rings. Then, putting 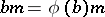 ,
, 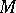 can be considered as a
can be considered as a 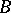 -module. The resulting
-module. The resulting 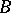 -module is said to be obtained by base change or, in particular in the case that
-module is said to be obtained by base change or, in particular in the case that 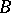 is a subring of
is a subring of 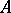 , by restriction of scalars. If
, by restriction of scalars. If 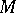 is a unitary
is a unitary 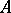 -module and
-module and 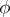 takes the identity to the identity,
takes the identity to the identity, 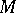 becomes a unitary
becomes a unitary 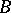 -module.
-module.
Let a ring homomorphism 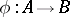 and an
and an 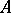 -module
-module 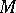 be given. Then
be given. Then 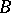 may be given the structure of a
may be given the structure of a 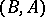 -module (cf. Bimodule) by putting
-module (cf. Bimodule) by putting 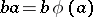 for
for 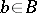 ,
, 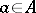 , and the left
, and the left  -module
-module 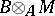 can be considered. One says that this module is obtained from
can be considered. One says that this module is obtained from 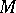 by extension of scalars.
by extension of scalars.
The category of modules.
The class of all modules over a given ring 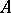 with homomorphisms of modules as morphisms forms an Abelian category, denoted, for instance, by
with homomorphisms of modules as morphisms forms an Abelian category, denoted, for instance, by 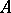 -mod or
-mod or 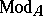 . The most important functors defined on this category are
. The most important functors defined on this category are 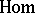 (homomorphism) and
(homomorphism) and 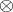 (tensor product). The functor
(tensor product). The functor 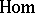 takes values in the category of Abelian groups and associates to a pair of
takes values in the category of Abelian groups and associates to a pair of 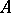 -modules
-modules 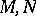 the group
the group 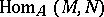 . For
. For 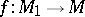 and
and 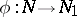 the mappings
the mappings
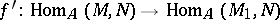 |
and
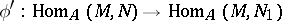 |
are defined in the obvious way; that is, the functor 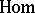 is contravariant in its first argument and covariant in the second. When
is contravariant in its first argument and covariant in the second. When 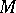 or
or 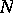 carry a bimodule structure, the group
carry a bimodule structure, the group 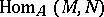 has an additional module structure. If
has an additional module structure. If 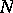 is an
is an 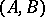 -module,
-module, 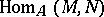 is a right
is a right 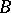 -module and if
-module and if 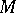 is an
is an 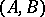 -module, then
-module, then 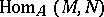 is a left
is a left 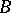 -module.
-module.
The functor 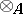 takes a pair
takes a pair 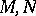 , where
, where 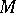 is a right
is a right 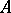 -module and
-module and 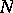 is a left
is a left 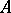 -module, to the tensor product
-module, to the tensor product 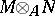 of
of 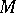 and
and 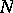 over
over 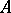 . This functor takes values in the category of Abelian groups and is covariant with respect to both
. This functor takes values in the category of Abelian groups and is covariant with respect to both 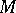 and
and 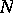 . When
. When 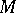 or
or 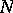 is a bimodule, the group
is a bimodule, the group 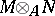 may be equipped with an additional structure. Namely, if
may be equipped with an additional structure. Namely, if 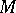 is a
is a 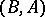 -module,
-module, 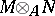 is a
is a 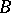 -module, and if
-module, and if 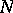 is an
is an 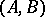 -module, then
-module, then 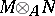 is a right
is a right 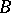 -module. The study of the functors
-module. The study of the functors 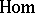 and
and  , and also of their derived functors, is one of the fundamental problems of homological algebra.
, and also of their derived functors, is one of the fundamental problems of homological algebra.
Many important types of modules can be characterized in terms of 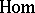 and
and 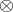 . Thus, a projective module
. Thus, a projective module 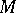 is defined by the requirement that the functor
is defined by the requirement that the functor 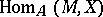 (as a functor in
(as a functor in 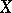 ) is exact (cf. Exact functor). Similarly, an injective module
) is exact (cf. Exact functor). Similarly, an injective module 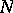 is defined by the requirement of exactness of
is defined by the requirement of exactness of 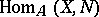 (in
(in 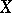 ). A flat module
). A flat module 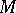 is defined by the requirement of exactness of the functor
is defined by the requirement of exactness of the functor 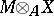 .
.
A module over a given ring 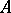 can be considered from two points of view.
can be considered from two points of view.
A) Modules can be studied from the point of view of their intrinsic structure. The fundamental problem here is the complete classification of modules, that is, the construction for each module of a system of invariants which characterizes the module up to an isomorphism, and, given a set of invariants, the ability to construct a module with those invariants. For certain types of rings such a description is possible. For example, if 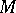 is a finitely-generated module over the group ring
is a finitely-generated module over the group ring 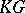 of a finite group
of a finite group 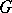 , where
, where 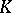 is a field of characteristic coprime with the order of
is a field of characteristic coprime with the order of 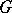 , then
, then 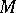 is representable as a finite direct sum of irreducible submodules (
is representable as a finite direct sum of irreducible submodules (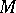 is completely reducible, cf. Completely-reducible module). This representation is unique up to an isomorphism (the choice of the irreducible modules is, in general, not unique). All irreducible submodules also admit a simple description: All of them are contained in the regular representation of
is completely reducible, cf. Completely-reducible module). This representation is unique up to an isomorphism (the choice of the irreducible modules is, in general, not unique). All irreducible submodules also admit a simple description: All of them are contained in the regular representation of 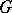 and are in one-to-one correspondence with the irreducible characters of the group. Modules over principal ideal rings and over Dedekind rings also have a simple description. Namely, any finitely-generated module
and are in one-to-one correspondence with the irreducible characters of the group. Modules over principal ideal rings and over Dedekind rings also have a simple description. Namely, any finitely-generated module 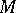 over a principal ideal ring
over a principal ideal ring 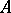 is isomorphic to a finite direct sum of modules of the form
is isomorphic to a finite direct sum of modules of the form 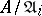 , where
, where 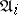 are ideals of
are ideals of 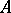 (possibly null), and where
(possibly null), and where 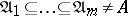 . The ideals
. The ideals 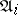 are uniquely determined by this last condition. Thus, the set of invariants
are uniquely determined by this last condition. Thus, the set of invariants 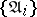 completely determines
completely determines 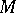 . If
. If 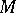 is a finitely-generated module over a Dedekind ring
is a finitely-generated module over a Dedekind ring 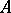 , then
, then 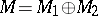 , where
, where 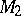 is a torsion module (periodic module) and
is a torsion module (periodic module) and 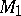 is a torsion-free module (the choice of
is a torsion-free module (the choice of 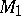 is not unique). The module
is not unique). The module 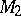 is annihilated by some ideal
is annihilated by some ideal 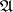 of
of 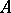 and, consequently, is a module over the principal ideal ring
and, consequently, is a module over the principal ideal ring 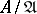 and admits the description given above;
and admits the description given above; 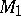 is representable in the form
is representable in the form 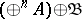 , where
, where 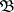 is an ideal of
is an ideal of 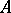 and
and 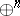 is the
is the  -fold direct sum. The module
-fold direct sum. The module 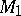 is, up to an isomorphism, determined by two invariants: the number
is, up to an isomorphism, determined by two invariants: the number  and the class of
and the class of 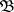 in the ideal class group.
in the ideal class group.
B) Another approach to the study of modules consists of studying the category 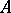 -mod and in considering a given module
-mod and in considering a given module 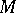 as an object of this category. Such a study is the object of homological algebra and algebraic
as an object of this category. Such a study is the object of homological algebra and algebraic 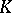 -theory. On this route many important and deep results have been found.
-theory. On this route many important and deep results have been found.
Often, modules which carry some extra structure are considered. Thus one considers graded modules, filtered modules, topological modules, modules with a sesquilinear form, etc. (cf. Graded module; Topological module; Filtered module).
References
| [1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) MR0354207 |
| [2] | N. Bourbaki, "Elements of mathematics. Commutative algebra" , Addison-Wesley (1972) (Translated from French) MR0360549 Zbl 0279.13001 |
| [3] | N. Bourbaki, "Elements of mathematics. Lie groups and Lie algebras" , Addison-Wesley (1975) (Translated from French) MR0682756 Zbl 0319.17002 |
| [4] | S. Lang, "Algebra" , Addison-Wesley (1984) MR0783636 Zbl 0712.00001 |
| [5] | B.L. van der Waerden, "Algebra" , 1–2 , Springer (1967–1971) (Translated from German) MR1541390 Zbl 1032.00002 Zbl 1032.00001 Zbl 0903.01009 Zbl 0781.12003 Zbl 0781.12002 Zbl 0724.12002 Zbl 0724.12001 Zbl 0569.01001 Zbl 0534.01001 Zbl 0997.00502 Zbl 0997.00501 Zbl 0316.22001 Zbl 0297.01014 Zbl 0221.12001 Zbl 0192.33002 Zbl 0137.25403 Zbl 0136.24505 Zbl 0087.25903 Zbl 0192.33001 Zbl 0067.00502 |
| [6] | A.I. Kostrikin, "Introduction to algebra" , Springer (1982) (Translated from Russian) MR0661256 Zbl 0482.00001 |
| [7] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) MR0081264 Zbl 0073.02002 |
| [8] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) MR1535024 MR0227205 Zbl 0177.05801 |
| [9] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1981–1976) MR0551052 MR0491784 MR0366960 Zbl 0508.16001 Zbl 0266.16001 |
| [10] | H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956) MR0077480 Zbl 0075.24305 |
| [11] | S. MacLane, "Homology" , Springer (1963) Zbl 0818.18001 Zbl 0328.18009 |
| [12] | H. Bass, "Algebraic 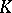 -theory" , Benjamin (1968) MR249491 -theory" , Benjamin (1968) MR249491 |
| [13] | J.W. Milnor, "Introduction to algebraic 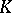 -theory" , Princeton Univ. Press (1971) MR349811 -theory" , Princeton Univ. Press (1971) MR349811 |
Module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Module&oldid=35239