Group
2020 Mathematics Subject Classification: Primary: 20-XX [MSN][ZBL]
One of the main types of algebraic systems (cf. Algebraic system). The theory of groups studies in the most general form properties of algebraic operations which are often encountered in mathematics and their applications; examples of such operations are multiplication of numbers, addition of vectors, successive performance (composition) of transformations, etc. The concept of a group is historically one of the first examples of abstract algebraic systems and served, in many respects, as a model for the restructuring of other mathematical disciplines at the turn into the 20th century, as a result of which the concept of a mathematical system (a structure) has become a fundamental concept in mathematics.
Definition.
A group is a non-empty set with one binary operation that satisfies the following axioms (the operation being written as multiplication):
1) the operation is associative, i.e. (ab)c = a(bc) for any a, b and c in G;
2) the operation admits a unit, i.e. G has an element e, known as the unit element, such that ae=ea=a for any a in G;
3) the operation admits inverse elements, i.e. for any a in G there exists an element x in G, said to be inverse to a, such that ax=xa=e.
The system of axioms 1)–3) is sometimes replaced by an equivalent system of two axioms: 1); and 4) the operation admits left and right quotients, i.e. for any two elements a, b in G there exist elements x, y in G, the left quotient and the right quotient of division of b by a, such that ax=b, and ya=b.
It follows from this definition that the unit element in any group is unique, that the element inverse to any given element in the group is unique and that for any elements a, b of G both fractions obtained by dividing a by b are unique.
Historical remarks.
The origins of the idea of a group are encountered in a number of disciplines, the principal one being the theory of solving algebraic equations by radicals. Permutations were first employed to satisfy the needs of this theory by J.L. Lagrange (1771) in his Memoir on the algebraic solution of equations, and in a paper by A. Vandermonde (1771). It is the former paper which is of special importance in group theory, since it gives, in terms of polynomials, what is really a decomposition of a symmetric permutation group into (right) cosets with respect to subgroups. The deep connections between the properties of permutation groups and those of equations were pointed out by N.H. Abel (1824) and by E. Galois (1830). Galois must be credited with concrete advances in group theory: the discovery of the role played by normal subgroups (cf. Normal subgroup) in problems of solvability of equations by radicals, the discovery that the alternating groups (cf. Alternating group) of order n \ge 5 are simple, etc. C. Jordan's treatise (1870) on permutation groups played an important role in the systematization and development of this branch of algebra.
The idea of a group arose in geometry, in an independent manner, when the only then existing antique geometry had been replaced in the middle of the 19th century by numerous other "geometries" , and finding relations between them had become an urgent problem. This question was solved by studies in projective geometry, which dealt with the behaviour of geometric figures under various transformations. The stress in these studies gradually shifted to the study of the transformations themselves and their classification. Such a "study of geometric mappings" was extensively conducted by A. Möbius, who investigated congruence, similarity, affinity, collineation, and, finally, "elementary types of mappings" of geometric figures, that is, actually, their topological equivalence. A.L. Cayley (1854 and later) and other representatives of the English school of the theory of invariants (cf. Invariants, theory of) gave a more systematic classification of geometries: Cayley explicitly used the term "group" , made systematic use of the multiplication table which now carries his name (cf. Cayley table), proved that any finite group can be represented by permutations, and conceived a group as a system which is defined by its generating elements and defining relations. The final stage in this development was the Erlangen program of F. Klein (1872), who based the classification of geometries on the concept of a transformation group.
Number theory is the third source of the concept of a group. As early as 1761 (cf. Euler function, Primitive root, Series, Stability of an elastic system, Siegel disc, Theta-function, Trigonometric series, Two-term congruence, Variation of constants, Variational calculus, numerical methods of Variational calculus, Venn diagram) L. Euler, in his study of residues remaining in power division, actually used congruences (cf. Congruence) and their division into residue classes, which in group-theoretic language means the decomposition of groups into cosets of subgroups. C.F. Gauss, in his Disquisitiones arithmeticae, studied the cyclotomic equations (cf. Cyclotomic polynomials) and in fact determined subgroups of their Galois groups (cf. Galois group). He also studied the "composition of binary quadratic forms" in this context, and showed, in essence, that the classes of equivalent forms form a finite Abelian group with respect to composition.
Towards the end of the 19th century it was recognized that the group-theoretic ideas employed for a long time in various fields of mathematics were essentially the same, and the modern abstract idea of the concept of a group was finally developed. Thus, as early as 1895, S. Lie defined a group as a set of transformations that is closed under an operation that is associative, admits a unit element and inverse elements. The study of groups without assuming them to be finite and without making any assumptions as to the nature of their elements was first formulated as an independent branch of mathematics with the appearance of the book Abstract group theory by O.Yu. Shmidt (1916).
Examples of groups.
The examples below illustrate the role played by groups in algebra, in other branches of mathematics and in natural sciences.
a) Galois groups. Let K be a finite, separable and normal extension of a field k. The automorphisms of K leaving the elements of k fixed form a group Gal(K/k) with respect to composition, called the Galois group of the extension K/k. The principal theorem in Galois theory states that the mapping which associates to every subgroup of Gal(K/k) its fixed subfield (i.e. the subfield of K whose elements are fixed under the subgroup of Gal(K/k)) is an anti-isomorphism of the lattice of subgroups of Gal(K/k) onto the lattice of intermediate subfields between k and K.
The application to the problem on the solvability of equations by radicals is as follows. Let f be a polynomial in x over k and let K be a splitting field (cf. Splitting field of a polynomial) of f. The group Gal(K/k) is called the Galois group of f over k (its elements are naturally formed by the permutations of the roots of the equation f(x)=0). The result is that the equation f(x)=0 is solvable in radicals if and only if the Galois group of f is solvable (cf. Solvable group).
In this and other similar examples groups appear in the form of automorphism groups (cf. Automorphism) of mathematical structures. This is one of the most important ways of appearance, ensuring groups a special place in algebra. In the words of Galois, automorphisms of arbitrary structures can always be "grouped" , while a ring structure or any other useful structure on a set of automorphisms is successfully introduced in special cases only.
b) Homology groups. The leading idea in homology theory is the application of the theory of (Abelian) groups to the study of a category of topological spaces. To each space X is associated a family of Abelian groups H_0(X),H_1(X),\ldots while each continuous mapping f: X \rightarrow Y defines a family of homomorphisms f_n: H_n(X) \rightarrow H_n(Y), n = 0, 1, \ldots. The study of the homology groups H_n(X) (cf. Homology group) and their homomorphisms by the tools of group theory often makes it possible to deal with a topological problem. A typical example is the extension problem: Is it possible to extend a mapping g: A \rightarrow Y, defined on a subspace A of X, to all of X, i.e. is it possible to represent g as the composite of the imbedding h: A \rightarrow X and some continuous mapping f: X \rightarrow Y? If so, then in the homology spaces one has g_n = f_n h_n, i.e. each homomorphism g_n: H_n(A) \rightarrow H_n(Y) can be factored through H_n(X) with a given homomorphism h_n. If this algebraic problem is unsolvable, then the initial topological problem is unsolvable as well. Important positive results can be obtained in this way.
Homology groups illustrate another typical manner of application of groups: the study of non-algebraic objects by means of algebraic systems which reflect their behaviour. This is in fact the fundamental method of algebraic topology. A similar method, in particular homology groups, is also used with success in the study of algebraic systems themselves — groups, rings, etc. (e.g. in the theory of group extensions).
c) Symmetry groups. The concept of a group makes it possible to describe the symmetries of a given geometrical figure. To any figure one associates the set of spatial transformations that map it onto itself. This set is a group under composition. It also characterizes the symmetry of the figure. This was in fact the approach of E.S. Fedorov (1890) to the problem of classification of regular spatial systems of points, which is one of the basic problems in crystallography (cf. Crystallography, mathematical). There are only 17 plane crystallographic groups (cf. Crystallographic group), which were found directly; there are 230 3-dimensional crystallographic groups, which could be exhaustively classified only by the use of group theory. This is historically the first example of the application of group theory to natural sciences.
Group theory plays a similar role in physics. Thus, the state of a physical system is represented in quantum mechanics by a point in an infinite-dimensional vector space. If the physical system passes from one state into another, its representative point undergoes some linear transformation. The ideas of symmetry and the theory of group representations (cf. Representation of a group) are of prime importance here.
These examples illustrate the contribution of group theory to all classifications where symmetry plays a role. The study of symmetry is actually equivalent to the study of automorphisms of (not necessarily mathematical) systems, and for this reason group theory is indispensable in solving such problems.
Important classes of groups.
The "final objective" of group theory is to describe all group operations or, in other words, all groups, up to isomorphism. Group theory comprises several parts, which are often distinguished by special conditions imposed on the group operation or by the introduction of additional structures into the group, related in some way with the group operation.
The oldest branch of group theory, which is still intensively studied, is the theory of finite groups (cf. Finite group). One of its important tasks is to determine the finite simple groups (cf. Simple finite group). These include many classical groups of matrices over finite fields, and also "sporadic" simple finite groups (Mathieu groups, cf. Mathieu group, etc.). At the other end there are finite solvable groups (cf. Solvable group) in which specific subgroup systems (Hall, Carter, etc., cf. Carter subgroup; Hall subgroup) are usually studied, since these largely determine the structure of the group itself. Finite groups often appear as permutation groups or as matrix groups over finite fields. A large independent branch of the theory of finite groups is the study of representations by matrices and permutations.
A typical method of study of infinite groups is to impose on them some finiteness condition (cf. Group with a finiteness condition). Here, the main interest is centred on periodic groups, locally finite groups, groups with the maximum condition for subgroups (Noetherian groups), groups with the minimum condition for subgroups (Artinian groups), residually-finite groups, groups of finite rank (cf. Rank of a group), and finitely-generated groups (cf. Periodic group; Noetherian group; Artinian group; Residually-finite group; Finitely-generated group).
In the study of Abelian groups (cf. Abelian group) important roles are played by complete Abelian groups, torsion-free Abelian groups and periodic Abelian groups, and inside these groups by pure subgroups and primary subgroups. The study of any given Abelian group is reduced to a large extent to the theories of the classes listed above with the aid of the theory of extensions of Abelian groups, which is mainly developed by homological methods (cf. Extension of a group).
Broader than the class of Abelian groups are the classes of nilpotent groups and of solvable groups (cf. Nilpotent group; Solvable group), the theory of which has also reached a fairly advanced stage. The most useful extensions of nilpotency and solvability are local nilpotency (cf. Locally nilpotent group), local solvability (cf. Locally solvable group) and the normalizer condition, as well as numerous properties determined by the presence of subnormal systems (cf. Subgroup system) of various types in a group. Of importance are special classes of solvable and nilpotent groups: supersolvable groups, polycyclic groups (cf. Supersolvable group; Polycyclic group).
An important branch of group theory is the theory of transformation groups, including permutation groups and the theory of linear groups (cf. Permutation group; Linear group). A number of important classes of groups is defined by the introduction of additional structures compatible with the group operation; this includes topological groups, Lie groups, algebraic groups, and ordered groups (cf. Topological group; Lie group; Algebraic group; Ordered group). Of the other classes of groups, the following are worthy of mention: groups which are free in some variety (cf. Free group), complete groups (cf. Complete group), groups having some property residually (cf. Residually-finite group), groups defined by imposing conditions on their generating elements and defining relations, and groups distinguished by imposing certain conditions on the lattice of subgroups.
References
| [1] | M.I. Kargapolov, J.I. [Yu.I. Merzlyakov] Merzljakov, "Fundamentals of the theory of groups" , Springer (1979) (Translated from Russian) MR0551207 Zbl 0549.20001 |
| [2] | A.G. Kurosh, "The theory of groups" , 1–2 , Chelsea (1955–1956) (Translated from Russian) MR0109842 MR0080089 MR0071422 Zbl 0111.02502 |
| [3] | M. Hall jr., "The theory of groups" , Chelsea, reprint (1976) MR0414669 Zbl 0354.20001 |
| [4] | O.Yu. Shmidt, , Selected works on mathematics , Moscow (1959) pp. 17–70 (In Russian) |
| [5] | H. Wussing, "The genesis of the abstract group concept" , M.I.T. (1984) (Translated from German) MR0746617 Zbl 0547.01001 |
| [6] | E.S. Fedorov, , Symmetry and the structure of crystals. Fundamental works , Moscow (1949) pp. 111–255 (In Russian) |
| [7] | N.N. Bogolyubov, A.A. Logunov, I.T. Todorov, "Introduction to axiomatic quantum field theory" , Benjamin (1975) (Translated from Russian) MR452277 |
Comments
Similar remarks as to the (homotopy) extension problem apply to the (homotopy) lifting problem, in which it is required to fill in a diagram like the one on the right below (the one on the left is the diagram of the extension problem).
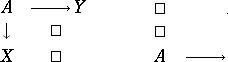 |
An important direction in group theory not mentioned in the article above is combinatorial group theory and the study of group by means of generators and relations [a3], [a4].
Certainly, abstract group theory was considered long before 1916. Thus, W. Burnside, writing in 1897, quotes Cayley as saying that "a group is defined by means of the laws of combination of its symbols" , and goes on to explain why he, in his own book, does, on the whole, not take that point of view; [a5], p. viii. L. Kronecker discussed axioms for abstract finite groups in 1870, cf. [a1] (see also [a10]), and the notion of abstract groups was introduced by Cayley in three papers starting in 1849, [a7]–[a9], though these papers received little attention at the time. This had certainly changed by the 1890's and a discussion of the basic definitions and some basic properties of abstract groups can be found in H. Weber's influential treatise [a6] (1896).
For (a history of) crystallographic groups cf. Crystallographic group.
References
| [a1] | L. Kronecker, "Auseinandersetzung einiger Eigenschaften der Klassenzahl idealer complexer Zahlen" Monatsber. K. Preuss. Akad. Wissenschaft. Berlin (1870) pp. 881–889 ((Also in: Werke, Vol. 1, p. 271)) Zbl 02.0097.01 |
| [a2] | H. Weyl, "Symmetry" , Princeton Univ. Press (1952) (Translated from German) MR0048449 Zbl 0046.00406 |
| [a3] | W. Magnus, A. Karrass, B. Solitar, "Combinatorial group theory: presentations in terms of generators and relations" , Wiley (Interscience) (1966) pp. 412 Zbl 0138.25604 |
| [a4] | H.S.M. Coxeter, W.O.J. Moser, "Generators and relations for discrete groups" , Springer (1957) MR0088489 Zbl 0077.02801 |
| [a5] | W. Burnside, "Theory of groups of finite order" , Dover, reprint (1955) (Translated from German) MR0069818 Zbl 0064.25105 |
| [a6] | H. Weber, "Lehrbuch der Algebra" , II , Vieweg (1899) pp. Buch 1, Abschnitt 1 Zbl 30.0093.01 |
| [a7] | A. Cayley, "Note on the theory of permutations" Phil. Mag. (3) , 34 (1849) pp. 527–529 ((Also in: Collected mathematical papers, Vol. I, 432–424)) |
| [a8] | A. Cayley, "On the theory of groups as depending on the symbolical equation \theta^n=1" Phil. Mag. (4) , 7 (1854) pp. 40–47 ((Also in: Collected mathematical papers, Vol. II, 123–130)) |
| [a9] | A. Cayley, "On the theory of groups as depending on the symbolical equation \theta^n=1. Second part" Phil. Mag. (4) , 7 (1854) pp. 408–409 ((Also in: Collected mathematical papers, Vol. II, 131–132)) |
| [a10] | G.F. Frobenius, "Neuer Beweis des Sylowschen Satzes" J. Reine Angew. Math. , 100 (1887) pp. 179–181 |
Group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Group&oldid=39401