Functional analysis
The part of modern mathematical analysis in which the basic purpose is to study functions 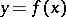 for which at least one of the variables
for which at least one of the variables  or
or 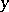 varies over an infinite-dimensional space. In its most general form such a study falls into three parts: 1) the introduction and study of infinite-dimensional spaces as such; 2) the study of the simplest functions, namely, when
varies over an infinite-dimensional space. In its most general form such a study falls into three parts: 1) the introduction and study of infinite-dimensional spaces as such; 2) the study of the simplest functions, namely, when  takes values in an infinite-dimensional space and
takes values in an infinite-dimensional space and 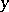 in a one-dimensional space (these are called functionals (cf. Functional), whence the name "functional analysis" ); and 3) the study of general functions of the type indicated — operators (cf. Operator). Linear functions
in a one-dimensional space (these are called functionals (cf. Functional), whence the name "functional analysis" ); and 3) the study of general functions of the type indicated — operators (cf. Operator). Linear functions 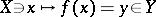 , i.e. linear operators, have been most completely studied. Their theory is essentially a generalization of linear algebra to the infinite-dimensional case. A combination of the approaches of classical analysis and algebra is characteristic for the methods of functional analysis, and this leads to relations between what are at first glance very distant branches of mathematics.
, i.e. linear operators, have been most completely studied. Their theory is essentially a generalization of linear algebra to the infinite-dimensional case. A combination of the approaches of classical analysis and algebra is characteristic for the methods of functional analysis, and this leads to relations between what are at first glance very distant branches of mathematics.
Functional analysis as an independent mathematical discipline started at the turn of the 19th century and was finally established in the 1920's and 1930's, on the one hand under the influence of the study of specific classes of linear operators — integral operators and integral equations connected with them — and on the other hand under the influence of the purely intrinsic development of modern mathematics with its desire to generalize and thus to clarify the true nature of some regular behaviour. Quantum mechanics also had a great influence on the development of functional analysis, since its basic concepts, for example energy, turned out to be linear operators (which physicists at first rather loosely interpreted as infinite-dimensional matrices) on infinite-dimensional spaces.
1. The concept of a space.
Topological vector spaces (cf. Topological vector space) are the most general spaces figuring in functional analysis. These are vector (linear) spaces 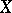 over the field of complex numbers
over the field of complex numbers 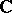 (or any other field, for example that of the real numbers,
(or any other field, for example that of the real numbers, 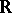 ) which are simultaneously topological spaces and where the linear structure and the topology are compatible in the sense that the linear operations are continuous in the topology under consideration. In particular, if
) which are simultaneously topological spaces and where the linear structure and the topology are compatible in the sense that the linear operations are continuous in the topology under consideration. In particular, if 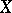 is a metric space, then one has a metric vector space.
is a metric space, then one has a metric vector space.
A more particular, but very important, situation arises when the concept of the norm 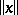 (the length) of a vector
(the length) of a vector 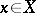 is introduced axiomatically in a vector space
is introduced axiomatically in a vector space 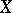 . A vector space with a norm is called a normed space. It is metrizable. A metric
. A vector space with a norm is called a normed space. It is metrizable. A metric 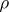 is introduced by the formula:
is introduced by the formula: 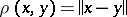 . A vector space with a norm is called a Banach space if it is complete with respect to the metric indicated.
. A vector space with a norm is called a Banach space if it is complete with respect to the metric indicated.
In a large number of problems the situation arises where one can introduce an inner product 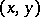 for any two vectors in the vector space
for any two vectors in the vector space  , such that this product generalizes the usual scalar product in three-dimensional space. A space provided with an inner product is called a pre-Hilbert space; it is a particular case of a normed space. If this space is complete, then it is called a Hilbert space.
, such that this product generalizes the usual scalar product in three-dimensional space. A space provided with an inner product is called a pre-Hilbert space; it is a particular case of a normed space. If this space is complete, then it is called a Hilbert space.
Infinite-dimensional spaces are studied in functional analysis, that is, spaces in which there is an infinite set of linearly independent vectors.
From a geometric point of view the simplest spaces are the Hilbert spaces  , which have properties that mostly resemble those of finite-dimensional spaces, because it is possible to introduce a concept similar to that of the angle between two vectors by means of the inner product. In particular, two vectors
, which have properties that mostly resemble those of finite-dimensional spaces, because it is possible to introduce a concept similar to that of the angle between two vectors by means of the inner product. In particular, two vectors  are said to be orthogonal
are said to be orthogonal 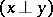 if
if 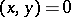 . The following result is true in
. The following result is true in 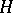 : Let
: Let 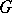 be a subspace of
be a subspace of 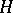 , then any vector
, then any vector 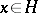 has a projection
has a projection 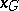 onto
onto 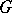 , that is, a vector
, that is, a vector 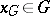 such that
such that 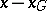 is orthogonal to any vector in
is orthogonal to any vector in 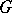 . Due to this fact, a large number of geometric constructions which hold for finite-dimensional spaces can be transferred to Hilbert spaces, where they often acquire an analytic character.
. Due to this fact, a large number of geometric constructions which hold for finite-dimensional spaces can be transferred to Hilbert spaces, where they often acquire an analytic character.
Geometric questions become distinctly more complicated when going from Hilbert spaces to Banach spaces, and all the more so in general topological vector spaces, because orthogonal projection is not meaningful in them. For example, in the space 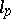 (
(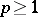 ) the vectors
) the vectors 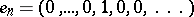 form a basis in the sense that for each vector
form a basis in the sense that for each vector 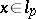 "coordinate-wise" expansion is valid:
"coordinate-wise" expansion is valid:
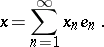 |
The construction of a basis for the space 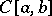 is already a bit more complicated; at the same time a basis can be constructed in each of the known examples of Banach spaces. The problem arose: Does there exist a basis in every Banach space? This problem, in spite of the efforts of many mathematicians, did not yield a solution for more than 40 years and was only solved negatively in 1972 (see [23]). In functional analysis an important place is occupied by "geometric" themes, devoted to clarifying the properties of various sets in Banach and other spaces, for example convex sets, compact sets (the latter means that every sequence of points of such a set
is already a bit more complicated; at the same time a basis can be constructed in each of the known examples of Banach spaces. The problem arose: Does there exist a basis in every Banach space? This problem, in spite of the efforts of many mathematicians, did not yield a solution for more than 40 years and was only solved negatively in 1972 (see [23]). In functional analysis an important place is occupied by "geometric" themes, devoted to clarifying the properties of various sets in Banach and other spaces, for example convex sets, compact sets (the latter means that every sequence of points of such a set 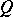 has a subsequence converging to a point in
has a subsequence converging to a point in 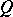 ), etc. Here, simply formulated questions often have very non-trivial solutions. These problems are closely connected with the study of isomorphisms between spaces, and with finding universal representatives in some classes of spaces.
), etc. Here, simply formulated questions often have very non-trivial solutions. These problems are closely connected with the study of isomorphisms between spaces, and with finding universal representatives in some classes of spaces.
Specific function spaces have been studied in detail, since the properties of these spaces usually determine the character of the solution to a problem when it is obtained by the methods of functional analysis. The so-called imbedding theorems for the Sobolev spaces 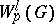 ,
, 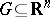 , and various generalizations of these, can serve as an example.
, and various generalizations of these, can serve as an example.
In connection with the demands of modern mathematical physics a great number of specific spaces have arisen in which problems are naturally posed and which thus must be studied. These spaces are usually constructed from initial spaces using certain constructions. Below the most commonly used constructions are given in their simplest versions.
1) The formation of an orthogonal sum 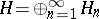 of Hilbert spaces
of Hilbert spaces 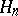 ,
, 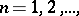 is a construction of a space
is a construction of a space 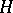 in terms of spaces
in terms of spaces 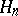 , similar to the formation of
, similar to the formation of 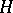 in terms of one-dimensional spaces.
in terms of one-dimensional spaces.
2) Passing to a quotient space: Given a degenerate inner product 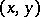 in a vector space
in a vector space 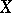 (that is,
(that is, 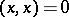 is possible when
is possible when 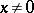 ); the Hilbert space
); the Hilbert space 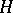 is defined as the completion of
is defined as the completion of 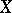 with respect to
with respect to 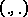 after first identifying with 0 all those vectors for which
after first identifying with 0 all those vectors for which 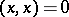 .
.
3) The formation of a tensor product 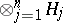 is analogous to passing from functions of one variable
is analogous to passing from functions of one variable 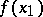 to functions of several variables
to functions of several variables 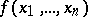 ; a similar construction is also used for an infinite number of factors; one also considers symmetric and anti-symmetric tensor products consisting, in the case of functions, of functions of several variables having these properties.
; a similar construction is also used for an infinite number of factors; one also considers symmetric and anti-symmetric tensor products consisting, in the case of functions, of functions of several variables having these properties.
4) The formation of the projective limit 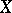 of Banach spaces
of Banach spaces 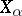 , where
, where 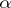 runs over a certain set of indices
runs over a certain set of indices 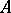 . By definition,
. By definition, 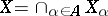 ; the topology in
; the topology in 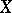 , roughly speaking, is given by the convergence
, roughly speaking, is given by the convergence 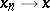 which means that
which means that  with respect to the norm in every
with respect to the norm in every 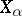 .
.
5) The formation of the inductive limit 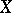 of the Banach spaces
of the Banach spaces 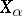 . By definition,
. By definition, 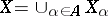 ; the topology in
; the topology in 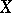 , roughly speaking, is given by the convergence
, roughly speaking, is given by the convergence  which means that all the
which means that all the 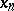 lie in a certain
lie in a certain 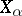 and that
and that 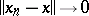 with respect to the norm of this space.
with respect to the norm of this space.
6) Interpolation is the formation of "intermediate" spaces 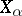 from two spaces
from two spaces 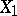 and
and 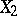 , where
, where 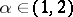 ; for example, the construction from
; for example, the construction from 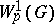 and
and 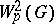 of the space
of the space 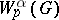 of functions with fractional derivative
of functions with fractional derivative 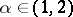 .
.
Procedures 4) and 5) are commonly applied when constructing topological vector spaces. One distinguishes among such spaces the very important class of the so-called nuclear spaces (cf. Nuclear space), each of which is constructed as a projective limit of Hilbert spaces 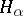 with the property that, for each
with the property that, for each 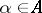 , one can find a
, one can find a 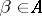 such that
such that 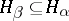 and the imbedding operator
and the imbedding operator 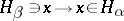 is a Hilbert–Schmidt operator (see below, Section
is a Hilbert–Schmidt operator (see below, Section  ).
).
An extensive and important branch of functional analysis has been developed in which one studies topological and normed vector spaces with a partial order, introduced axiomatically, having natural properties (partially ordered spaces).
2. Functionals.
In functional analysis the study of continuous functionals and linear functionals plays an essential role (cf. Continuous functional; Linear functional); their properties are closely connected with the properties of the original space 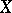 .
.
Let 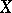 be a Banach space and let
be a Banach space and let 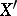 be the set of continuous linear functionals on it;
be the set of continuous linear functionals on it; 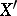 is a vector space with respect to the usual operations of adding functions and multiplying them by a number, it becomes a Banach space if one introduces the norm
is a vector space with respect to the usual operations of adding functions and multiplying them by a number, it becomes a Banach space if one introduces the norm
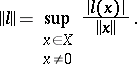 |
The space  is called the dual of
is called the dual of 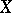 (cf. also Adjoint space).
(cf. also Adjoint space).
If  is finite-dimensional, then every linear functional is of the form
is finite-dimensional, then every linear functional is of the form
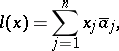 |
where 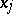 are the coordinates of the vector
are the coordinates of the vector  with respect to a certain basis and
with respect to a certain basis and 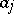 are numbers determined by the functional. It turns out that the formula also holds when
are numbers determined by the functional. It turns out that the formula also holds when 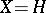 is a Hilbert space (Riesz' theorem). Namely, in this case
is a Hilbert space (Riesz' theorem). Namely, in this case 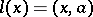 , where
, where  is a certain vector in
is a certain vector in 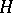 . This formula shows that a Hilbert space essentially coincides with its dual.
. This formula shows that a Hilbert space essentially coincides with its dual.
For a Banach space the situation is far more complicated: One can construct 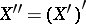 ,
, 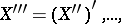 and these spaces may turn out to be all different. At the same time, there always exists a canonical imbedding of
and these spaces may turn out to be all different. At the same time, there always exists a canonical imbedding of 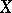 into
into 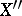 , namely, to each
, namely, to each 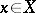 one can associate the functional
one can associate the functional 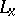 , where
, where 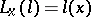 ,
, 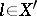 . The spaces
. The spaces 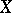 for which
for which 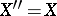 are called reflexive. Generally, in the case of a Banach space even the existence of non-trivial (that is, non-zero) linear functionals is not a simple question. This question is easily solved affirmatively with the help of the Hahn–Banach theorem.
are called reflexive. Generally, in the case of a Banach space even the existence of non-trivial (that is, non-zero) linear functionals is not a simple question. This question is easily solved affirmatively with the help of the Hahn–Banach theorem.
The dual space 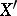 is, in a certain sense, "better" than the original space
is, in a certain sense, "better" than the original space 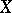 . For example, along with the norm one can introduce another (weak) topology in
. For example, along with the norm one can introduce another (weak) topology in 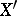 which, in terms of convergence, is such that
which, in terms of convergence, is such that 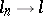 if
if 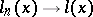 for all
for all  . In this topology the unit ball in
. In this topology the unit ball in 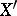 is compact (which is never the case for infinite-dimensional spaces in the topology generated by a norm). This makes it possible to study in more detail a number of geometric questions about sets in the dual space (for example, establishing the structure of convex sets, etc.).
is compact (which is never the case for infinite-dimensional spaces in the topology generated by a norm). This makes it possible to study in more detail a number of geometric questions about sets in the dual space (for example, establishing the structure of convex sets, etc.).
For a number of specific spaces 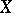 the dual space
the dual space 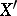 can be found explicitly. However, for the majority of Banach spaces, and especially for topological vector spaces, the functionals are elements of a new kind which cannot be expressed simply in terms of classical analysis. The elements of the dual space are called generalized functions.
can be found explicitly. However, for the majority of Banach spaces, and especially for topological vector spaces, the functionals are elements of a new kind which cannot be expressed simply in terms of classical analysis. The elements of the dual space are called generalized functions.
For many questions in functional analysis and its applications an essential role is played by a triple of spaces 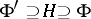 , where
, where 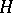 is the original Hilbert space,
is the original Hilbert space, 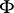 is a topological vector space (in particular, a Hilbert space with a different inner product) and
is a topological vector space (in particular, a Hilbert space with a different inner product) and 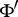 is its dual space, the elements of which can be taken as generalized functions. The space
is its dual space, the elements of which can be taken as generalized functions. The space 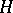 itself is then called a rigged Hilbert space.
itself is then called a rigged Hilbert space.
The study of linear functionals on 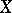 in many respects promotes a deeper understanding of the nature of the original space
in many respects promotes a deeper understanding of the nature of the original space 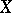 . On the other hand, in many questions it is necessary to study general functions
. On the other hand, in many questions it is necessary to study general functions 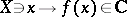 , that is, non-linear functionals in the case of an infinite-dimensional
, that is, non-linear functionals in the case of an infinite-dimensional 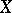 (cf. Non-linear functional). Since the unit ball in such a space
(cf. Non-linear functional). Since the unit ball in such a space 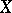 is non-compact, its study often encounters essential difficulties, although, for example, such concepts as the differentiability of
is non-compact, its study often encounters essential difficulties, although, for example, such concepts as the differentiability of 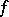 , its analyticity, etc. are easily generalized. One can consider a set of functions
, its analyticity, etc. are easily generalized. One can consider a set of functions 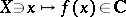 having definite properties as a new topological vector space of functions of "an infinite number of variables" . Such functions also appear in constructing infinite tensor products
having definite properties as a new topological vector space of functions of "an infinite number of variables" . Such functions also appear in constructing infinite tensor products 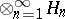 of spaces of functions of one variable. The study of such spaces, of the operators on them, etc., is connected with the requirements of quantum field theory (see [22]).
of spaces of functions of one variable. The study of such spaces, of the operators on them, etc., is connected with the requirements of quantum field theory (see [22]).
3. Operators.
The main objects of study in functional analysis are operators 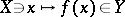 , where
, where 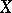 and
and 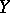 are topological vector (for the most part, normed or Hilbert) spaces and, above all, linear operators (cf. Linear operator).
are topological vector (for the most part, normed or Hilbert) spaces and, above all, linear operators (cf. Linear operator).
When 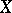 and
and 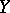 are finite-dimensional, the linearity of an operator implies that it is of the form
are finite-dimensional, the linearity of an operator implies that it is of the form
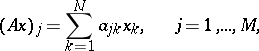 |
where 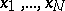 are the coordinates of the vector
are the coordinates of the vector  in a certain basis, and
in a certain basis, and 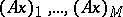 are, analogously, the coordinates of
are, analogously, the coordinates of 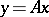 . Thus, in the finite-dimensional case to each linear operator
. Thus, in the finite-dimensional case to each linear operator 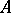 corresponds, in terms of fixed bases in
corresponds, in terms of fixed bases in 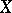 and
and 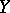 , a matrix
, a matrix
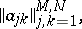 |
which gives a simple expression for 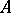 . The study of linear operators in this case is a topic of linear algebra.
. The study of linear operators in this case is a topic of linear algebra.
The situation becomes much more complicated when 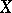 and
and 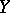 become infinite-dimensional (even Hilbert) spaces. First of all, two classes of operators arise here: continuous operators, for which the function
become infinite-dimensional (even Hilbert) spaces. First of all, two classes of operators arise here: continuous operators, for which the function 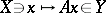 is continuous (they are also called bounded, since the continuity of an operator between Banach spaces is equivalent to its boundedness), and unbounded operators, where there is no such continuity. The operators of the first type are simpler, but those of the second type are met more often, e.g. differential operators are of the second type.
is continuous (they are also called bounded, since the continuity of an operator between Banach spaces is equivalent to its boundedness), and unbounded operators, where there is no such continuity. The operators of the first type are simpler, but those of the second type are met more often, e.g. differential operators are of the second type.
The important (especially for quantum mechanics) class of self-adjoint operators on a Hilbert space 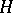 has been studied most of all (cf. Self-adjoint operator).
has been studied most of all (cf. Self-adjoint operator).
Other classes of operators on 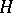 , closely connected with the self-adjoint operators (the so-called unitary and normal operators, cf. Unitary operator; Normal operator), have also been well studied.
, closely connected with the self-adjoint operators (the so-called unitary and normal operators, cf. Unitary operator; Normal operator), have also been well studied.
Among the general facts about bounded operators acting in a Banach space 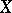 , one can select the construction of a functional calculus of analytic functions. Namely, the operator
, one can select the construction of a functional calculus of analytic functions. Namely, the operator 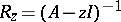 is called the resolvent of the operator
is called the resolvent of the operator 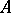 , where
, where 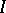 is the identity operator and
is the identity operator and 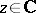 . The points
. The points  for which the inverse operator
for which the inverse operator 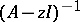 exists are called the regular points of
exists are called the regular points of 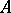 , the complement of the set of regular points is called the spectrum
, the complement of the set of regular points is called the spectrum 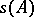 of
of 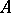 . The spectrum is never empty and lies in the disc
. The spectrum is never empty and lies in the disc 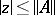 ; the eigen values of
; the eigen values of 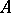 , of course, belong to
, of course, belong to 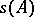 , but the spectrum, generally speaking, does not entirely consist of them. If
, but the spectrum, generally speaking, does not entirely consist of them. If 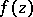 is an analytic function defined in a neighbourhood of
is an analytic function defined in a neighbourhood of 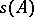 , and if
, and if 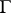 is some closed contour enclosing
is some closed contour enclosing 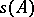 and lying in the domain of analyticity of
and lying in the domain of analyticity of 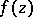 , then one puts
, then one puts
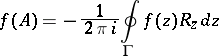 |
and calls 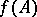 an operator function. If
an operator function. If 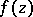 is a polynomial, then
is a polynomial, then 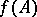 is obtained by simply replacing
is obtained by simply replacing  in this polynomial by
in this polynomial by 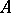 . The correspondence
. The correspondence 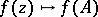 has the important homomorphism properties:
has the important homomorphism properties:
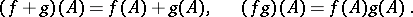 |
Thus, under definite conditions on 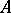 one can define, for example,
one can define, for example, 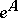 ,
, 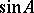 ,
, 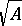 , etc.
, etc.
Among the special classes of operators acting on a Banach space 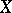 the most important role is played by the so-called completely-continuous or compact operators (cf. Completely-continuous operator; Compact operator). If
the most important role is played by the so-called completely-continuous or compact operators (cf. Completely-continuous operator; Compact operator). If 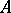 is compact, then the equation
is compact, then the equation 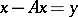 (
(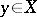 is a given vector and
is a given vector and 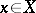 is the desired vector) has been well studied. The analogues of all the facts which hold for linear equations in finite-dimensional spaces are also valid for this equation (the so-called Fredholm theory). For compact operators
is the desired vector) has been well studied. The analogues of all the facts which hold for linear equations in finite-dimensional spaces are also valid for this equation (the so-called Fredholm theory). For compact operators 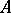 one studies conditions which ensure that the system of eigen vectors of
one studies conditions which ensure that the system of eigen vectors of 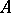 and their associated vectors are dense in
and their associated vectors are dense in 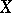 , that is, any vector in
, that is, any vector in 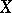 can be approximated by linear combinations of eigen vectors and associated vectors; etc. At the same time there are, even for compact operators, problems which naturally arise but which are very difficult to solve (for example, the theorem that each such operator has an invariant subspace
can be approximated by linear combinations of eigen vectors and associated vectors; etc. At the same time there are, even for compact operators, problems which naturally arise but which are very difficult to solve (for example, the theorem that each such operator has an invariant subspace 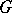 different from 0 and the whole of
different from 0 and the whole of 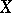 , that is, a subspace
, that is, a subspace 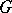 such that
such that 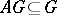 ; in the finite-dimensional case the existence of
; in the finite-dimensional case the existence of 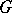 follows trivially from the fact that the spectrum is non-empty).
follows trivially from the fact that the spectrum is non-empty).
The spectrum of a compact operator 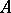 is discrete and may accumulate at 0 only. One distinguishes important subclasses of the class of compact operators according to the rate at which the eigen values approach 0. Thus, very often one encounters Hilbert–Schmidt operators. If
is discrete and may accumulate at 0 only. One distinguishes important subclasses of the class of compact operators according to the rate at which the eigen values approach 0. Thus, very often one encounters Hilbert–Schmidt operators. If 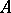 is an operator on
is an operator on 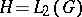 , then it is a Hilbert–Schmidt operator if and only if it is an integral operator with kernel
, then it is a Hilbert–Schmidt operator if and only if it is an integral operator with kernel 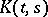 that is square-summable in both variables. Compact Volterra operators have also been studied in detail. A study has also been made of spectral operators for which there is an analogue for the resolution of the identity
that is square-summable in both variables. Compact Volterra operators have also been studied in detail. A study has also been made of spectral operators for which there is an analogue for the resolution of the identity 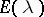 ; etc. (see [8]).
; etc. (see [8]).
4. Banach algebras and representation theory.
In the early stages of the development of functional analysis the problems studied were those that could be stated and solved in terms of linear operations on elements of the space alone.
One of the powerful methods in mathematics is to represent abstract mathematical objects by simpler (or more concrete) objects. For example, the spectral theorem can be interpretated as representing a self-adjoint operator by the operator which multiplies the measurable functions of a certain class by the independent variable. If one considers multiplication by Borel functions, one obtains a representation of a commutative normed algebra of operators on a Hilbert space. A more general example of this representation gives one of the main theorems in the theory of commutative Banach algebras.
Let 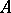 be a commutative Banach algebra, for simplicity with an identity, that is, a Banach space in which there is a commutative and associative multiplication
be a commutative Banach algebra, for simplicity with an identity, that is, a Banach space in which there is a commutative and associative multiplication 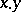 of elements
of elements 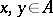 , and let the norm satisfy
, and let the norm satisfy 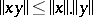 . Further, let
. Further, let 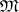 be the set of all maximal ideals. Then a compact topology can be introduced on
be the set of all maximal ideals. Then a compact topology can be introduced on 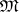 so that every element
so that every element 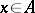 represents a complex-valued continuous function
represents a complex-valued continuous function 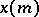 ,
, 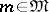 , and, moreover, the sum
, and, moreover, the sum 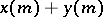 and the product
and the product 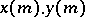 of functions correspond to the sum
of functions correspond to the sum 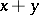 and the product
and the product 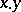 , respectively (see [7]). In the non-commutative case representation theory has been studied especially for the so-called algebras with an involution (see Banach algebra).
, respectively (see [7]). In the non-commutative case representation theory has been studied especially for the so-called algebras with an involution (see Banach algebra).
A considerably richer representation theory has been developed for topological groups (cf. Representation of a topological group).
5. Non-linear functional analysis.
At the same time as the concept of a space was being developed and deepened, the concept of a function was being developed and generalized. In the end it became necessary to consider mappings (not necessarily linear) from one space into another. One of the central problems in non-linear functional analysis is the study of such mappings. As in the linear case, a mapping of a space into (the real or complex) numbers is called a functional. For non-linear mappings (in particular, non-linear functionals) there are various methods to define the concepts of a differential, a directional derivative, etc., analogous to the corresponding concepts in classical mathematical analysis (see [11], [13], [15] and Differentiation of a mapping).
An important problem in non-linear functional analysis is the problem of determining the fixed points of a mapping (see [11], [13], [15] and Fixed point).
When studying the eigen vectors of a non-linear mapping containing a parameter there arises a phenomenon that is crucial in non-linear analysis — so-called bifurcation (see [15]).
In the investigation of fixed points and bifurcation points, topological methods are extensively used: the generalization to infinite-dimensional spaces of the Brouwer–Bohl theorem on the existence of fixed points for mappings of finite-dimensional spaces, the index of a mapping (cf. Index formulas), etc.
6. The application of functional analysis in mathematical and theoretical physics.
Below, those branches of mathematical physics are given in which some part of functional analysis is applied.
1) The spectral theory of operators is applied in all theories of quantum physics: in quantum  -body theory, in quantum field theory and in quantum statistical mechanics. In addition, spectral theory is applied in the study of models of dynamical systems in classical mechanics, in the study of linearized equations in hydrodynamics, in the study of Gibbs fields, etc.
-body theory, in quantum field theory and in quantum statistical mechanics. In addition, spectral theory is applied in the study of models of dynamical systems in classical mechanics, in the study of linearized equations in hydrodynamics, in the study of Gibbs fields, etc.
2) Scattering theory is applied in quantum physics. It should be noted that the modern mathematical theory of scattering arose first of all in physics. In recent years scattering theory (the inverse problem) has often been applied in integrating non-linear model equations in mathematical physics.
3) Banach algebras are applied in quantum field theory, especially in so-called axiomatic field theory, and in studying various integrable models of a quantum field and statistical mechanics. Von Neumann algebras are also used in these questions.
4) Perturbation theory, mainly the perturbation theory for linear operators, is applied in almost-all domains of mathematical physics: in quantum field theory and in statistical mechanics, both equilibrium and non-equilibrium (especially in investigating the so-called kinetic equations, the compound spectra of multi-particle systems, etc.).
5) Functional integration and measures in function spaces are applied in constructive quantum field theory and in quantum statistical mechanics.
6) Various integral representations (Riesz' theorem, the Krein–Mil'man theorem, Choquet's theorem, and others) are applied in axiomatic quantum field theory and in statistical mechanics.
7) Vector spaces (mainly Hilbert spaces) are applied in quantum theory and in statistical physics.
8) Generalized functions are applied everywhere in mathematical physics as an important analytic tool (see also Generalized function).
References
| [1] | N.I. [N.I. Akhiezer] Ahiezer, "Theory of linear operators in Hilbert space" , 1–2 , Pitman (1984) (Translated from Russian) MR0509335 MR0486990 MR0206710 MR0264421 MR0264420 MR0044034 |
| [2] | S.S. Banach, "A course of functional analysis" , Kiev (1948) (In Ukrainian) |
| [3] | Yu.M. [Yu.M. Berezanskii] Berezanskiy, "Expansion in eigenfunctions of selfadjoint operators" , Amer. Math. Soc. (1968) (Translated from Russian) |
| [4] | N. Bourbaki, "Elements of mathematics. Topological vector spaces" , Springer (1987) (Translated from French) MR0928386 Zbl 0622.46001 |
| [5] | B.Z. Vulikh, "Introduction to the theory of partially ordered spaces" , Wolters-Noordhoff (1967) (Translated from Russian) MR0224522 Zbl 0186.44601 |
| [6] | I.M. Gel'fand, G.E. Shilov, "Generalized functions" , Acad. Press (1964) (Translated from Russian) MR435831 Zbl 0115.33101 |
| [7] | I.M. [I.M. Gel'fand] Gelfand, D.A. [D.A. Raikov] Raikov, G.E. [G.E. Shilov] Schilow, "Kommutative Normierte Ringe" , Deutsch. Verlag Wissenschaft. (1964) (Translated from Russian) |
| [8] | N. Dunford, J.T. Schwartz, "Linear operators" , 1–3 , Interscience (1958–1971) MR1009164 MR1009163 MR1009162 MR0412888 MR0216304 MR0188745 MR0216303 MR1530651 MR0117523 Zbl 0635.47003 Zbl 0635.47002 Zbl 0635.47001 Zbl 0283.47002 Zbl 0243.47001 Zbl 0146.12601 Zbl 0128.34803 Zbl 0084.10402 |
| [9] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 MR0617913 Zbl 0435.46002 |
| [10] | L.V. Kantorovich, "Functional analysis and applied mathematics" Uspekhi Mat. Nauk , 3 : 6 (1948) pp. 89–185 (In Russian) MR0053389 Zbl 0034.21203 |
| [11] | L.V. Kantorovich, G.P. Akilov, "Functionalanalysis in normierten Räumen" , Akademie Verlag (1964) (Translated from Russian) |
| [12] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) MR0412321 Zbl 0342.22001 |
| [13] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) MR1025126 MR0708717 MR0630899 MR0435771 MR0377444 MR0234241 MR0215962 MR0118796 MR1530727 MR0118795 MR0085462 MR0070045 Zbl 0932.46001 Zbl 0672.46001 Zbl 0501.46001 Zbl 0501.46002 Zbl 0235.46001 Zbl 0103.08801 |
| [14] | M.A. Krasnosel'skii, "Topological methods in the theory of nonlinear integral equations" , Pergamon (1964) (Translated from Russian) Zbl 0111.30303 |
| [15] | W.I. [V.I. Sobolev] Sobolew, "Elemente der Funktionalanalysis" , H. Deutsch , Frankfurt a.M. (1979) (Translated from Russian) MR0539144 Zbl 0338.46011 Zbl 0325.46017 Zbl 0159.17601 Zbl 0090.32302 Zbl 0064.10501 |
| [16] | M.A. Naimark, "Linear differential operators" , 1–2 , F. Ungar (1967–1968) (Translated from Russian) MR2814127 MR0353061 MR0262880 MR0216050 MR0067292 MR0050109 Zbl 1221.47085 Zbl 0227.34020 Zbl 0219.34001 Zbl 0057.07102 |
| [17] | M.A. Naimark, "Normed rings" , Reidel (1984) (Translated from Russian) MR1292007 MR0355601 MR0355602 MR0205093 MR0110956 MR0090786 MR0026763 Zbl 0218.46042 Zbl 0137.31703 Zbl 0089.10102 Zbl 0073.08902 |
| [18] | M. Reed, B. Simon, "Methods of modern mathematical physics" , 1–4 , Acad. Press (1972–1978) MR0751959 MR0529429 MR0493423 MR0493421 MR0493422 MR0493420 MR0493419 Zbl 0521.47001 Zbl 0517.47006 Zbl 0459.46001 Zbl 0405.47007 Zbl 0401.47001 Zbl 0308.47002 Zbl 0242.46001 |
| [19] | F. Riesz, B. Szökefalvi-Nagy, "Functional analysis" , F. Ungar (1955) (Translated from French) MR0071727 Zbl 0732.47001 Zbl 0070.10902 Zbl 0046.33103 |
| [20] | S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) MR0165337 Zbl 0123.09003 |
| [21] | E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) MR0089373 Zbl 0392.46001 Zbl 0033.06501 |
| [22] | A.S. Švarc, "Mathematical foundations of quantum field theory" , Moscow (1975) (In Russian) MR0468857 |
| [23] | P. Enflö, "A counterexample to the approximation problem in Banach spaces" Acta. Math. , 130 (1973) pp. 309–317 MR0402468 |
Comments
References
| [a1] | W. Rudin, "Functional analysis" , McGraw-Hill (1973) MR0365062 Zbl 0253.46001 |
| [a2] | J.B. Conway, "A course in functional analysis" , Springer (1985) MR0768926 Zbl 0558.46001 |
| [a3] | H.H. Schaefer, "Topological vector spaces" , Macmillan (1966) MR0193469 Zbl 0141.30503 |
| [a4] | S.S. Banach, "Théorie des opérations linéaires" , Hafner (1932) MR1357166 MR0389498 MR0071726 Zbl 0005.20901 Zbl 58.0420.01 |
| [a5] | G. Köthe, "Topological vector spaces" , I-II , Springer (1979) MR0551623 Zbl 0417.46001 |
| [a6] | J. Lindenstrauss, L. Tzafriri, "Classical Banach spaces" , 1–2 , Springer (1977–1979) MR0540367 MR0500056 MR0415253 MR0425583 MR0291772 Zbl 0852.46015 Zbl 0403.46022 Zbl 0362.46013 Zbl 0259.46011 Zbl 0224.46041 Zbl 0224.46032 |
| [a7] | H.H. Schaefer, "Banach lattices and positive operators" , Springer (1974) MR0423039 Zbl 0296.47023 |
| [a8] | J. Horvath, "Topological vector spaces and distributions" , Addison-Wesley (1966) MR0205028 Zbl 0143.15101 |
| [a9] | A. Grothendieck, "Résumé de la théorie métrique des produits tensoriels topologiques" Bol. Soc. Mat. São Paulo , 8 (1956) pp. 1–79 MR1466414 MR0094682 Zbl 0074.32303 |
| [a10] | A. Pietsch, "Operator ideals" , North-Holland (1980) MR0600820 MR0583295 MR0592903 MR0582655 Zbl 0455.47032 Zbl 0441.47032 Zbl 0434.47030 |
| [a11] | J. Diestel, J.J. Uhl jr., "Vector measures" , Math. Surveys , 15 , Amer. Math. Soc. (1977) MR0453964 Zbl 0369.46039 |
| [a12] | R.V. Kadison, J.R. Ringrose, "Fundamentals of the theory of operator algebras" , 1–2 , Acad. Press (1983–1986) MR1468230 MR1468229 MR1170351 MR1134132 MR0859186 MR0719020 Zbl 0991.46031 Zbl 0888.46039 Zbl 0831.46060 Zbl 0869.46029 Zbl 0869.46028 Zbl 0601.46054 Zbl 0518.46046 |
| [a13] | T. Kato, "Perturbation theory for linear operators" , Springer (1976) MR0407617 Zbl 0342.47009 |
| [a14] | J.T. Schwartz, "Non-linear functional analysis" , Gordon & Breach (1969) |
| [a15] | G. Choquet, "Lectures on analysis" , 1–3 , Benjamin (1969) (Translated from French) MR0250013 MR0250012 MR0250011 Zbl 0181.39603 Zbl 0181.39602 Zbl 0181.39601 |
| [a16] | C.E. Rickart, "General theory of Banach algebras" , v. Nostrand (1960) MR0115101 Zbl 0095.09702 |
| [a17] | W.A.J. Luxemburg, A.C. Zaanen, "Riesz spaces" , I , North-Holland (1971) MR0511676 Zbl 0231.46014 |
| [a18] | L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1950–1951) MR2067351 MR0209834 MR0117544 MR0107812 MR0041345 MR0035918 MR0032815 MR0031106 MR0025615 Zbl 0962.46025 Zbl 0653.46037 Zbl 0399.46028 Zbl 0149.09501 Zbl 0085.09703 Zbl 0089.09801 Zbl 0089.09601 Zbl 0078.11003 Zbl 0042.11405 Zbl 0037.07301 Zbl 0039.33201 Zbl 0030.12601 |
Functional analysis. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functional_analysis&oldid=28195