Linear operator
linear transformation, linear map
A mapping between two vector spaces (cf. Vector space) that is compatible with their linear structures. More precisely, a mapping 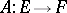 , where
, where 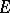 and
and 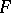 are vector spaces over a field
are vector spaces over a field 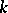 , is called a linear operator from
, is called a linear operator from 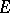 to
to 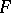 if
if
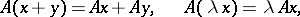 |
for all 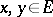 ,
, 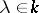 . The simplest examples are the zero linear operator
. The simplest examples are the zero linear operator 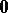 , which takes all vectors into
, which takes all vectors into 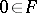 , and (in the case
, and (in the case 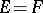 ) the identity linear operator
) the identity linear operator 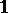 , which leaves all vectors unchanged.
, which leaves all vectors unchanged.
The concept of a linear operator, which together with the concept of a vector space is fundamental in linear algebra, plays a role in very diverse branches of mathematics and physics, above all in analysis and its applications.
The modern definition of a linear operator was first given by G. Peano [1] (for 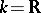 ). However, it was rooted in the previous developments of mathematics, which had accumulated (beginning with the linear function
). However, it was rooted in the previous developments of mathematics, which had accumulated (beginning with the linear function 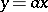 ) a vast number of examples. In algebra an incomplete list of them includes linear substitutions in systems of linear equations, and multiplication of quaternions and elements of a Grassmann algebra; in analytic geometry it includes coordinate transformations; in analysis it includes differential and integral transforms and the Fourier integral.
) a vast number of examples. In algebra an incomplete list of them includes linear substitutions in systems of linear equations, and multiplication of quaternions and elements of a Grassmann algebra; in analytic geometry it includes coordinate transformations; in analysis it includes differential and integral transforms and the Fourier integral.
Up to the beginning of the 20th century the only linear operators that had been systematically studied were those between finite-dimensional spaces over the fields 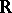 and
and 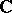 . The first "infinite-dimensional" observations, concerned also with general fields, were made by O. Toeplitz [3]. As a rule, linear operators between infinite-dimensional spaces
. The first "infinite-dimensional" observations, concerned also with general fields, were made by O. Toeplitz [3]. As a rule, linear operators between infinite-dimensional spaces 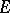 and
and 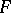 are studied under the assumption that they are continuous with respect to certain topologies. Continuous linear operators that act in various classes of topological vector spaces, in the first place Banach and Hilbert spaces, are the main object of study of linear functional analysis (cf. also Banach space; Hilbert space; Topological vector space).
are studied under the assumption that they are continuous with respect to certain topologies. Continuous linear operators that act in various classes of topological vector spaces, in the first place Banach and Hilbert spaces, are the main object of study of linear functional analysis (cf. also Banach space; Hilbert space; Topological vector space).
In the theory of linear operators the two special cases 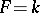 and
and  are the most important. In the first case a linear operator is called a functional (see Linear functional), and in the second case a linear transformation of $E$ (see Linear transformation), a linear operator acting in
are the most important. In the first case a linear operator is called a functional (see Linear functional), and in the second case a linear transformation of $E$ (see Linear transformation), a linear operator acting in 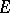 , or an endomorphism.
, or an endomorphism.
The linear operators from  to
to 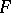 form a vector space
form a vector space 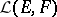 (for
(for 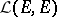 one writes
one writes 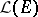 ) over
) over 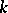 with respect to addition and multiplication by a scalar, given by the formulas
with respect to addition and multiplication by a scalar, given by the formulas
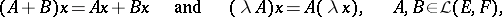 |
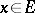 ,
, 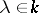 ; the zero is
; the zero is 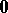 . Multiplication (composition)
. Multiplication (composition) 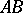 of linear operators
of linear operators 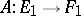 and
and 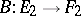 is defined only for
is defined only for 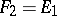 as the successive application of
as the successive application of 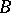 and
and 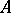 . With respect to these three operations
. With respect to these three operations 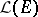 is an example of an associative algebra over
is an example of an associative algebra over 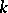 with identity
with identity 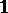 (cf. Associative rings and algebras). This is "more than an example" : Every associative algebra over
(cf. Associative rings and algebras). This is "more than an example" : Every associative algebra over 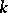 can be imbedded in an
can be imbedded in an 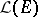 for some
for some 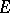 .
.
Vector spaces over a fixed field (objects) and linear operators (morphisms) form, together with the composition law, the category 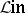 . The following concepts are special cases (in connection with
. The following concepts are special cases (in connection with  ) of general categorical concepts. For a linear operator
) of general categorical concepts. For a linear operator 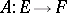 its kernel (or null-space) is the subspace
its kernel (or null-space) is the subspace  , its image is the subspace
, its image is the subspace 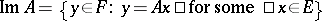 , and its cokernel is the quotient space
, and its cokernel is the quotient space  . The rank of a linear operator is the dimension of its kernel and the nullity is the dimension of its kernel. A linear operator
. The rank of a linear operator is the dimension of its kernel and the nullity is the dimension of its kernel. A linear operator 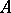 is called a monomorphism if
is called a monomorphism if  and an epimorphism if
and an epimorphism if 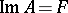 . A linear operator
. A linear operator 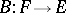 is called a left (respectively, right) inverse of
is called a left (respectively, right) inverse of 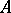 if
if 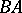 is the identity in
is the identity in 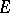 (respectively,
(respectively, 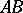 is the identity in
is the identity in 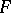 ). A linear operator
). A linear operator 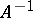 that is simultaneously the left and right inverse of
that is simultaneously the left and right inverse of 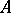 is called the inverse of
is called the inverse of 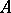 . A linear operator (respectively, endomorphism) that has an inverse is called an isomorphism (respectively, automorphism).
. A linear operator (respectively, endomorphism) that has an inverse is called an isomorphism (respectively, automorphism).
The category 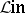 is an Abelian category with respect to addition of linear operators; in particular, a linear operator that is a monomorphism and an epimorphism is an isomorphism. Moreover, in
is an Abelian category with respect to addition of linear operators; in particular, a linear operator that is a monomorphism and an epimorphism is an isomorphism. Moreover, in  every monomorphism has a left inverse and every epimorphism has a right inverse. By analogy with
every monomorphism has a left inverse and every epimorphism has a right inverse. By analogy with 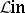 one introduces the categories
one introduces the categories 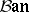 and
and 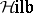 ; the objects of the first are Banach spaces, and the objects of the second are Hilbert spaces; the morphisms in both are continuous linear operators. Both categories are additive (cf. Additive category), but not Abelian. Isomorphisms in them are called topological isomorphisms; these are linear operators that have a continuous inverse.
; the objects of the first are Banach spaces, and the objects of the second are Hilbert spaces; the morphisms in both are continuous linear operators. Both categories are additive (cf. Additive category), but not Abelian. Isomorphisms in them are called topological isomorphisms; these are linear operators that have a continuous inverse.
One of the most important typical problems of the "intrinsic" theory of linear operators is the problem of classifying endomorphisms (or at least certain classes of them) with respect to some equivalence or other. For linear operators in pure algebra one considers, as a rule, the general categorical equivalence of endomorphisms in 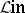 ; it is called similarity. In other words, linear operators
; it is called similarity. In other words, linear operators 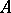 and
and 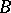 acting in
acting in 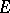 and
and 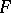 , respectively, are similar if for some isomorphism
, respectively, are similar if for some isomorphism 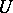 the diagram
the diagram
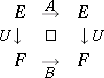 | (1) |
commutes. Equivalence of continuous linear operators in (general) Banach spaces is called topological equivalence, and is understood in the general categorical sense, this time in 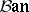 ; this implies that the diagram (1) commutes for some topological isomorphism
; this implies that the diagram (1) commutes for some topological isomorphism 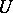 . For linear operators in Hilbert spaces one chooses unitary equivalence of
. For linear operators in Hilbert spaces one chooses unitary equivalence of 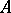 and
and 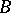 as basis, corresponding to the requirement that the diagram (1) commutes for some unitary (see below) operator
as basis, corresponding to the requirement that the diagram (1) commutes for some unitary (see below) operator 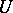 .
.
Besides this, in the theory of linear operators between spaces with a topology there are important problems of approximating various classes of linear operators by operators of a comparatively simple structure. A significant role is played by problems about finding the general form of linear operators on concrete spaces, most frequently function spaces.
Among the invariants of similarity the most important are the spectrum and the number of invariant subspaces of given dimension. Let 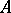 be a linear operator on
be a linear operator on  . Its spectrum is the subset
. Its spectrum is the subset 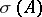 in
in 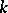 consisting of those
consisting of those 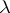 for which
for which 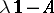 has no inverse. A subspace
has no inverse. A subspace 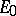 of
of 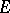 is said to be invariant with respect to
is said to be invariant with respect to 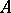 if
if 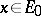 implies that
implies that 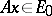 . Besides the kernel and the image of a linear operator, examples are the one-dimensional subspaces containing the so-called eigen vectors of the operator, that is, those
. Besides the kernel and the image of a linear operator, examples are the one-dimensional subspaces containing the so-called eigen vectors of the operator, that is, those 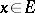 ,
, 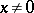 , for which
, for which 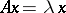 ,
, 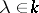 . The element
. The element 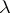 , called an eigen value of
, called an eigen value of 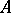 , automatically belongs to
, automatically belongs to 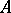 's spectrum.
's spectrum.
The concept of a linear operator is a special case of the concept of a morphism of modules, which is obtained by replacing the field by an arbitrary ring. In many respects morphisms of modules are not like linear operators in their properties, but results about the latter form one of the stimuli for studying them.
Linear operators on finite-dimensional spaces
(without additional structure). The main analytic apparatus for such linear operators is the matrix notation. Let 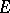 and
and 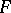 be spaces with fixed bases
be spaces with fixed bases 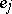 ,
, 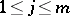 , and
, and 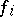 ,
, 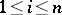 , let
, let 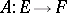 be a linear operator, and let
be a linear operator, and let 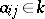 be the
be the 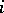 -th coefficients of the expansion of
-th coefficients of the expansion of 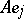 with respect to the second basis. Then the
with respect to the second basis. Then the 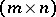 -dimensional matrix
-dimensional matrix 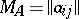 is called the matrix of the linear operator
is called the matrix of the linear operator 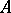 in the bases
in the bases 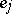 and
and 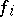 . If
. If 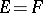 the matrix notation is usually taken in coincident bases (that is,
the matrix notation is usually taken in coincident bases (that is, 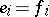 ,
, 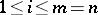 ). By transfer to other bases the matrix of a linear operator is changed by simple formulas.
). By transfer to other bases the matrix of a linear operator is changed by simple formulas.
To various characteristics of linear operators correspond, as a rule, effectively computable characteristics of their matrices. For example, 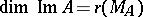 and
and 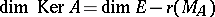 , where
, where  is the rank of the matrix; in particular,
is the rank of the matrix; in particular, 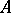 is an isomorphism if and only if
is an isomorphism if and only if 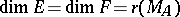 ; this condition is equivalent to the determinant of
; this condition is equivalent to the determinant of 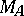 being non-zero. To algebraic operations on linear operators correspond operations of the same name on their matrices, taken in fixed bases.
being non-zero. To algebraic operations on linear operators correspond operations of the same name on their matrices, taken in fixed bases.
Linear operators are similar if and only if they can be described (each in its "own" basis) by the same matrix. The eigen values of a linear operator are the roots of the characteristic polynomial of its matrix. This implies that every linear operator on a finite-dimensional space over an algebraically closed field (for example, 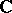 ) has at least one eigen vector. The spectrum of a linear operator on a finite-dimensional space over an arbitrary field is the set of its eigen values.
) has at least one eigen vector. The spectrum of a linear operator on a finite-dimensional space over an arbitrary field is the set of its eigen values.
The problem of classifying endomorphisms of finite-dimensional spaces over an algebraically closed field has been completely solved, and the similarity classes have been described in terms of the invariant subspaces. The main step here is the following classification theorem, discovered by C. Jordan (who considered the field 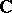 ). A matrix with a fixed
). A matrix with a fixed 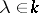 on the main diagonal, ones immediately above it and zeros elsewhere, is called a Jordan block, and a block matrix with Jordan blocks (of different dimensions and with different
on the main diagonal, ones immediately above it and zeros elsewhere, is called a Jordan block, and a block matrix with Jordan blocks (of different dimensions and with different 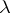 ) on the main diagonal and zeros elsewhere is called a Jordan matrix. Then every endomorphism can be written in some basis as a Jordan matrix. The search for such a basis is called reduction of a linear operator to Jordan form. Since linear operators described by Jordan matrices are similar if and only if their matrices coincide up to a permutation of the Jordan blocks, the theorem means that Jordan matrices present, after suitable identification, a complete set of similarity invariants.
) on the main diagonal and zeros elsewhere is called a Jordan matrix. Then every endomorphism can be written in some basis as a Jordan matrix. The search for such a basis is called reduction of a linear operator to Jordan form. Since linear operators described by Jordan matrices are similar if and only if their matrices coincide up to a permutation of the Jordan blocks, the theorem means that Jordan matrices present, after suitable identification, a complete set of similarity invariants.
Continuous linear operators on Banach spaces.
The foundations of this theory were laid by S. Banach (see [4]).
Examples.
1) In 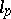 (from now on,
(from now on, 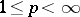 ): the linear operator of multiplication by a bounded sequence of numbers; the linear operator of left (respectively, right) shift, which takes
): the linear operator of multiplication by a bounded sequence of numbers; the linear operator of left (respectively, right) shift, which takes 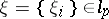 to
to  (respectively, to
(respectively, to 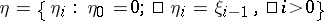 ).
).
2) In 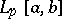 or
or 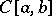 : the linear operator of multiplication by a continuous function
: the linear operator of multiplication by a continuous function 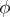 on
on 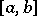 ; the linear operator of indefinite integration, which takes
; the linear operator of indefinite integration, which takes 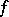 to
to 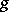 ,
,
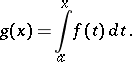 |
3) In 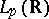 : the linear operator of a shift by
: the linear operator of a shift by 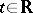 , which takes
, which takes 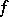 to
to 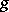 ,
, 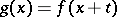 .
.
4) From 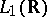 into
into 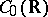 : The "classical" Fourier operator, which takes
: The "classical" Fourier operator, which takes 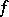 to
to 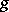 ,
,
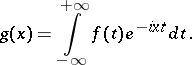 |
A linear operator 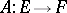 between Banach spaces is continuous if and only if it is bounded, that is, the image of every bounded set in
between Banach spaces is continuous if and only if it is bounded, that is, the image of every bounded set in 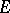 is bounded in
is bounded in 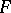 , or equivalently, if there is a (finite) number
, or equivalently, if there is a (finite) number 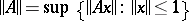 , called the operator norm (a similar assertion is also true for arbitrary normed spaces). The continuous linear operators from
, called the operator norm (a similar assertion is also true for arbitrary normed spaces). The continuous linear operators from 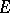 into
into 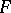 form a subspace
form a subspace 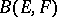 of
of 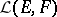 which is a Banach space with respect to
which is a Banach space with respect to 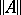 . The subspace
. The subspace 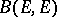 , often denoted by
, often denoted by 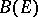 , is even a Banach algebra with respect to operator multiplication. The class of these algebras is universal in the sense that every Banach algebra is topologically isomorphic to a subalgebra of
, is even a Banach algebra with respect to operator multiplication. The class of these algebras is universal in the sense that every Banach algebra is topologically isomorphic to a subalgebra of 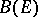 for some
for some 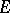 . The subset of
. The subset of 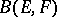 consisting of topological isomorphisms is open and for
consisting of topological isomorphisms is open and for 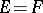 contains the open ball of unit radius with centre at
contains the open ball of unit radius with centre at 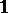 .
.
A fundamental role in the "Banach" theory of linear operators is played by two theorems, which together with the Hahn–Banach theorem (see also Linear functional) are called the three fundamental principles of linear analysis. The simplest form of the "principle of uniform boundedness" is the Banach–Steinhaus theorem: If continuous linear operators  ,
, 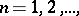 are such that for every
are such that for every 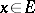 one has
one has 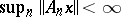 , then
, then  . The simplest form of the "open mapping principle" is Banach's theorem: If a continuous linear operator has an inverse, then this inverse operator is automatically continuous. The requirement that the spaces be "Banach" (complete) spaces is essential in both theorems.
. The simplest form of the "open mapping principle" is Banach's theorem: If a continuous linear operator has an inverse, then this inverse operator is automatically continuous. The requirement that the spaces be "Banach" (complete) spaces is essential in both theorems.
The spectrum of a continuous linear operator 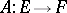 , usually considered for complex spaces, is a non-empty compact set in
, usually considered for complex spaces, is a non-empty compact set in 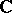 . In the case of an infinite-dimensional space the set of eigen values of a linear operator, called the point spectrum, generally forms only part of
. In the case of an infinite-dimensional space the set of eigen values of a linear operator, called the point spectrum, generally forms only part of 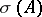 . For the remaining
. For the remaining 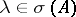 one always has
one always has 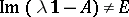 ; these numbers split into two sets, the continuous spectrum and the residual spectrum, according as
; these numbers split into two sets, the continuous spectrum and the residual spectrum, according as 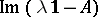 is dense in
is dense in 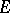 or not. For example, the spectrum of the linear operator of multiplication by
or not. For example, the spectrum of the linear operator of multiplication by 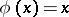 is the interval
is the interval 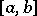 , but in the case of spaces
, but in the case of spaces 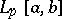 all its points belong to the continuous spectrum, and in the case
all its points belong to the continuous spectrum, and in the case 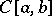 they belong to the residual spectrum.
they belong to the residual spectrum.
The operator-valued function 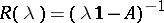 defined on
defined on 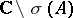 is called the resolvent of the linear operator
is called the resolvent of the linear operator 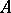 . It is useful, particularly because for every function
. It is useful, particularly because for every function 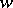 , holomorphic in some neighbourhood
, holomorphic in some neighbourhood 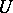 of the spectrum, it makes it possible to consider the linear operator (denoted by
of the spectrum, it makes it possible to consider the linear operator (denoted by 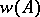 )
)
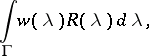 |
where 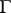 is a smooth contour in
is a smooth contour in 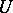 that bounds the spectrum. In this way one can construct a "holomorphic operator calculus" ; as for "holomorphic multi-operator calculus" , that is, loosely speaking, giving a reasonable sense to the concept of a holomorphic function of several "operator" variables, the problem of constructing it turned out to be far more difficult. Results that are in a certain sense close to final have been obtained by methods of homological algebra [5].
that bounds the spectrum. In this way one can construct a "holomorphic operator calculus" ; as for "holomorphic multi-operator calculus" , that is, loosely speaking, giving a reasonable sense to the concept of a holomorphic function of several "operator" variables, the problem of constructing it turned out to be far more difficult. Results that are in a certain sense close to final have been obtained by methods of homological algebra [5].
In the theory of linear operators between Banach spaces an important operation is that of going over from  to its so-called adjoint linear operator
to its so-called adjoint linear operator 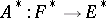 (cf. also Adjoint operator), which is defined by the formula
(cf. also Adjoint operator), which is defined by the formula
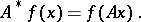 |
This operation has the properties
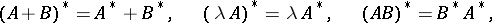 |
 |
(on the assumption that the left-hand sides of the equalities make sense). If  and
and 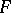 are reflexive (cf. Reflexive space), then
are reflexive (cf. Reflexive space), then 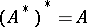 .
.
Some of the most important classes of linear operators in Banach spaces are the following.
1) 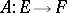 is called a compact operator, or a completely-continuous operator, if it maps any bounded set in
is called a compact operator, or a completely-continuous operator, if it maps any bounded set in 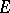 to a totally-bounded (that is, pre-compact) set in
to a totally-bounded (that is, pre-compact) set in 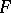 . Every linear operator that can be approximated in the operator norm by finite-dimensional (having finite-dimensional image) linear operators is compact. For the overwhelming majority of classical Banach spaces
. Every linear operator that can be approximated in the operator norm by finite-dimensional (having finite-dimensional image) linear operators is compact. For the overwhelming majority of classical Banach spaces 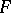 the converse is also true: Every compact linear operator from any
the converse is also true: Every compact linear operator from any 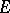 to
to 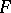 can be approximated by finite-dimensional operators. The so-called approximation problem (is this true for all
can be approximated by finite-dimensional operators. The so-called approximation problem (is this true for all 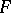 ?) has been negatively answered [6].
?) has been negatively answered [6].
The identity linear operator in 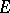 is compact if and only if
is compact if and only if 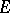 is finite dimensional (Riesz' theorem). The spectrum of a compact linear operator is a set containing
is finite dimensional (Riesz' theorem). The spectrum of a compact linear operator is a set containing  that is at most countable. If the spectrum is infinite, then
that is at most countable. If the spectrum is infinite, then  is the unique limit point of it. Every
is the unique limit point of it. Every 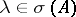 ,
, 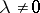 , is an eigen value, and the eigen vectors corresponding to it form a finite-dimensional space.
, is an eigen value, and the eigen vectors corresponding to it form a finite-dimensional space.
2) 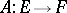 is called a nuclear operator if it can be represented as an absolutely convergent series in
is called a nuclear operator if it can be represented as an absolutely convergent series in 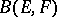 consisting of one-dimensional linear operators; such an operator is necessarily compact. By means of nuclear linear operators one can define a class of topological vector spaces, called nuclear spaces, which is important in analysis (cf. Nuclear space).
consisting of one-dimensional linear operators; such an operator is necessarily compact. By means of nuclear linear operators one can define a class of topological vector spaces, called nuclear spaces, which is important in analysis (cf. Nuclear space).
3) 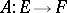 is called a Fredholm operator if its kernel and cokernel are finite dimensional; the image of such a linear operator is necessarily closed. The main characteristic of a linear Fredholm operator is its index
is called a Fredholm operator if its kernel and cokernel are finite dimensional; the image of such a linear operator is necessarily closed. The main characteristic of a linear Fredholm operator is its index  . The set of linear Fredholm operators is open in
. The set of linear Fredholm operators is open in 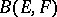 and the index on it (in contrast to the dimensions of the kernel and cokernel taken separately) is a locally constant function. The forerunner of the theory of linear Fredholm operators was the theory of integral equations. Set up by E. Fredholm, who essentially proved (and D. Hilbert perceived this "geometrical" background) that a linear operator of the form
and the index on it (in contrast to the dimensions of the kernel and cokernel taken separately) is a locally constant function. The forerunner of the theory of linear Fredholm operators was the theory of integral equations. Set up by E. Fredholm, who essentially proved (and D. Hilbert perceived this "geometrical" background) that a linear operator of the form 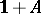 with compact
with compact 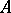 is a Fredholm operator and has index zero (see Fredholm alternative). Important specific classes of linear Fredholm operators arise in considering elliptic differential expressions on manifolds. The problem of calculating their index required the apparatus of algebraic topology [8] (cf. also Index formulas).
is a Fredholm operator and has index zero (see Fredholm alternative). Important specific classes of linear Fredholm operators arise in considering elliptic differential expressions on manifolds. The problem of calculating their index required the apparatus of algebraic topology [8] (cf. also Index formulas).
The problem of classifying endomorphisms of Banach spaces, in view of Jordan's theorem, which gives a finite-dimensional model of its solution, can be treated "to a first approximation" as the problem of constructing an appropriate infinite-dimensional analogue of the Jordan form of a linear operator. However, it is far from being solved: to say nothing about a "sufficient" set of invariant subspaces, it is not known so far (1989) whether every operator that acts on a Hilbert space 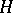 has at least one non-trivial (distinct from
has at least one non-trivial (distinct from 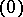 and
and 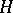 ) invariant subspace. If a linear operator
) invariant subspace. If a linear operator 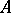 that acts on an arbitrary Banach space is not proportional to
that acts on an arbitrary Banach space is not proportional to 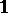 and commutes with some compact linear operator, then the set of all linear operators that commute with
and commutes with some compact linear operator, then the set of all linear operators that commute with 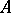 is a non-trivial invariant subspace (see [9]).
is a non-trivial invariant subspace (see [9]).
Apart from the topology of a normed space, there are topologies in 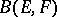 that specify the structure of a locally convex space in it. The most important are the strong and weak operator topologies, specified, respectively, by the systems of semi-norms
that specify the structure of a locally convex space in it. The most important are the strong and weak operator topologies, specified, respectively, by the systems of semi-norms
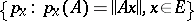 |
and
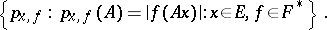 |
The theory of continuous linear operators on topological vector spaces (an example of such a linear operator is the Fourier transform on generalized functions) was developed on the basis of the "Banach" theory. A significant place in it is taken by the investigation of the possibility of generalizing Banach's classical theorems and others; it led to the introduction of a number of important classes of spaces. For example, the theorem on the equivalence of continuity and boundedness, the Banach–Steinhaus theorem and Banach's theorem on the inverse operator are not true for arbitrary, at least locally convex, separable complete spaces. At the same time, the first of these theorems is true if 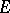 is a bornological space, the second if
is a bornological space, the second if 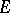 is a barrelled space, and the third if
is a barrelled space, and the third if 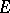 is absolutely complete and
is absolutely complete and  is a barrelled space.
is a barrelled space.
Continuous linear operators on Hilbert spaces
(finite-dimensional and infinite-dimensional). Their theory was first formalized in the work of Hilbert [10] on integral equations and infinite quadratic forms.
Examples.
1) All examples of linear operators in 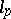 ,
, 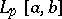 ,
, 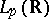 considered above, for
considered above, for 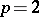 .
.
2) The integral operator in 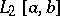 that takes
that takes 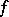 to
to 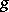 ,
,
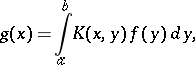 |
where 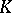 is a square-integrable function on the set
is a square-integrable function on the set 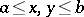 . Such a linear operator is always compact.
. Such a linear operator is always compact.
3) The Fourier operator in 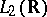 is uniquely defined by the fact that it coincides with the classical Fourier operator (see above) on
is uniquely defined by the fact that it coincides with the classical Fourier operator (see above) on 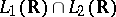 .
.
The concepts and facts are given below in the form that they have for spaces over 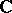 : namely, in complex spaces the theory has turned out to be most important and meaningful.
: namely, in complex spaces the theory has turned out to be most important and meaningful.
The special position of the "Hilbert" theory of linear operators in the background of the "Banach" theory is determined by the sharply increasing role of the concept of the adjoint operator. Since a Hilbert space 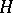 and its adjoint
and its adjoint 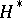 are anti-isomorphic, the linear operator
are anti-isomorphic, the linear operator 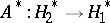 is naturally identified with the linear operator from
is naturally identified with the linear operator from 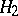 to
to 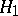 uniquely defined by
uniquely defined by 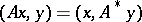 ,
, 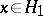 ,
, 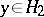 ; under this identification the linear operator adjoint to an endomorphism in
; under this identification the linear operator adjoint to an endomorphism in 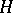 again acts in
again acts in 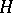 . In
. In 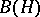 there arises an important additional structure — the operation of transition from
there arises an important additional structure — the operation of transition from 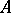 to
to 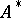 , which has involutory properties and with respect to which
, which has involutory properties and with respect to which 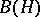 is a
is a 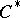 -algebra. In fact, every
-algebra. In fact, every 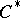 -algebra is isometrically
-algebra is isometrically  -isomorphic to a
-isomorphic to a 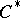 -subalgebra of
-subalgebra of 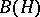 for some
for some 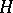 (the Gel'fand–Naimark theorem).
(the Gel'fand–Naimark theorem).
The following classes of linear operators are characteristic of Hilbert spaces.
A linear operator 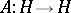 is called a self-adjoint operator, or a Hermitian operator, if
is called a self-adjoint operator, or a Hermitian operator, if  . A self-adjoint linear operator equal to its square is called a projector (projection operator); such a linear operator can be realized as the operator of orthogonal projection onto a closed subspace of
. A self-adjoint linear operator equal to its square is called a projector (projection operator); such a linear operator can be realized as the operator of orthogonal projection onto a closed subspace of 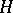 . A linear operator
. A linear operator 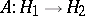 is called a unitary operator (in the case of the field
is called a unitary operator (in the case of the field 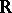 , an orthogonal operator) if
, an orthogonal operator) if 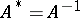 , or, equivalently, if
, or, equivalently, if  ,
, 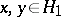 and
and 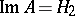 . A linear operator is unitary if and only if it is an isomorphism that preserves norms. Self-adjoint and unitary endomorphisms are special cases of a normal operator: A linear operator
. A linear operator is unitary if and only if it is an isomorphism that preserves norms. Self-adjoint and unitary endomorphisms are special cases of a normal operator: A linear operator 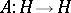 such that
such that 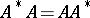 .
.
The linear operator of multiplication by a sequence (respectively, a function) in 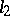 (respectively, in
(respectively, in 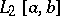 ) is self-adjoint if and only if this sequence (function) is real valued. A linear integral operator is self-adjoint if and only if
) is self-adjoint if and only if this sequence (function) is real valued. A linear integral operator is self-adjoint if and only if  almost-everywhere. In
almost-everywhere. In 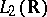 shift operators and the Fourier operator are unitary. In
shift operators and the Fourier operator are unitary. In 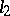 the linear operators of left and right shift are adjoint to one another and are not normal. The spectrum of a self-adjoint linear operator lies in
the linear operators of left and right shift are adjoint to one another and are not normal. The spectrum of a self-adjoint linear operator lies in  , and the spectrum of a unitary operator lies on the unit circle in
, and the spectrum of a unitary operator lies on the unit circle in 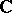 . The spectrum of a projector
. The spectrum of a projector 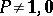 consists of the points
consists of the points  and
and 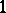 . The spectrum of a normal linear operator can be any compact set in
. The spectrum of a normal linear operator can be any compact set in 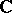 . The eigen vectors of a self-adjoint linear operator corresponding to different eigen values are orthogonal.
. The eigen vectors of a self-adjoint linear operator corresponding to different eigen values are orthogonal.
The classes of linear operators described above are used in a large number of branches of mathematics and physics, including quantum mechanics (where self-adjoint linear operators are interpreted as observables), the theory of representations and harmonic analysis, the theory of differential equations, and the theory of dynamical systems.
All information about a linear operator acting in a finite-dimensional Hilbert space is provided by its matrix notation in an orthogonal basis. In this notation transition to the adjoint linear operator corresponds to taking the matrix that is the complex conjugate of the transposed matrix; as a consequence, for the matrix 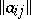 of a self-adjoint linear operator one has
of a self-adjoint linear operator one has 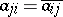 . The classical theorem "on reduction to diagonal form" asserts that every normal (in the case of the field
. The classical theorem "on reduction to diagonal form" asserts that every normal (in the case of the field  , every self-adjoint) linear operator can be written in some orthonormal basis as a diagonal matrix. Together with the fact that linear operators are unitarily equivalent if and only if they can be described (each in its own orthogonal basis) by the same matrices, this theorem implies that the sets of eigen values (taking account of their multiplicity) form a complete system of invariants of unitary equivalence for normal linear operators.
, every self-adjoint) linear operator can be written in some orthonormal basis as a diagonal matrix. Together with the fact that linear operators are unitarily equivalent if and only if they can be described (each in its own orthogonal basis) by the same matrices, this theorem implies that the sets of eigen values (taking account of their multiplicity) form a complete system of invariants of unitary equivalence for normal linear operators.
The theorem on reduction to diagonal form turned out to be "happier" than Jordan's theorem in that a meaningful infinite-dimensional analogue was found for it, the spectral theorem for normal linear operators, discovered in 1912: A normal linear operator can be represented uniquely as an operator-valued Stieltjes integral 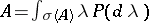 , where
, where 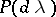 is a countably-additive regular (in the sense of the strong operator topology, for example) function on the Borel subsets of
is a countably-additive regular (in the sense of the strong operator topology, for example) function on the Borel subsets of 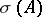 that takes values among projectors and is such that
that takes values among projectors and is such that 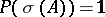 (see Spectral measure). A consequence is that every normal linear operator can be approximated by linear combinations of projectors.
(see Spectral measure). A consequence is that every normal linear operator can be approximated by linear combinations of projectors.
On the basis of Hilbert's theorem a complete classification up to unitary equivalence of normal linear operators (in a space of arbitrary dimension) has been obtained [11]; in particular, it turns out that every normal linear operator is unitarily equivalent to the operator of multiplication by a bounded measurable function in 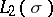 , where
, where 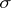 is a measurable space with finite measure. For compact normal linear operators in a separable space the picture is simplified: such a linear operator has as orthonormal basis its own eigen vectors and is therefore unitarily equivalent to the operator of multiplication by a sequence acting in
is a measurable space with finite measure. For compact normal linear operators in a separable space the picture is simplified: such a linear operator has as orthonormal basis its own eigen vectors and is therefore unitarily equivalent to the operator of multiplication by a sequence acting in 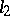 (the sequence necessarily converges to zero).
(the sequence necessarily converges to zero).
In the case of a normal 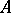 the spectral theorem makes it possible to assign a meaning to the function expression
the spectral theorem makes it possible to assign a meaning to the function expression 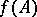 for a wider class of functions on the spectrum than holomorphic functions, for example, for a continuous
for a wider class of functions on the spectrum than holomorphic functions, for example, for a continuous 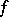 the linear operator
the linear operator 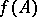 is defined as
is defined as 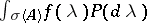 . If
. If 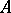 is self-adjoint, then the linear operator
is self-adjoint, then the linear operator 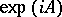 is unitary.
is unitary.
The main effort has been concentrated on the study of different classes of non-normal linear operators, in the first place abstract Volterra operators, condensing operators and spectral operators (see [11]–[13], and Volterra operator; Spectral operator; Condensing operator). Although regularities comparable with the regularity in the spectral theorem have still (1989) not been discovered, nevertheless deep results have been obtained in this direction.
The development of analysis and its applications, in the first place differential equations and quantum mechanics, forces one to go beyond the class of bounded (that is, continuous) linear operators. Strictly speaking, an unbounded operator 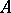 in
in 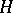 is not a linear operator in the sense accepted here, since it is defined not on the whole of
is not a linear operator in the sense accepted here, since it is defined not on the whole of 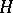 , but only on a dense subspace of it, as a rule. Typical examples are the linear operator of multiplication by
, but only on a dense subspace of it, as a rule. Typical examples are the linear operator of multiplication by  and differentiation in
and differentiation in 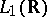 . For unbounded linear operators analogues of the spectrum, the adjoint linear operator and the classes of linear operators considered above have been defined. Although their theory is more complicated than the theory of bounded linear operators, a number of deep results of the latter has been generalized meaningfully. The most important of these is an analogue of the spectral theorem, discovered by J. von Neumann for unbounded self-adjoint operators.
. For unbounded linear operators analogues of the spectrum, the adjoint linear operator and the classes of linear operators considered above have been defined. Although their theory is more complicated than the theory of bounded linear operators, a number of deep results of the latter has been generalized meaningfully. The most important of these is an analogue of the spectral theorem, discovered by J. von Neumann for unbounded self-adjoint operators.
References
| [1] | G. Peano, "Calcolo geometrico secondo l'Ausdehnungslehre di H. Grassmann" , Bocca (1888) |
| [2] | I.M. Gel'fand, "Lectures on linear algebra" , Interscience (1961) (Translated from Russian) Zbl 0098.01108 |
| [3] | O. Toeplitz, "Ueber die Auflösung unendlichvieler linearer Gleichungen mit unendlichvielen Unbekannten" Rend. Circolo Mat. Palermo , 28 (1909) pp. 88–96 |
| [4] | S.S. Banach, "A course of functional analysis" , Kiev (1948) (In Ukrainian) |
| [5] | J.L. Taylor, "A general framework for a multi-operator functional calculus" Advances in Math. , 9 : 2 (1972) pp. 183–252 MR0328625 |
| [6] | P. Enflo, "A counterexample to the approximation problem in Banach spaces" Acta Math. , 130 (1973) pp. 309–317 MR0402468 Zbl 0267.46012 |
| [7] | H.H. Schaefer, "Topological vector spaces" , Macmillan (1966) MR0193469 Zbl 0141.30503 |
| [8] | , Functional analysis , Math. Reference Library , Moscow (1972) (In Russian) |
| [9] | V.I. Lomonosov, "Invariant subspaces of a family of operators that commute with a completely continuous operator" Funktsional. Anal. i Prilozhen. , 3 (1973) pp. 55–56 (In Russian) MR420305 |
| [10] | D. Hilbert, "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen" , Chelsea, reprint (1953) MR0056184 Zbl 0050.10201 |
| [11] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) MR0117523 |
| [12] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral theory" , 2 , Interscience (1963) MR0188745 |
| [13] | N. Dunford, J.T. Schwartz, "Linear operators. Spectral operators" , 3 , Interscience (1971) MR0412888 |
| [14] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Theory and applications of Volterra operators in Hilbert space" , Amer. Math. Soc. (1970) (Translated from Russian) MR0264447 Zbl 0194.43804 |
| [15] | B. Szökefalvi-Nagy, Ch. Foiaş, "Harmonic analysis of operators on Hilbert space" , North-Holland (1970) (Translated from French) MR275190 |
| [16] | N. Bourbaki, "Elements of mathematics. Algebra: Modules. Rings. Forms" , 2 , Addison-Wesley (1975) pp. Chapt.4;5;6 (Translated from French) MR2333539 MR2327161 MR2325344 MR2284892 MR2272929 MR0928386 MR0896478 MR0782297 MR0782296 MR0722608 MR0682756 MR0643362 MR0647314 MR0610795 MR0583191 MR0354207 MR0360549 MR0237342 MR0205211 MR0205210 |
Comments
For a fairly recent text on multi-dimensional functional calculus cf. [a6].
References
| [a1] | I.C. Gohberg, S. Goldberg, "Basic operator theory" , Birkhäuser (1977) MR1843182 MR0632943 Zbl 0990.47001 Zbl 0458.47001 |
| [a2] | I.C. [I.Ts. Gokhberg] Gohberg, M.G. Krein, "Introduction to the theory of linear nonselfadjoint operators" , Transl. Math. Monogr. , 18 , Amer. Math. Soc. (1969) (Translated from Russian) MR0246142 Zbl 0181.13504 |
| [a3] | P.R. Halmos, "Finite-dimensional vector spaces" , v. Nostrand (1958) MR0089819 Zbl 0107.01404 |
| [a4] | A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983) MR0710486 Zbl 0516.47023 |
| [a5] | C. Pearcy (ed.) , Topics in operator theory , Amer. Math. Soc. (1974) MR0350446 Zbl 0291.00011 |
| [a6] | F.H. Vasilescu, "Analytic functional calculus and spectral decompositions" , Reidel (1982) MR0690957 Zbl 0495.47013 |
Linear operator. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_operator&oldid=42219