Abelian variety
An algebraic group that is a complete algebraic variety. The completeness condition implies severe restrictions on an Abelian variety. Thus, an Abelian variety can be imbedded as a closed subvariety in a projective space; each rational mapping of a non-singular variety into an Abelian variety is regular; the group law on an Abelian variety is commutative.
The theory of Abelian varieties over the field of complex numbers  is, in essence, equivalent to the theory of Abelian functions founded by C.G.J. Jacobi, N.H. Abel and B. Riemann. If
is, in essence, equivalent to the theory of Abelian functions founded by C.G.J. Jacobi, N.H. Abel and B. Riemann. If  denotes
denotes  -dimension vector space,
-dimension vector space,  is a lattice (cf. Discrete subgroup) of rank
is a lattice (cf. Discrete subgroup) of rank  , then the quotient group
, then the quotient group  is a complex torus. Meromorphic functions on
is a complex torus. Meromorphic functions on  are the same thing as meromorphic functions on
are the same thing as meromorphic functions on  that are invariant with respect to the period lattice
that are invariant with respect to the period lattice  . If the field
. If the field 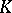 of meromorphic functions on
of meromorphic functions on  has transcendence degree
has transcendence degree  , then
, then 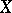 can be given the structure of an algebraic group. This structure is unique by virtue of the compactness of
can be given the structure of an algebraic group. This structure is unique by virtue of the compactness of 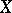 , and it is such that the field of rational functions of this structure coincides with
, and it is such that the field of rational functions of this structure coincides with 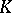 . The algebraic groups formed in this way are Abelian varieties, and each Abelian variety over the field
. The algebraic groups formed in this way are Abelian varieties, and each Abelian variety over the field 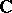 arises in this way. The matrix which defines a basis of
arises in this way. The matrix which defines a basis of  can be reduced to the form
can be reduced to the form 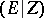 , where
, where 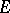 is the identity matrix and
is the identity matrix and 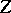 is a matrix of order
is a matrix of order 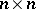 . The complex torus
. The complex torus  is an Abelian variety if and only if
is an Abelian variety if and only if 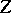 is symmetric and has positive-definite imaginary part. It should be pointed out that, as real Lie groups, all varieties
is symmetric and has positive-definite imaginary part. It should be pointed out that, as real Lie groups, all varieties 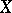 are isomorphic, but this is not true for their analytic or algebraic structures, which vary strongly when deforming the lattice
are isomorphic, but this is not true for their analytic or algebraic structures, which vary strongly when deforming the lattice 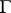 . Inspection of the period matrix
. Inspection of the period matrix 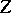 shows that its variation has an analytic character, which results in the construction of the moduli variety of all Abelian varieties of given dimension
shows that its variation has an analytic character, which results in the construction of the moduli variety of all Abelian varieties of given dimension  . The dimension of the moduli variety is
. The dimension of the moduli variety is 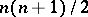 (cf. Moduli problem).
(cf. Moduli problem).
The theory of Abelian varieties over an arbitrary field  is due to A. Weil [1], [2]. It has numerous applications both in algebraic geometry itself and in other fields of mathematics, particularly in number theory and in the theory of automorphic functions. To each complete algebraic variety, Abelian varieties (cf. Albanese variety; Picard variety; Intermediate Jacobian) can be functorially assigned. These constructions are powerful tools in studying the geometric structures of algebraic varieties. E.g., they were used to obtain one of the solutions of the Lüroth problem. Another application is the proof of the Riemann hypothesis for algebraic curves over a finite field — the problem for which the abstract theory of Abelian varieties was originally developed. It was also one of the sources of
is due to A. Weil [1], [2]. It has numerous applications both in algebraic geometry itself and in other fields of mathematics, particularly in number theory and in the theory of automorphic functions. To each complete algebraic variety, Abelian varieties (cf. Albanese variety; Picard variety; Intermediate Jacobian) can be functorially assigned. These constructions are powerful tools in studying the geometric structures of algebraic varieties. E.g., they were used to obtain one of the solutions of the Lüroth problem. Another application is the proof of the Riemann hypothesis for algebraic curves over a finite field — the problem for which the abstract theory of Abelian varieties was originally developed. It was also one of the sources of 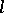 -adic cohomology. The simplest example of such a cohomology is the Tate module of an Abelian variety. It is the projective limit, as
-adic cohomology. The simplest example of such a cohomology is the Tate module of an Abelian variety. It is the projective limit, as 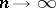 , of the groups
, of the groups  of points of order
of points of order  . The determination of the structure of such groups was one of the principal achievements of the theory of Weil. In fact, if
. The determination of the structure of such groups was one of the principal achievements of the theory of Weil. In fact, if  is coprime with the characteristic
is coprime with the characteristic  of the field
of the field 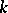 and if
and if 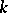 is algebraically closed, then the group
is algebraically closed, then the group 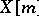 is isomorphic to
is isomorphic to 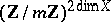 . If
. If 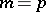 , the situation is more complicated, which resulted in the appearance of concepts such as finite group schemes, formal groups and
, the situation is more complicated, which resulted in the appearance of concepts such as finite group schemes, formal groups and  -divisible groups (cf. Finite group scheme; Formal group;
-divisible groups (cf. Finite group scheme; Formal group;  -divisible group). The study of the action of endomorphisms of Abelian varieties, in particular of the Frobenius endomorphism on its Tate module, makes it possible to give a proof of the Riemann hypothesis (for algebraic curves over finite fields, cf. Riemann hypotheses) and is also the principal instrument in the theory of complex multiplication of Abelian varieties. Another circle of problems connected with the Tate module consists of a study of the action of the Galois group of the closure of the ground field on this module. There resulted the Tate conjectures and the theory of Tate–Honda, which describes Abelian varieties over finite fields in terms of the Tate module [5].
-divisible group). The study of the action of endomorphisms of Abelian varieties, in particular of the Frobenius endomorphism on its Tate module, makes it possible to give a proof of the Riemann hypothesis (for algebraic curves over finite fields, cf. Riemann hypotheses) and is also the principal instrument in the theory of complex multiplication of Abelian varieties. Another circle of problems connected with the Tate module consists of a study of the action of the Galois group of the closure of the ground field on this module. There resulted the Tate conjectures and the theory of Tate–Honda, which describes Abelian varieties over finite fields in terms of the Tate module [5].
The study of Abelian varieties over local fields, including 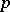 -adic fields, is proceeding at a fast rate. An analogue of the above-mentioned representation of Abelian varieties as a quotient space
-adic fields, is proceeding at a fast rate. An analogue of the above-mentioned representation of Abelian varieties as a quotient space  , usually known as uniformization, over such fields, was constructed by D. Mumford and M. Raynaud. Unlike the complex case, not all Abelian varieties, but only those having a reduction to a multiplicative group modulo
, usually known as uniformization, over such fields, was constructed by D. Mumford and M. Raynaud. Unlike the complex case, not all Abelian varieties, but only those having a reduction to a multiplicative group modulo 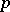 , are uniformizable [6]. The theory of Abelian varieties over global (number and function) fields plays an important role in Diophantine geometry. Its principal result is the Mordell–Weil theorem: The group of rational points of an Abelian variety, defined over a finite extension of the field of rational numbers, is finitely generated.
, are uniformizable [6]. The theory of Abelian varieties over global (number and function) fields plays an important role in Diophantine geometry. Its principal result is the Mordell–Weil theorem: The group of rational points of an Abelian variety, defined over a finite extension of the field of rational numbers, is finitely generated.
References
| [1] | A. Weil, "Courbes algébriques et variétés abéliennes. Variétés abéliennes et courbes algébriques" , Hermann (1971) |
| [2] | A. Weil, "Courbes algébriques et variétés abéliennes. Sur les courbes algébriques et les varietés qui s'en deduisent" , Hermann (1948) |
| [3] | A. Weil, "Introduction à l'Aeetude des variétés kahlériennes" , Hermann (1958) |
| [4] | S. Lang, "Abelian varieties" , Springer (1983) |
| [5] | D. Mumford, "Abelian varieties" , Oxford Univ. Press (1974) |
| [6] | Yu.I. Manin, "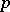 -Adic automorphic functions" J. Soviet Math. , 5 : 3 (1976) pp. 279–333 Itogi Nauk. i Tekhn. Sovrem. Problemy , 3 (1974) pp. 5–93 -Adic automorphic functions" J. Soviet Math. , 5 : 3 (1976) pp. 279–333 Itogi Nauk. i Tekhn. Sovrem. Problemy , 3 (1974) pp. 5–93 |
| [7] | J.-P. Serre, "Groupes algébrique et corps des classes" , Hermann (1959) |
| [8] | C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955) |
Comments
For recent information on the Tate conjectures see [a3]. For the theory of Tate–Honda see also [a4]. Mumford's theory of uniformization is developed in [a1], [a2].
References
| [a1] | D. Mumford, "An analytic construction of degenerating curves over complete local rings" Compos. Math. , 24 (1972) pp. 129–174 |
| [a2] | D. Mumford, "An analytic construction of degenerating Abelian varieties over complete local rings" Compos. Math. , 24 (1972) pp. 239–272 |
| [a3] | G. Faltings, "Endlichkeitssätze für abelsche Varietäten über Zahlkörpern" Invent. Math. , 73 (1983) pp. 349–366 ((Errratum: Invent. Math. 75 (1984), p. 381)) |
| [a4] | J.T. Tate, "Classes d'isogénie des variétés abéliennes sur un corps fini (d' après T. Honda)" , Sem. Bourbaki Exp. 352 , Lect. notes in math. , 179 , Springer (1971) |
Abelian variety. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abelian_variety&oldid=14243