Semi-group of operators

A family $ \{ T \} $ of operators on a Banach space or topological vector space with the property that the composite of any two operators in the family is again a member of the family. If the operators $ T $ are "indexed" by elements of some abstract semi-group $ \mathfrak A $ and the binary operation of the latter is compatible with the composition of operators, $ \{ T \} $ is known as a representation of the semi-group $ \mathfrak A $. The most detailed attention has been given to one-parameter semi-groups (cf. One-parameter semi-group) of bounded linear operators on a Banach space $ X $, which yield a representation of the additive semi-group of all positive real numbers, i.e. families $ T ( t) $ with the property

$$ T ( t + \tau ) x = T ( t) T ( \tau ) x ,\ t , \tau > 0 ,\ x \in X . $$

If $ T ( t) $ is strongly measurable, $ t > 0 $, then $ T ( t) $ is a strongly-continuous semi-group; this will be assumed in the sequel.

The limit

$$ \omega = \lim\limits _ {t \rightarrow \infty } \ t ^ {-1} \mathop{\rm ln} \| T ( t) \| $$

exists; it is known as the type of the semi-group. The functions $ T ( t) x $ increase at most exponentially.

An important characteristic is the infinitesimal operator (infinitesimal generator) of the semi-group:

$$ A _ {0} x = \lim\limits _ {t \rightarrow 0 } t ^ {-1} [ T ( t) x - x ] , $$

defined on the linear set $ D ( A _ {0} ) $ of all elements $ x $ for which the limit exists; the closure, $ A $, of this operator (if it exists) is known as the generating operator, or generator, of the semi-group. Let $ X _ {0} $ be the subspace defined as the closure of the union of all values $ T ( t) x $; then $ D ( A _ {0} ) $ is dense in $ X _ {0} $. If there are no non-zero elements in $ X _ {0} $ such that $ T ( t) x \equiv 0 $, then the generating operator $ A $ exists. In the sequel it will be assumed that $ X _ {0} = X $ and that $ T ( t) x \equiv 0 $ implies $ x = 0 $.

The simplest class of semi-groups, denoted by $ C _ {0} $, is defined by the condition: $ T ( t) x \rightarrow x $ as $ t \rightarrow 0 $ for any $ x \in X $. This is equivalent to the condition: The function $ \| T ( t) \| $ is bounded on any interval $ ( 0 , a ] $. In that case $ T ( t) $ has a generating operator $ A = A _ {0} $ whose resolvent $ R ( \lambda , A ) = ( A - \lambda I ) ^ {-1} $ satisfies the inequalities

$$ \tag{1 } \| R ^ {n} ( \lambda , A ) \| \leq M ( \lambda - \omega ) ^ {-} n ,\ \ n = 1 , 2 , . . . ; \ \lambda > \omega , $$

where $ \omega $ is the type of the semi-group. Conversely, if $ A $ is a closed operator with domain of definition dense in $ X $ and with a resolvent satisfying (1), then it is the generating operator of some semi-group $ T ( t) $ of class $ C _ {0} $ such that $ \| T ( t) \| \leq M e ^ {\omega t } $. Condition (1) is satisfied if

$$ \| R ( \lambda , A ) \| \leq ( \lambda - \omega ) ^ {-1} $$

(the Hill–Yosida condition). If, moreover, $ \omega = 0 $, then $ T ( t) $ is a contraction semi-group: $ \| T ( t) \| \leq 1 $.

A summable semi-group is a semi-group for which the functions $ \| T ( t) x \| $ are summable on any finite interval for all $ x \in X $. A summable semi-group has a generating operator $ A = \overline{ {A _ {0} }}\; $. The operator $ A _ {0} $ is closed if and only if, for every $ x \in X $,

$$ \lim\limits _ {t \rightarrow 0 } \frac{1}{t} \int\limits _ { 0 } ^ { t } T ( s) x d s = x . $$

For $ \mathop{\rm Re} \lambda > \omega $ one can define the Laplace transform of a summable semi-group,

$$ \tag{2 } \int\limits _ { 0 } ^ \infty e ^ {- \lambda t } T ( t) x d t = - R ( \lambda ) x , $$

giving a bounded linear operator $ R ( \lambda ) $ which has many properties of a resolvent operator.

A closed operator $ A $ with domain of definition dense in $ X $ is the generating operator of a summable semi-group $ T ( t) $ if and only if, for some $ \omega $, the resolvent $ R ( \lambda , A ) $ exists for $ \mathop{\rm Re} \lambda > \omega $ and the following conditions hold: a) $ \| R ( \lambda , A ) \| \leq M $, $ \mathop{\rm Re} \lambda > \omega $; b) there exist a non-negative function $ \phi ( t , x ) $, $ t > 0 $, $ x \in X $, jointly continuous in all its variables, and a non-negative function $ \phi ( t) $, bounded on any interval $ [ a , b ] \subset ( 0 , \infty ) $, such that, for $ \omega _ {1} > \omega $,

$$ \int\limits _ { 0 } ^ \infty e ^ {- \omega _ {1} t } \phi ( t , x ) dt < \infty , $$

$$ \overline{\lim\limits}\; _ {t \rightarrow \infty } t ^ {-1} \mathop{\rm ln} \phi ( t) < \infty ,\ \phi ( t , x ) \leq \phi ( t) \| x \| , $$

$$ \| R ^ {n} ( \lambda , A ) x \| \leq \frac{1}{ ( n - 1 ) ! } \int\limits _ { 0 } ^ \infty t ^ {n-1} e ^ {- \lambda t } \phi ( t , x ) dt . $$

Under these conditions

$$ \| T ( t) x \| \leq \phi ( t , x ) ,\ \ \| T ( t) \| \leq \phi ( t) . $$

If one requires in addition that the function $ \| T ( t) \| $ be summable on finite intervals, a necessary and sufficient condition is the existence of a continuous function $ \phi ( t) $ such that, for $ \omega _ {1} > \omega $,

$$ \tag{3 } \int\limits _ { 0 } ^ \infty \phi ( t) e ^ {- \omega _ {1} t } dt < \infty , $$

$$ \tag{4 } \| R ^ {n} ( \lambda , A ) \| \leq \frac{1}{( n - 1 ) ! } \int\limits _ { 0 } ^ \infty t ^ {n-1} e ^ {- \lambda t } \phi ( t) dt , $$

$$ \lambda > \omega ,\ n= 1 , 2 , . . . . $$

Under these conditions, $ \| T ( t) \| \leq \phi ( t) $. By choosing different functions satisfying (3), one can define different subclasses of summable semi-groups. If $ \phi ( t) = Me ^ {\omega t } $, the result is the class $ C _ {0} $ and (1) follows from (4). If $ \phi ( t) = Mt ^ {- \alpha } e ^ {\omega t } $, $ 0 \leq \alpha < 1 $, condition (4) implies the condition

$$ \| R ^ {n} ( \lambda , A ) \| \leq \frac{M \Gamma ( n - \alpha ) }{( n - 1 ) ! ( \lambda - \omega ) ^ {n - \alpha } } ,\ \ \lambda > \omega ,\ n = 1 , 2 ,\dots. $$

Semi-groups with power singularities.

If in the previous example $ \alpha \geq 1 $, then the integrals in (4) are divergent for $ n \leq \alpha - 1 $. Hence the generating operator for the corresponding semi-group may not have a resolvent for any $ \lambda $, i.e. it may have a spectrum equal to the entire complex plane. However, for $ n $ large enough one can define for such operators functions $ S _ {n} ( \lambda , A ) $ which coincide with the functions $ R ^ {n+} 1 ( \lambda , A ) $ in the previous cases. The operator function $ S _ {n} ( \lambda , A ) $ is called a resolvent of order $ n $ if it is analytic in some domain $ G \subset \mathbf C $ and if for $ \lambda \in G $,

$$ S _ {n} ( \lambda , A ) Ax = A S _ {n} ( \lambda , A ) x ,\ \ x \in D ( A) , $$

$$ S _ {n} ( \lambda , A ) ( A - \lambda ) ^ {n+} 1 x = x ,\ x \in D ( A ^ {n+} 1 ) , $$

and if $ S _ {n} ( \lambda , A ) x = 0 $ for all $ \lambda \in G $ implies $ x = 0 $. If $ \overline{D}\; ( A ^ {n+} 1 ) = X $, the operator may have a unique resolvent of order $ n $, for which there is a maximal domain of analyticity, known as the resolvent set of order $ n $.

Let $ T ( t) $ be a strongly-continuous semi-group such that the inequality

$$ \| T ( t) \| \leq M t ^ {- \alpha } e ^ {\omega t } $$

holds for $ \alpha \geq 1 $. Then its generating operator $ B $ has a resolvent of order $ n $ for $ n > \alpha - 1 $, and, moreover,

$$ S _ {n} ( \lambda , B ) x = \ \frac{1}{n!} \int\limits _ { 0 } ^ \infty t ^ {n} e ^ {- \lambda t } T ( t) x dt ,\ \mathop{\rm Re} \lambda > \omega , $$

$$ \tag{5 } \left \| \frac{d ^ {k} S _ {n} ( \lambda , B ) }{d \lambda ^ {k} } x \right \| \leq \frac{M \Gamma ( k + n + 1 - \alpha ) }{n ! ( \mathop{\rm Re} \lambda - \omega ) ^ {k + n + 1 - \alpha } } , $$

$$ \mathop{\rm Re} \lambda > \omega ,\ k = 0 , 1 ,\dots . $$

Conversely, suppose that for $ \mathop{\rm Re} \lambda > 0 $ the operator $ B $ has a resolvent $ S _ {n} ( \lambda , B ) $ of order $ n $ satisfying (5) with $ n > \alpha - 1 $. Then there exists a unique semi-group $ T ( t) $ such that

$$ \| T ( t) \| \leq M t ^ {- \alpha } e ^ {\omega t } , $$

and the generating operator $ A $ of this semi-group is such that $ S _ {n} ( \lambda , A ) = S _ {n} ( \lambda , B ) $.

Smooth semi-groups.

If $ x \in D ( A _ {0} ) $, the function $ T ( t) x $ is continuously differentiable and

$$ \frac{d T ( t) }{dt} x = A _ {0} T ( t) x = T ( t) A _ {0} x . $$

There exist semi-groups of class $ C _ {0} $ such that, if $ x \notin D ( A _ {0} ) = D ( A) $, the functions $ T ( t) x $ are non-differentiable for all $ t $. However, there are important classes of semi-groups for which the degree of smoothness increases with increasing $ t $. If the functions $ T ( t) x $, $ t > t _ {0} $, are differentiable for any $ x \in X $, then it follows from the semi-group property that the $ T ( t) x $ are twice differentiable if $ t > 2 t _ {0} $, three times differentiable if $ t > 3 t _ {0} $, etc. Therefore, if these functions are differentiable at any $ t > 0 $ for $ x \in X $, then $ T ( t) x $ is infinitely differentiable.

Given a semi-group of class $ C _ {0} $, a necessary and sufficient condition for the functions $ T ( t) x $ to be differentiable for all $ x \in X $ and $ t > t _ {0} $, where $ t _ {0} \geq 0 $, is that there exist numbers $ a , b , c > 0 $ such that the resolvent $ R ( \lambda , A ) $ is defined in the domain

$$ \mathop{\rm Re} \lambda > a - b \mathop{\rm ln} | \mathop{\rm Im} \lambda | , $$

while in this domain

$$ \| R( \lambda , A ) \| \leq c | \mathop{\rm Im} \lambda | . $$

A necessary and sufficient condition for $ T ( t) x $ to be infinitely differentiable for all $ x \in X $ and $ t > 0 $ is that, for every $ b > 0 $, there exist $ a _ {b} , c _ {b} $ such that the resolvent $ R ( \lambda , A ) $ is defined in the domain

$$ \mathop{\rm Re} \lambda > a _ {b} - b \mathop{\rm ln} | \mathop{\rm Im} \lambda | , $$

and such that

$$ \| R ( \lambda , A ) \| \leq c _ {b} | \mathop{\rm Im} \lambda | . $$

Sufficient conditions are: If there exists a $ \mu > \omega $ for which

$$ \overline{\lim\limits}\; _ {\tau \rightarrow \infty } \mathop{\rm ln} | \tau | \| R ( \mu + i \tau , A ) \| = t _ {0} < \infty , $$

then the $ T ( t) x $ are differentiable for $ t > t _ {0} $ and $ x \in X $; if $ t _ {0} = 0 $, then the $ T ( t) x $ are infinitely differentiable for all $ t > 0 $ and $ x \in X $.

The degree of smoothness of a semi-group may sometimes be inferred from its behaviour at zero; for example, suppose that for every $ c > 0 $ there exists a $ \delta _ {c} $ such that, for $ 0 < t < \delta _ {c} $,

$$ \| I - T ( t) \| \leq 2 - ct \mathop{\rm ln} t ^ {-1} , $$

then the $ T ( t) x $ are infinitely differentiable for all $ t > 0 $, $ x \in X $.

There are smoothness conditions for summable semi-groups and semi-groups of polynomial growth. If a semi-group has polynomial growth of degree $ \alpha $ and is infinitely differentiable for $ t > 0 $, then the function

$$ \frac{d T ( t) }{dt} x = A T ( t) x $$

also has polynomial growth:

$$ \| A T ( t) \| \leq M _ {1} t ^ {- \beta } e ^ {\omega t } . $$

In the general case there is no rigorous relationship between the numbers $ \alpha $ and $ \beta $, and $ \beta $ can be utilized for a more detailed classification of infinitely-differentiable semi-groups of polynomial growth.

Analytic semi-groups.

An important class of semi-groups, related to partial differential equations of parabolic type, comprises those semi-groups $ T ( t) $ which admit an analytic continuation to some sector of the complex plane containing the positive real axis. A semi-group of class $ C _ {0} $ has this property if and only if its resolvent satisfies the following inequality in some right half-plane $ \mathop{\rm Re} \lambda > \omega $:

$$ \| R ( \lambda , A ) \| \leq M | \lambda - \omega | ^ {-1} . $$

Another necessary and sufficient conditions is: The semi-group is strongly differentiable and its derivative satisfies the estimate

$$ \left \| \frac{d T }{dt} ( t) \right \| \leq M t ^ {-1} e ^ {\omega t } . $$

Finally, the inequality

$$ \overline{\lim\limits}\; _ {t \rightarrow 0 } \| I - T ( t) \| < 2 $$

is also a sufficient condition for $ T ( t) $ to be analytic.

If a semi-group $ T ( t) $ has an analytic continuation $ T ( z) $ to a sector $ | \mathop{\rm arg} z | < \phi \leq \pi / 2 $ and has polynomial growth at zero, $ \| T ( z) \| \leq c | z | ^ \alpha $, $ \alpha > 0 $, then the resolvent $ S _ {n} ( \lambda , A ) $ of order $ n > \alpha - 1 $ of its generating operator $ A $ has an analytic continuation to the sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \phi $, and satisfies the following estimate in any sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \psi $, $ \psi < \phi $:

$$ \| S _ {n} ( \lambda , A ) \| \leq | \lambda | ^ {\alpha - n - 1 } M ( \psi ) . $$

Conversely, suppose that the resolvent $ S _ {n} ( \lambda , B ) $ of an operator $ B $ is defined in a sector $ | \mathop{\rm arg} \lambda | \leq \pi / 2 + \psi $ and that

$$ \| S _ {n} ( \lambda , B ) \| \leq \lambda ^ {\alpha - n - 1 } M . $$

Then there exists a semi-group $ T ( z) $ of growth $ \alpha $, analytic in the sector $ | \mathop{\rm arg} z | < \psi $, whose generating operator $ A $ is such that $ S _ {n} ( \lambda , A ) = S _ {n} ( \lambda , B ) $.

Distribution semi-groups.

In accordance with the general concept of the theory of distributions (cf. Generalized function), one can drop the requirement that the operator-valued function $ T ( t) $ be defined for every $ t > 0 $, demanding only that it be possible to evaluate the integrals $ \int _ {- \infty } ^ {+ \infty } T ( t) \phi ( t) dt $ for all $ \phi $ in the space $ D ( \mathbf R ) $ of infinitely-differentiable functions with compact support. Hence the following definition: A distribution semi-group on a Banach space $ X $ is a continuous linear mapping $ T ( \phi ) $ of $ D ( \mathbf R ) $ into the space $ L ( X) $ of all bounded linear operators on $ X $, with the following properties: a) $ T ( \phi ) = 0 $ if $ \supp \phi \subset ( - \infty , 0 ) $; b) if $ \phi , \psi $ are functions in the subspace $ D ^ {+} ( \mathbf R ) $ of all functions in $ D ( \mathbf R ) $ with support in $ ( 0 , \infty ) $, then $ T ( \phi * \psi ) = T ( \phi ) T ( \psi ) $, where the star denotes convolution:

$$ \phi * \psi = \int\limits _ {- \infty } ^ \infty \phi ( t - s ) \psi ( s) d s $$

(the semi-group property); c) if $ T ( \phi ) x = 0 $ for all $ \phi \in D ^ {+} ( \mathbf R ) $, then $ x = 0 $; d) the linear hull of the set of all values of $ T ( \phi ) x $, $ \phi \in D ^ {+} ( \mathbf R ) $, $ x \in X $, is dense in $ X $; e) for any $ y = T ( \psi ) x $, $ \psi \in D ^ {+} ( \mathbf R ) $, there exists a continuous $ u ( t) $ on $ ( 0 , \infty ) $ with values in $ X $, so that $ u( 0) = y $ and

$$ T ( \phi ) y = \int\limits _ { 0 } ^ \infty \phi ( t) u ( t) dt $$

for all $ \phi \in D ( \mathbf R ) $.

The infinitesimal operator $ A _ {0} $ of a distribution semi-group is defined as follows. If there exists a delta-sequence $ \{ \rho _ {n} \} \subset D ^ {+} ( \mathbf R ) $ such that $ T ( \rho _ {n} ) x \rightarrow x $ and $ T ( - \rho _ {n} ^ \prime ) x \rightarrow y $ as $ n \rightarrow \infty $, then $ x \in D ( A _ {0} ) $ and $ y = A _ {0} x $. The infinitesimal operator has a closure $ A = \overline{ {A _ {0} }}\; $, known as the infinitesimal generator of the distribution semi-group. The set $ \cap_{n=1}^ \infty D ( A _ {0} ^ {n} ) $ is dense in $ X $ and contains $ T ( \phi ) X $ for any $ \phi \in D ^ {+} ( \mathbf R ) $.

A closed linear operator $ A $ with a dense domain of definition in $ X $ is the infinitesimal generator of a distribution semi-group if and only if there exist numbers $ a , b \geq 0 $, $ c > 0 $ and a natural number $ m $ such that the resolvent $ R ( \lambda , A ) $ exists for $ \mathop{\rm Re} \lambda \geq a \mathop{\rm ln} ( 1 + | \lambda | ) + b $ and satisfies the inequality

$$ \tag{6 } \| R ( \lambda , A ) \| \leq c ( 1 + | \lambda | ) ^ {m} . $$

If $ A $ is a closed linear operator on $ X $, then the set $ \cap_{n=1}^ \infty D ( A ^ {n} ) $ can be made into a Fréchet space $ X _ \infty $ by introducing the system of norms

$$ \| x \| _ {n} = \sum_{k=0}^n \| A ^ {k} x \| . $$

The restriction $ A _ \infty $ of $ A $ to $ X _ \infty $ leaves $ X _ \infty $ invariant. If $ A $ is the infinitesimal generator of a semi-group, then $ A _ \infty $ is the infinitesimal generator of a semi-group of class $ C _ {0} $( continuous for $ t \geq 0 $, $ T ( 0 ) = I $) on $ X _ \infty $. Conversely, if $ X _ \infty $ is dense in $ X $, the operator $ A $ has a non-empty resolvent set and $ A $ is the infinitesimal generator of a semi-group of class $ C _ {0} $ on $ X _ \infty $, then $ A $ is the infinitesimal generator of a distribution semi-group on $ X $.

A distribution semi-group has exponential growth of order at most $ q $, $ 1 \leq q < \infty $, if there exists an $ \omega > 0 $ such that $ \mathop{\rm exp} ( - \omega t ^ {q} ) T ( \phi ) $ is a continuous mapping in the topology induced on $ D ^ {+} $ by the space $ S ( \mathbf R ) $ of rapidly-decreasing functions. A closed linear operator is the infinitesimal generator of a distribution semi-group with the above property if and only if it has a resolvent $ R ( \lambda , A ) $ which satisfies (6) in the domain

$$ \{ \lambda : { \mathop{\rm Re} \lambda \geq [ \alpha \mathop{\rm ln} ( 1 + | \mathop{\rm Im} \ \lambda | + \beta ) ] ^ {1- 1/q } , \mathop{\rm Re} \lambda > \omega } \} , $$

where $ \alpha , \beta > 0 $. In particular, if $ q = 1 $ the semi-group is said to be exponential and inequality (6) is valid in some half-plane. There exists a characterization of the semi-groups of the above types in terms of the operator $ A _ \infty $. Questions of smoothness and analyticity have also been investigated for distribution semi-groups.

Semi-groups of operators in a (separable) locally convex space $ X $.

The definition of a strongly-continuous semi-group of operators $ T ( t ) $ continuous on $ X $ remains the same as for a Banach space. Similarly, the class $ C _ {0} $ is defined by the property $ T ( t ) x \rightarrow x $ as $ t \rightarrow 0 $ for any $ x \in X $. A semi-group is said to be locally equicontinuous (of class $ lC _ {0} $) if the family of operators $ T ( t ) $ is equicontinuous when $ t $ ranges over any finite interval in $ ( 0 , \infty ) $. In a barrelled space, a semi-group of class $ C _ {0} $ is always equicontinuous (cf. Equicontinuity).

A semi-group is said to be equicontinuous (of class $ uC _ {0} $) if the family $ T ( t ) $, $ 0 \leq t < \infty $, is equicontinuous.

Infinitesimal operators and infinitesimal generators are defined as in the Banach space case.

Assume from now on that the space $ X $ is sequentially complete. The infinitesimal generator $ A $ of a semi-group of class $ l C _ {0} $ is identical to the infinitesimal operator; its domain of definition, $ D ( A) $, is dense in $ X $ and, moreover, the set $ \cap_{n=1}^ \infty D ( A ^ {n} ) $ is dense in $ X $. The semi-group $ T ( t ) $ leaves $ D ( A) $ invariant and

$$ \frac{dT}{dt} ( t) x = \ AT ( t ) x = T ( t ) Ax ,\ 0 \leq t < \infty ,\ x \in D ( A ) . $$

If $ A $ is the infinitesimal generator of a semi-group of class $ u C _ {0} $, the resolvent $ R ( \lambda , A ) $ is defined for $ \mathop{\rm Re} \lambda > 0 $ and is the Laplace transform of the semi-group.

A linear operator $ A $ is the infinitesimal generator of a semi-group of class $ u C _ {0} $ if and only if it is closed, has dense domain of definition in $ X $, and if there exists a sequence of positive numbers $ \lambda _ {k} \rightarrow \infty $ such that, for any $ \lambda _ {k} $, the resolvent $ R ( \lambda _ {k} , A ) $ is defined and the family of operators $ [ \lambda _ {k} R ( \lambda _ {k} , A ) ] ^ {n} $, $ k , n = 1 , 2 \dots $ is equicontinuous. In this situation the semi-group can be constructed by the formula

$$ ( t ) x = \lim\limits _ {k \rightarrow \infty } \ \left ( \mathop{\rm exp} \left [ - \lambda _ {k} - \lambda _ {k} ^ {2} R ( \lambda _ {k} , A ) \right ] t \right ) x , $$

$$ t \geq 0 ,\ x \in X . $$

In a non-normed locally convex space, the infinitesimal generator of a semi-group of class $ lC _ {0} $ may have no resolvent at any point. An example is: $ A = d / ds $ in the space $ C ^ \infty $ of infinitely-differentiable functions of $ s $ on $ \mathbf R $. As a substitute for the resolvent one can take a continuous operator whose product with $ A - \lambda I $, from the right and the left, differs by a "small amount" from the identity operator.

A continuous operator $ R ( \lambda ) $ defined for $ \lambda $ in a set $ \Lambda \subset \mathbf C $ is called an asymptotic resolvent for a linear operator $ A $ if $ AR ( \lambda ) $ is continuous on $ X $, the operator $ R ( \lambda ) A $ can be extended from $ D ( A) $ to a continuous operator $ B ( \lambda ) $ on $ X $, and if there exists a limit point $ \lambda _ {0} $ of the set $ \Lambda $ such that $ H ^ {+} ( \lambda ) x \rightarrow 0 $, $ H ^ {-} ( \lambda ) x \rightarrow 0 $ as $ \lambda \rightarrow \lambda _ {0} $ for any $ x \in X $, where

$$ H ^ {+} ( \lambda ) = ( A - \lambda I ) R ( \lambda ) - I ,\ \ H ^ {-} ( \lambda ) = B ( \lambda ) - \lambda R ( \lambda ) - I . $$

An asymptotic resolvent possesses various properties resembling those of the ordinary resolvent.

A closed linear operator $ A $ with a dense domain of definition in $ X $ is the infinitesimal generator of a semi-group of class $ l C _ {0} $ if and only if there exist numbers $ \omega $ and $ \alpha > 0 $ such that, for $ \lambda > \omega $, there exists an asymptotic resolvent $ R ( \lambda ) $ of $ A $ with the properties: the functions $ R ( \lambda ) $, $ H ^ {+} ( \lambda ) $, $ H ^ {-} ( \lambda ) $ are strongly infinitely differentiable for $ \lambda > \omega $, and the families of operators

$$ e ^ {\alpha \lambda } \frac{d ^ {n} H ^ \pm ( \lambda ) }{d \lambda ^ {n} } ,\ \frac{\lambda ^ {n+} 1 }{n ! } \frac{d ^ {n} R ( \lambda ) }{d \lambda ^ {n} } ,\ \lambda > \omega ,\ n = 0 , 1 \dots $$

are equicontinuous.

Generation theorems have also been proved for other classes of semi-groups of operators on a locally convex space.

Adjoint semi-groups.

If $ T ( t ) $ is a semi-group of class $ C _ {0} $ on a Banach space $ X $, then the adjoint operators form a semi-group of bounded operators on the adjoint space $ X ^ \prime $. However, the assertion that $ T ^ \prime ( t ) f \rightarrow f $ as $ t \rightarrow 0 $ for any $ f \in X ^ \prime $ is valid only in the sense of the weak- topology $ \sigma ( X ^ \prime , X ) $. If $ A $ is the generating operator, its adjoint $ A ^ \prime $ is a weak infinitesimal generator for $ T ^ \prime ( t ) $, in the sense that $ D ( A ^ \prime ) $ is the set of all $ f $ for which the limit of $ t ^ {-1} [ T ^ \prime ( t ) - I ] f $ as $ t\rightarrow 0 $ exists in the sense of weak- convergence and is equal to $ A ^ \prime f $. The domain of definition $ D ( A ^ \prime ) $ is dense in $ X ^ \prime $— again in the sense of the weak- topology — and the operator $ A ^ \prime $ is closed in the weak- topology.

Let $ X ^ {+} $ be the set of all elements in $ X ^ \prime $ such that $ T ^ \prime ( f ) \rightarrow f $ as $ t \rightarrow 0 $ in the strong sense; then $ X ^ {+} $ is a closed subspace of $ X ^ \prime $ that is invariant under all $ T ^ \prime ( t ) $. On $ X ^ {+} $ the operators $ T ^ \prime ( t ) $ form a semi-group of class $ C _ {0} $. The space $ X ^ {+} $ is also the strong closure of the set $ D ( A ^ \prime ) $ in $ X ^ \prime $. If the original space is reflexive, then $ X ^ {+} = X ^ \prime $. Analogous propositions hold for semi-groups of class $ C _ {0} $ in locally convex spaces. Semi-groups of classes $ l C _ {0} $ and $ u C _ {0} $ generate semi-groups of the same classes in $ X ^ {+} $.

Distribution semi-groups in a (separable) locally convex space.

A distribution semi-group $ T $ in a sequentially complete locally convex space is defined just as in a Banach space. A semi-group $ T $ is said to be locally equicontinuous (of class $ lD ^ \prime $) if, for any compact subset $ K \subset D ( \mathbf R ) $, the family of operators $ \{ T ( \phi ) \} $, $ \phi \in K $, is equicontinuous. In a barrelled space $ X $, any distribution semi-group is defined by analogy to the Banach case. For semi-groups of class $ l D ^ \prime $, the infinitesimal operator is closed $ ( A _ {0} = A ) $, $ \cap_{n=1}^ \infty D ( A ^ {n} ) $ is dense in $ X $, and for any $ x \in X $ and $ \phi \in D ( \mathbf R ) $,

$$ \tag{7 } \left . \begin{array}{c} {T ( \phi ) x \in D ( A ) ,\ T ^ \prime ( \phi ) x = AT ( \phi ) x + \phi ( 0 ) x , } \\ {T ^ \prime ( \phi ) x = T ( \phi ) Ax + \phi ( 0 ) x ,\ x \in D ( A ). } \end{array} \right \} $$

A generalized function $ T $ with support in $ [ 0 , \infty ) $, possessing the properties (7), is naturally called the fundamental function of the operator $ ( d / dt ) - A $. Thus, if $ A $ is the infinitesimal operator of a semi-group $ T $ of class $ l D ^ \prime $, then $ T $ is the fundamental function of the operator $ ( d / dt ) - A $. The converse statement is true under certain additional assumptions about the order of singularity of the fundamental function $ T $( or, more precisely, of the function $ f ( T ( \phi ) x ) $, where $ f \in X ^ \prime $).

A useful notion for the characterization of semi-groups in a locally convex space is that of the generalized resolvent. Let $ \widehat \phi $ denote the Laplace transform of a function $ \phi \in D ( \mathbf R ) $, and let $ \widehat{D} ( \mathbf R ) $ be the space of all such transforms. A topology is induced in this space, via the Laplace transform, from the topology of $ D ( \mathbf R ) $. The Laplace transform of an $ X $- valued generalized function $ F $ is defined by $ \widehat{F} ( \widehat \phi ) = F ( \phi ) $. Under these conditions, $ \widehat{F} $ is a continuous mapping of $ \widehat{D} ( \mathbf R ) $ into the space $ L ( X ) $ of continuous linear operators on $ X $. Let $ \widehat{D} {} _ {+} ^ \prime $ be the space of all $ \widehat{F} $ obtained from functions $ F $ with support in $ ( 0 , \infty ) $, with the natural topology. If $ A $ is a linear operator on $ X $, it can be "lifted" to an operator $ \widetilde{A} $ on $ \widehat{D} {} _ {+} ^ \prime $ via the equality

$$ ( \widetilde{A} \widehat{F} ) = A ( \widehat{F} ( \widehat \phi ) ) = A F ( \phi ) . $$

Thus, it is defined for all $ \widehat{F} \in \widehat{D} {} _ {+} ^ \prime $ such that the right-hand side of the equality is defined for any $ \phi \in D ( \mathbf R ) $ and it extends to a generalized function in $ \widehat{D} {} _ {+} ^ \prime $. The continuous operator $ \widetilde \lambda $ on $ \widehat{D} {} _ {+} ^ \prime $ is defined by

$$ ( \widetilde \lambda \widehat{F} ) ( \widehat \phi ) = \lambda \widehat{F} ( \widehat \phi ) = F ^ \prime ( \phi ) = - F ( \phi ^ \prime ) . $$

If the operator $ \widetilde{A} - \widetilde \lambda $ has a continuous inverse $ \widetilde{R} $ on $ \widehat{D} {} _ {+} ^ \prime $, then $ \widetilde{R} $ is called the generalized resolvent of $ A $.

An operator $ A $ has a generalized resolvent if and only if the operator $ ( d / dt ) - A $ has a locally equicontinuous fundamental function $ T $, constructed by the formula

$$ T ( \phi ) x = ( \widetilde{R} ( 1 \otimes x ) ) ( \widehat \phi ) ,\ \phi \in D ( \mathbf R ) ,\ \ x \in X , $$

where

$$ ( 1 \otimes x ) ( \widehat \phi ) = ( \delta \otimes x ) \phi = \phi ( 0 ) x . $$

Subject to certain additional assumptions, $ T $ is a distribution semi-group. An extension theorem for semi-groups of class $ l C _ {0} $ has also been proved in terms of generalized resolvents.

See also Semi-group of non-linear operators.

References

[1]	E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957) MR0089373 Zbl 0392.46001 Zbl 0033.06501
[2]	Yu.M. Vuvunikyan, "Evolutionary representations of algebras of generalized functions" , Theory of operators in function spaces , Novosibirsk (1977) pp. 99–120 (In Russian)
[3]	P.P. Zabreiko, A.V. Zafievskii, "On a certain class of semigroups" Soviet Math. Dokl. , 10 : 6 (1969) pp. 1523–1526 Dokl. Akad. Nauk SSSR , 189 : 5 (1969) pp. 934–937 MR264459
[4]	A.V. Zafievskii, Trudy Mat. Inst. Voronezh. Univ. , 1 (1970) pp. 206–210
[5]	K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, §1 MR0617913 Zbl 0435.46002
[6]	S.G. Krein, "Linear differential equations in Banach space" , Transl. Math. Monogr. , 29 , Amer. Math. Soc. (1971) (Translated from Russian) MR0342804 Zbl 0179.20701
[7]	Yu.T. Sil'chenko, "An evolutionary equation with an operator generating a nonlinear semigroup" Differential Equations , 15 : 2 (1979) pp. 255–258 Differentsial'nye Uravneniya , 15 : 2 (1979) pp. 363–366 Zbl 0505.34046
[8]	J. Chazarain, "Problèmes de Cauchy abstracts et applications à quelques problèmes mixtes" J. Funct. Anal. , 7 : 3 (1971) pp. 386–446
[9]	I. Ciorânescu, "La caracterisation spectrale d'opérateur, générateurs des semi-groupes distributions d'ordre fini de croissance" J. Math. Anal. Appl. , 34 (1971) pp. 34–41
[10]	I. Ciorânescu, "A characterization of distribution semigroups of finite growth order" Rev. Roum. Math. Pures Appl. , 22 : 8 (1977) pp. 1053–1068 MR500280 Zbl 0374.46032
[11]	T. Kato, "A characterization of holomorphic semigroups" Proc. Amer. Math. Soc. , 25 : 3 (1970) pp. 495–498 MR0264456 Zbl 0199.45604
[12]	J. Lions, "Les semigroupes distributions" Portugal. Math. , 19 (1960) pp. 141–164
[13]	A. Pazy, "On the differentiability and compactness of semi-groups of linear operators" J. Math. Mech. , 17 : 12 (1968) pp. 1131–1141 MR231242 Zbl 0162.45903
[14]	A. Pazy, "Approximations of the identity operator by semigroups of linear operators" Proc. Amer. Math. Soc. , 30 : 1 (1971) pp. 147–150 MR0287362
[15]	T. Ushijima, "On the abstract Cauchy problems and semi-groups of linear operators in locally convex spaces" Sci. Papers College Gen. Educ. Univ. Tokyo , 21 (1971) pp. 93–122 MR0312324 Zbl 0239.47031
[16]	T. Ushijima, "On the generation and smoothness of semi-groups of linear operators" J. Fac. Sci. Univ. Tokyo, Sec. 1A , 19 : 1 (1972) pp. 65–127 MR0308854 Zbl 0239.47032
[17]	C. Wild, "Semi-groupes de croissance 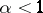holomorphes" C.R. Acad. Sci. Paris Sér. A , 285 (1977) pp. 437–440 (English abstract) MR448159 Zbl 0359.47024
[18]	J.A. Gol'dstein, "Semigroups of linear operators and application" , Oxford Univ. Press (1985) (Translated from Russian)
[19]	A. Pazy, "Semigroups of linear operators and application to partial differential equations" , Springer (1983) MR0710486
[20]	Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , CWI Monographs , 5 , North-Holland (1987) MR0915552 Zbl 0636.47051
[a1]	P. Butzer, H. Berens, "Semigroups of operators and approximation" , Springer (1967) MR230022
[a2]	H. Kellermann, M. Hieber, "Integrated semigroups" J. Funct. Anal. , 84 (1989) pp. 160–180 MR0999494 Zbl 0604.47025
[a3]	I. Miyadera, N. Tanaka, "Exponentially bounded $c$-semigroups and integrated semigroups" Tokyo J. Math. , 12 (1989) pp. 99–115 MR1001735