Semi-group of non-linear operators

A one-parameter family of operators $ S ( t ) $, $ 0 \leq t < \infty $, defined and acting on a closed subset $ G $ of a Banach space $ X $, with the following properties:

1) $ S ( t + \tau ) x = S ( t ) ( S ( \tau ) x ) $ for $ x \in C $, $ t , \tau > 0 $;

2) $ S ( 0 ) x = x $ for any $ x \in C $;

3) for any $ x \in C $, the function $ S ( t ) x $( with values in $ X $) is continuous with respect to $ t $ on $ [ 0 , \infty ) $.

A semi-group $ S ( t ) $ is of type $ \omega $ if

$$ \| S ( t ) x - S ( t ) y \| \leq e ^ {\omega t } \| x - y \| ,\ \ x , y \in C ,\ t> 0 . $$

A semi-group of type $ 0 $ is called a contraction semi-group.

As in the case of semi-groups of linear operators (cf. Semi-group of operators), one introduces the concept of the generating operator (or infinitesimal generator) $ A _ {0} $ of the semi-group $ S ( t ) $:

$$ A _ {0} x = \lim\limits _ {h \rightarrow 0 } \frac{S ( h ) x - x }{h} $$

for those elements $ x \in C $ for which the limit exists. If $ S ( t ) $ is a contraction semi-group, $ A _ {0} $ is a dissipative operator. Recall that an operator $ A $ on a Banach space $ X $ is dissipative if $ \| x - y - \lambda ( Ax - Ay ) \| \geq \| x - y \| $ for $ x , y \in \overline{ {D ( A) }}\; $, $ \lambda > 0 $. A dissipative operator may be multi-valued, in which case $ Ax $ in the definition stands for any of its values at $ x $. A dissipative operator is said to be $ m $- dissipative if $ \mathop{\rm Range} ( I - \lambda A ) = X $ for $ \lambda > 0 $. If $ S ( t ) $ is of type $ \omega $, then $ A _ {0} - \omega I $ is dissipative.

The fundamental theorem on the generation of semi-groups: If $ A - \omega I $ is a dissipative operator and $ \mathop{\rm Range} ( I - \lambda A ) $ contains $ D ( A ) $ for sufficiently small $ \lambda > 0 $, then there exists a semi-group $ S _ {A} ( t ) $ of type $ \omega $ on $ \overline{ {D ( A ) }}\; $ such that

$$ S _ {A} ( t ) x = \lim\limits _ {n \rightarrow \infty } \ \left ( I - \frac{t}{n} A \right ) ^ {-} n x , $$

where $ x \in \overline{ {D ( A ) }}\; $ and the convergence is uniform on any finite $ t $- interval. (The existence of $ S _ {A} ( t ) $ can also be proved if one replaces the condition $ \mathop{\rm Range} ( I - \lambda A ) \supset \overline{ {D ( A ) }}\; $ by the weaker condition

$$ \lim\limits _ {\overline{ {\lambda \downarrow 0 }}\; } \ \lambda ^ {-} 1 d ( \mathop{\rm Range} ( I - \lambda A ) , x ) = 0 , $$

where $ d $ is the distance between sets.)

For any operator $ A $ one has a corresponding Cauchy problem

$$ \tag{* } \frac{du}{dt} ( t) \in Au ( t ) ,\ t > 0 ,\ u ( 0) = x . $$

If the problem (*) has a strong solution, i.e. if there exists a function $ u ( t ) $ which is continuous on $ [ 0 , \infty ) $, absolutely continuous on any compact subset of $ ( 0, \infty ) $, takes values in $ D ( A ) $ for almost all $ t > 0 $, has a strong derivative for almost all $ t > 0 $, and satisfies the relation (*), then $ u ( t ) = S _ {A} ( t ) x $. Any function $ S _ {A} ( t ) x $ is a unique integral solution of the problem (*).

Under the assumptions of the fundamental theorem, if $ X $ is a reflexive space and $ A $ is closed (cf. Closed operator), then the function $ u ( t ) = S _ {A} ( t ) x $ yields a strong solution of the Cauchy problem (*) for $ x \in D ( A) $, with $ ( du / dt) ( t) \in A ^ {0} u ( t ) $ almost everywhere, where $ A ^ {0} z $ is the set of elements of minimal norm in $ Az $. In that case the generating operator $ A _ {0} $ of the semi-group $ S _ {A} ( t ) $ is densely defined: $ \overline{ {D ( A _ {0} ) }}\; = \overline{ {D ( A ) }}\; $. If, moreover, $ X $ and $ X ^ \prime $ are uniformly convex, then the operator $ A ^ {0} $ is single-valued and for all $ t \geq 0 $ there exists a right derivative $ d ^ {+} u / dt = A ^ {0} u ( t ) $; this function is continuous from the right on $ [ 0, \infty ) $, and continuous at all points with the possible exception of a countable set; in this case $ D ( A _ {0} ) = D ( A ) $ and $ A _ {0} = A ^ {0} $.

If $ X $ is reflexive (or $ X = Y ^ \prime $, where $ Y $ is separable) and $ A $ is a single-valued operator and has the property that $ x _ {n} \rightarrow x $ in $ X $ and $ Ax _ {n} \rightarrow y $ in the weak topology $ \sigma ( X , X ^ \prime ) $( respectively, in $ \sigma ( X , Y ) $) imply $ y = Ax $, then $ u ( t) \in D ( A ) $, $ t \geq 0 $, and $ u ( t ) $ is a weakly (weak- $ * $) continuously-differentiable solution of the problem (*). In the non-reflexive case, examples are known where the assumptions of the fundamental theorem hold with $ \overline{ {D ( A) }}\; = X $ and the functions $ u ( t ) = S _ {A} ( t ) x $ do not even have weak derivatives on $ X $ at any $ x \in X $, $ t \geq 0 $.

Let $ A $ be a continuous operator, defined on all of $ X $, such that $ A - \omega I $ is dissipative. Then $ \mathop{\rm Range} ( I - \lambda A ) = X $ for $ \lambda > 0 $, $ \lambda \omega < 1 $, and for any $ x \in X $ the problem (*) has a unique continuously-differentiable solution on $ [ 0 , \infty ) $, given by $ u ( t ) = S _ {A} ( t ) x $. If $ A $ is continuous on its closed domain $ D ( A ) $, then it will be the generating operator of a semi-group of type $ \omega $ on $ D ( A) $ if only and only if $ A - \omega I $ is dissipative and $ \lim\limits _ {\lambda \rightarrow 0 } \lambda ^ {-} 1 d ( x + \lambda Ax , D ( A ) ) = 0 $ for $ x \in D ( A) $.

In a Hilbert space $ H $, a contraction semi-group on a set $ C $ may be extended to a contraction semi-group on a closed convex subset $ \widetilde{C} $ of $ H $. Moreover, the generating operator $ A _ {0} $ of the extended semi-group is defined on a set dense in $ \widetilde{C} $. There exists a unique $ m $- dissipative operator such that $ \overline{ {D ( A) }}\; = C $ and $ A _ {0} = A ^ {0} $. If $ A $ is $ m $- dissipative, then $ \overline{ {D ( A) }}\; $ is convex and there exists a unique contraction semi-group $ S ( t ) = S _ {A} ( t) $ on $ \overline{ {D ( A) }}\; $ such that $ A _ {0} = A ^ {0} $.

Let $ \phi $ be a convex semi-continuous functional defined on a real Hilbert space $ H $ and let $ \partial \phi $ be its subdifferential; then the operator $ Ax = - \partial \phi ( x) $( for all $ x $ such that $ \partial \phi ( x) $ is non-empty) is dissipative. The semi-group $ S _ {A} ( t ) $ possesses properties similar to those of a linear analytic semi-group. In particular, $ S _ {A} ( t) x \in D ( A) $( $ t> 0 $) for any $ x \in \overline{ {D ( A) }}\; $, and $ u ( t ) = S _ {A} ( t) x $ is a strong solution of the Cauchy problem (*), with

$$ \left \| \frac{d ^ {+} u }{dt} ( t) \right \| = \ \| A ^ {0} u ( t ) \| \leq \frac{2}{t} \ \| x - v \| + 2 \| A ^ {0} v \| $$

for all $ t > 0 $, $ v \in D ( A) $. If $ \phi $ attains its minimum, then $ u ( t ) $ converges weakly to some minimum point as $ t \rightarrow \infty $.

Theorems about the approximation of semi-groups play an essential role in the approximate solution of Cauchy problems. Let $ X $, $ X _ {n} $, $ n = 1 , 2 \dots $ be Banach spaces; let $ A $, $ A _ {n} $ be operators defined and single-valued on $ X $, $ X _ {n} $, respectively, satisfying the assumptions of the fundamental theorem for the same type $ \omega $; let $ p _ {n} : X \rightarrow X _ {n} $ be linear operators, $ \| p _ {n} \| _ {X \rightarrow X _ {n} } \leq \textrm{ const } $. Then convergence of the resolvents (cf. Resolvent) ( $ \lambda > 0 $, $ \lambda \omega < 1 $)

$$ \| ( I - \lambda A _ {n} ) ^ {-} 1 p _ {n} x - p _ {n} ( I - \lambda A ) ^ {-} 1 x \| _ {X _ {n} } \rightarrow 0 $$

for $ x \in \overline{ {D ( A) }}\; $ implies convergence of the semi-groups

$$ \| S _ {A _ {n} } ( t) p _ {n} x - p _ {n} S _ {A} ( t) x \| _ {X _ {n} } \rightarrow 0 ,\ x \in \overline{ {D ( A) }}\; , $$

uniformly on any finite closed interval.

The multiplicative formulas developed by S. Lie in the finite-dimensional linear case can be generalized to the non-linear case. If $ A $, $ B $ and $ A + B $ are single-valued $ m $- dissipative operators on a Hilbert space and the closed convex set $ C \subset \overline{ {D ( A) }}\; \cap \overline{ {D ( B) }}\; $ is invariant under $ ( I - \lambda A ) ^ {-} 1 $ and $ ( I - \lambda B ) ^ {-} 1 $, then, for any $ x \in C \cap \overline{ {D ( A) \cap D ( B) }}\; $,

$$ \tag{** } S _ {A + B } ( t) x = \lim\limits _ {n \rightarrow \infty } \ \left [ S _ {A} \left ( \frac{t}{n} \right ) S _ {B} \left ( \frac{t}{n} \right ) \right ] ^ {n} x . $$

This formula is also valid in an arbitrary Banach space $ X $ for any $ x \in X $, provided $ A $ is a densely-defined $ m $- dissipative linear operator and $ B $ is a continuous dissipative operator defined on all of $ X $. In both cases

$$ S _ {A + B } ( t) x = \lim\limits \ \left [ \left ( I - \frac{t}{n} B \right ) ^ {-} 1 \left ( I - \frac{t}{n} A \right ) ^ {-} 1 \right ] ^ {n} x , $$

$$ x \in \overline{ {D ( A) \cap D ( B) }}\; . $$

Examples of non-linear differential operators satisfying the conditions of the fundamental theorem on the generation of semi-groups are given below. In each case only the space $ X $ and the boundary conditions are indicated, while $ D ( A) $ is not described. In all examples, $ \Omega $ is a bounded domain in $ \mathbf R ^ {n} $ with smooth boundary; $ \beta , \gamma $ are multi-valued maximal monotone mappings $ \mathbf R \rightarrow \mathbf R $, $ \beta ( 0) \ni 0 $, $ \gamma ( 0) \ni 0 $; and $ \psi : \mathbf R \rightarrow \mathbf R $ is a continuous strictly-increasing function, $ \psi ( 0) = 0 $.

Example 1.

$ X = L _ {p} ( \Omega ) $, $ 1 \leq p \leq \infty $, $ Au = \Delta u - \beta ( u) $, $ - \partial u / \partial n \in \gamma ( u) $ on $ \Gamma $.

Example 2.

$ X = L _ {1} ( \Omega ) $, $ Au = \Delta \psi ( u) $, $ - \partial u / \partial n \in \gamma ( u) $ on $ \Gamma $.

Example 3.

$ X = W _ {2} ^ {-} 1 ( \Omega ) $, $ Au = \Delta \psi ( u) $, $ u = 0 $ on $ \Gamma $.

Example 4.

$ X = C ( \overline \Omega \; ) $ or $ X = L _ \infty ( \Omega ) $, $ Au = \psi ( \Delta u ) $, $ u = 0 $ on $ \Gamma $.

Example 5.

$ X = L _ {1} ( \mathbf R ^ {n} ) $, $ Au = \mathop{\rm div} f ( u) $, where $ f \in C ^ {1} ( \mathbf R ) $ with values in $ \mathbf R ^ {n} $, $ f ( 0) = 0 $.

Example 6.

$ X = L _ \infty ( \mathbf R ) $, $ Au = f ( u _ {x} ) $, where $ f : \mathbf R \rightarrow \mathbf R $ is continuous.

References

[1]	V. Barbu, "Nonlinear semigroups and differential equations in Banach spaces" , Ed. Academici (1976) (Translated from Rumanian)
[2]	H. Brézis, "Opérateurs maximaux monotones et semigroups de contractions dans les espaces de Hilbert" , North-Holland (1973)
[3]	H. Brézis, A. Pazy, "Convergence and approximation of semigroups of nonlinear operators in Banach spaces" J. Funct. Anal. , 9 : 1 (1972) pp. 63–74
[4]	M.G. Crandall, T.M. Liggett, "Generation of semi-groups of nonlinear transformations on general Banach spaces" Amer. J. Math. , 93 : 2 (1971) pp. 265–298
[5]	Y. Kobayashi, "Difference approximation of Gauchy problems for quasi-dissipative operators and generation of nonlinear semigroups" J. Math. Soc. Japan , 27 : 4 (1975) pp. 640–665
[6]	Y. Konishi, "On the uniform convergence of a finite difference scheme for a nonlinear heat equation" Proc. Japan. Acad. , 48 : 2 (1972) pp. 62–66
[7]	R.H. Martin, "Differential equations on closed subsets of a Banach space" Trans. Amer. Math. Soc. , 179 (1973) pp. 399–414
[8]	G.F. Webb, "Continuous nonlinear perturbations of linear accretive operators in Banach spaces" J. Funct. Anal. , 10 : 2 (1972) pp. 191–203
[9]	M.I. [M.I. Khazan] Hazan, "Nonlinear evolution equations in locally convex spaces" Soviet Math. Dokl. , 14 : 5 (1973) pp. 1608–1614 Dokl. Akad. Nauk SSSR , 212 : 6 (1973) pp. 1309–1312
[10]	M.I. [M.I. Khazan] Hazan, "Differentiability of nonlinear semigroups and the classical solvability of nonlinear boundary value problems for the equation 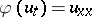" Soviet Math. Dokl. , 17 : 3 (1976) pp. 839–843 Dokl. Akad. Nauk SSSR , 228 : 4 (1976) pp. 805–808

Comments

See also Semi-group of operators; One-parameter semi-group.

The formula (**) above, especially in the form

$$ e ^ {it ( A+ B) } = {s - \lim\limits } _ {n \rightarrow \infty } \ ( e ^ {itA/n } e ^ {itB/n } ) ^ {n} , $$

which holds, e.g., when $ A, B $ are self-adjoint operators on a separable Hilbert space so that $ A+ B $, defined on $ D ( A) \cap D ( B) $, is self-adjoint, is known as the Trotter product formula, [a5], [a4].

References

[a1]	Ph. Clément, H.J.A.M. Heijmans, S. Angenent, C.J. van Duijn, B. de Pagter, "One-parameter semigroups" , CWI Monographs , 5 , North-Holland (1987)
[a2]	A. Pazy, "Semigroups of linear operators and applications to partial differential equations" , Springer (1983)
[a3]	R.H. Martin, "Nonlinear operators and differential equations in Banach spaces" , Wiley (1976)
[a4]	B. Simon, "Functional integration and quantum physics" , Acad. Press (1979) pp. 4–6
[a5]	H. Trotter, "On the product of semigroups of operators" Proc. Amer. Math. Soc. , 10 (1959) pp. 545–551