Elliptic genera

The name elliptic genus has been given to various multiplicative cobordism invariants taking values in a ring of modular forms. The following is an attempt to present the simplest case — level- $ 2 $ genera in characteristic $ \neq 2 $— in a unified way. It is convenient to use N. Katz's approach to modular forms (cf. [a7]) and view a modular form as a function of elliptic curves with a chosen invariant differential (cf. also Elliptic curve). A similar approach to elliptic genera was used by J. Franke [a3].

Jacobi functions.

Let $ K $ be any perfect field of characteristic $ \neq 2 $ and fix an algebraic closure $ {\overline{K}\; } $ of $ K $( cf. Algebraically closed field). Consider a triple $ ( E, \omega, \alpha ) $ consisting of:

i) an elliptic curve $ E $ over $ K $, i.e. a smooth curve of genus $ 1 $ with a specified $ K $- rational base-point $ O $;

ii) an invariant $ K $- rational differential $ \omega $;

iii) a $ K $- rational primitive $ 2 $- division point $ \alpha $. Following J.I. Igusa [a6] (up to a point), one can associate to these data two functions, $ x $ and $ y $, as follows.

The set $ E _ {4} \subset E ( {\overline{K}\; } ) $ of $ 4 $- division points on $ E $ can be described as follows. There are four $ 2 $- division points $ t $( $ \alpha $ is one of them), four primitive $ 4 $- division points $ r $ such that $ 2r = \alpha $, and eight primitive $ 4 $- division points $ s $ such that $ 2s \neq \alpha $. Consider the degree- $ 0 $ divisor $ D = \sum ( t ) - \sum ( r ) $. Since $ \sum t - \sum r = 0 $ in $ E $ and since Galois symmetries transform $ D $ into itself, Abel's theorem (cf., for example, [a11], III.3.5.1, or Abel theorem) implies that there is a function $ x \in K ( E ) ^ \times $, uniquely defined up to a multiplicative constant, such that $ { \mathop{\rm div} } ( x ) = D $.

The function $ x $ is odd, satisfies $ x ( u + \alpha ) \equiv x ( u ) $, and undergoes sign changes under the two other translations of exact order $ 2 $. Moreover, if $ r \in E _ {4} $ satisfies $ 2r = \alpha $, then translation by $ r $ transforms $ x $ into $ Cx ^ {- 1 } $ for some non-zero constant $ C $. This constant depends on the choice of $ r $ but only up to sign. It follows that $ x ^ {2} ( u + r ) x ^ {2} ( u ) $ does not depend on the choice of $ r $. This constant is written as $ \varepsilon ^ {- 1 } $, i.e.

$$ \varepsilon \equiv x ^ {- 2 } ( u + r ) x ^ {- 2 } ( u ) . $$

One also defines

$$ \delta = { \frac{1}{8} } \sum x ^ {- 2 } ( s ) $$

(the summation is over the primitive $ 4 $- division points $ s $ such that $ 2s \neq \alpha $). If $ a $ is one of the values of $ x ( s ) $, the other values are $ \pm a, \pm \varepsilon ^ {- {1 / 2 } } a ^ {- 1 } $, each taken twice. It follows that

$$ \delta = { \frac{1}{2} } ( a ^ {- 2 } + \varepsilon a ^ {2} ) $$

and

$$ \prod ( X - x ( s ) ) = \varepsilon ^ {- 2 } ( 1 - 2 \delta X ^ {2} + \varepsilon X ^ {4} ) ^ {2} = \varepsilon ^ {- 2 } R ( X ) ^ {2} . $$

It is now easy to see that

$$ { \mathop{\rm div} } ( R ( x ) ) = 2 \left ( \sum ( s ) - 2 \sum ( r ) \right ) . $$

Using once more Abel's theorem, one sees that there is a unique $ y \in K ( E ) ^ \times $ such that $ { \mathop{\rm div} } ( y ) = \sum ( s ) - 2 \sum ( r ) $, and $ y ( O ) = 1 $. Since $ x ( O ) = 0 $, one has $ y ^ {2} = R ( x ) $.

The differential $ dx $ has four double poles $ r $. Also, it is easy to see that $ s $ is a double zero of $ x - x ( s ) $, hence a simple zero of $ dx $. One concludes that

$$ { \mathop{\rm div} } ( dx ) = \sum ( s ) - 2 \sum ( r ) = { \mathop{\rm div} } ( y ) . $$

and that $ { {dx } / y } $ is an invariant differential on $ E $.

A slight modification of the argument given in [a6] shows that the Jacobi elliptic functions satisfy the Euler addition formula

$$ x ( u + v ) ( 1 - \varepsilon x ^ {2} ( u ) x ^ {2} ( v ) ) = x ( u ) y ( v ) + x ( v ) y ( u ) . $$

Accordingly, one defines the Euler formal group law $ F ( U,V ) \in K [ [ U,V ] ] $ by

$$ F ( U,V ) = { \frac{U \sqrt {R ( V ) } + V \sqrt {R ( U ) } }{1 - \varepsilon U ^ {2} V ^ {2} } } . $$

Notice that since $ { \mathop{\rm char} } K \neq 2 $, $ F ( U,V ) $ is defined over $ K $.

The elliptic genus.

At this point, one normalizes $ x $ over $ K $ by requiring that $ { {dx } / y } = \omega $( the given invariant differential). All the objects $ x, y, \delta, \varepsilon $, and $ F ( U,V ) $ are now completely determined by the initial data. Replacing $ \omega $ by $ \lambda \omega $( $ \lambda \in K ^ \times $) yields:

$$ \tag{a1 } x \asR \lambda x, \quad y \asR y, \quad \delta \asR \lambda ^ {- 2 } \delta, $$

$$ \varepsilon \asR \lambda ^ {- 4 } \varepsilon, \quad F ( U,V ) \asR \lambda F ( \lambda ^ {- 1 } U, \lambda ^ {- 1 } V ) . $$

As any formal group law, $ F ( U,V ) $ is classified by a unique ring homomorphism

$$ \psi : {\Omega _ {*} ^ { { \mathop{\rm U} } } } \rightarrow K $$

from the complex cobordism ring. Since $ F ( - U, - V ) = - F ( U,V ) $, it is easy to see that $ \psi $ uniquely factors through a ring homomorphism

$$ \varphi : {\Omega _ {*} ^ { { \mathop{\rm SO} } } } \rightarrow K $$

from the oriented cobordism ring. By definition, $ \varphi $ is the level- $ 2 $ elliptic genus. Suppose now that $ { \mathop{\rm char} } K = 0 $. Define a local parameter $ z $ near $ O $ so that $ z ( O ) = 0 $ and $ dz = \omega $. Then $ x $ can be expanded into a formal power series $ x ( z ) \in K [ [ z ] ] $ which clearly satisfies $ x ( z ) = z + o ( z ) $ and $ x ( - z ) = - x ( z ) $. In this case, the elliptic genus can be defined as the Hirzebruch genus (cf. [a4] or [a5]) corresponding to the series $ P ( z ) = {z / {x ( z ) } } $. Since $ { {d x ( z ) } / {dz } } = y ( z ) $, the logarithm $ g ( z ) $ of this elliptic genus is given by the elliptic integral

$$ \tag{a2 } g ( z ) = \int\limits _ { 0 } ^ { z } { \frac{dt }{\sqrt {1 - 2 \delta t ^ {2} + \varepsilon t ^ {4} } } } , $$

which gives the original definition in [a9].

Modularity.

For any closed oriented manifold $ M $ of dimension $ 4k $, $ \varphi ( M ) $ is a function of the triple $ ( E, \omega, \alpha ) $. As easily follows from (a1), multiplying $ \omega $ by $ \lambda $ results in multiplying $ \varphi ( M ) $ by $ \lambda ^ {- 2k } $. Also, $ \varphi ( M ) $ depends only on the isomorphism class of the triple $ ( E, \omega, \alpha ) $ and commutes with arbitrary extensions of the scalar field $ K $. In the terminology of Katz ([a7]; adapted here to modular forms over fields), $ \varphi ( M ) $ is a modular form of level $ 2 $ and weight $ 2k $. Let $ {\mathcal M} _ {*} $ be the graded ring of all such modular forms. Then $ \varphi ( M ) \in {\mathcal M} _ {2k } $, $ \delta \in {\mathcal M} _ {2} $, $ \varepsilon \in {\mathcal M} _ {4} $. Moreover, one can prove that $ {\mathcal M} _ {*} \cong \mathbf Z [ {1 / 2 } , \delta, \varepsilon ] $. If one identifies these two isomorphic rings, the elliptic genus becomes the Hirzebruch genus

$$ \varphi : {\Omega _ {*} ^ { { \mathop{\rm SO} } } } \rightarrow {\mathbf Z [ {1 / 2 } , \delta, \varepsilon ] } $$

with logarithm given by the formal integral (a2).

Integrality.

Consider

$$ { {\widetilde \varphi } } : {\Omega _ {*} ^ { { \mathop{\rm Spin} } } } \rightarrow { {\mathcal M} _ {*} } , $$

i.e., the composition of $ \varphi $ with the forgetful homomorphism $ \Omega _ {*} ^ { { \mathop{\rm Spin} } } \rightarrow \Omega _ {*} ^ { { \mathop{\rm SO} } } $. As is shown in [a2],

$$ {\widetilde \varphi } ( \Omega _ {*} ^ { { \mathop{\rm Spin} } } ) = \mathbf Z [ 8 \delta, \varepsilon ] . $$

The ring $ \mathbf Z [ 8 \delta, \varepsilon ] $ agrees with the ring $ {\mathcal M} _ {*} ( \mathbf Z ) $ of modular forms over $ \mathbf Z $. Thus: If $ M $ is a $ { \mathop{\rm Spin} } $- manifold of dimension $ 4k $, then $ \varphi ( M ) \in {\mathcal M} _ {2k } ( \mathbf Z ) $.

Example: the Tate curve.

Let $ K $ be a local field, complete with respect to a discrete valuation $ v $, and let $ q \in K ^ \times $ be any element satisfying $ v ( q ) < 0 $. Consider $ E = K ^ \times /q ^ {2 \mathbf Z } $. It is well-known (cf. [a11], § C.14) that $ E $ can be identified with the elliptic curve (known as the Tate curve)

$$ E _ {q ^ {2} } : Y ^ {2} + XY = X ^ {3} + a _ {4} X + a _ {6} , $$

where

$$ a _ {4} = \sum _ {m \geq 1 } ( - 5m ^ {3} ) { \frac{q ^ {2m } }{1 - q ^ {2m } } } , $$

$$ a _ {6} = \sum _ {m \geq 1 } \left ( - { \frac{5m ^ {3} + 7m ^ {5} }{12 } } \right ) { \frac{q ^ {2m } }{1 - q ^ {2m } } } . $$

$ E $ can be treated as an elliptic curve over $ K $ with $ O = 1 $. Fix the invariant differential $ \omega = { {du } / u } $( $ u \in K ^ \times $) on $ E $( $ \omega $ corresponds to the differential $ \omega _ {\textrm{ can } } = { {dX } / {( 2Y + X ) } } $ on the Tate curve). $ E $ has three $ K $- rational primitive $ 2 $- division points: $ - 1 $, $ q $ and $ - q $. To describe the corresponding Jacobi function $ x $, consider the theta-function

$$ \Theta ( u ) = ( 1 - u ^ {- 2 } ) \prod _ {n > 0 } ( 1 - q ^ {2n } u ^ {- 2 } ) ( 1 - q ^ {2n } u ^ {2} ) . $$

This is a "holomorphic" function on $ K ^ \times $ with simple zeros at points of $ \pm q ^ {\mathbf Z} $( cf. [a10] for a justification of this terminology), satisfying

$$ \Theta ( - u ) = \Theta ( u ) , \quad \Theta ( q ^ {- 1 } u ) = - u ^ {2} \Theta ( u ) . $$

Consider the case where $ \alpha = - 1 $. Let $ i \in {\overline{K}\; } $ be any square root of $ - 1 $, and let

$$ \tag{a3 } f ( u ) = { \frac{\Theta ( u ) }{\Theta ( iu ) } } = $$

$$ = { \frac{u ^ {2} - 1 }{u ^ {2} + 1 } } \prod _ {n > 0 } { \frac{( 1 - q ^ {2n } u ^ {- 2 } ) ( 1 - q ^ {2n } u ^ {2} ) }{( 1 + q ^ {2n } u ^ {- 2 } ) ( 1 + q ^ {2n } u ^ {2} ) } } . $$

$ f $ is a meromorphic function on $ E $ satisfying $ f ( iu ) = {1 / {f ( u ) } } $ and

$$ { \mathop{\rm div} } ( f ) = ( 1 ) + ( - 1 ) + ( q ) + ( - q ) + $$

$$ - ( i ) - ( - i ) - ( iq ) - ( - iq ) , $$

i.e., $ f $ is a multiple of the Jacobi function $ x $ of $ ( E, \omega, - 1 ) $.

Notice now that the normalization condition $ { {du } / u } = { {dx } / y } $ can be written as $ y ( u ) = ux ^ \prime ( u ) $, where $ x ^ \prime ( u ) $ is the derivative with respect to $ u $. Since $ y ( 1 ) = 0 $, one has $ x ^ \prime ( 1 ) = 1 $. Differentiating (a3), one obtains

$$ f ^ \prime ( 1 ) = \prod _ {n > 0 } \left ( { \frac{1 - q ^ {2n } }{1 + q ^ {2n } } } \right ) ^ {2} , $$

$$ x ( u ) = { \frac{u ^ {2} - 1 }{u ^ {2} + 1 } } \prod _ {n > 0 } { \frac{( 1 - q ^ {2n } u ^ {- 2 } ) ( 1 - q ^ {2n } u ^ {2} ) ( 1 + q ^ {2n } ) ^ {2} }{( 1 + q ^ {2n } u ^ {- 2 } ) ( 1 + q ^ {2n } u ^ {2} ) ( 1 - q ^ {2n } ) ^ {2} } } , $$

and

$$ \varepsilon = \prod _ {n > 0 } \left ( { \frac{1 - q ^ {2n } }{1 + q ^ {2n } } } \right ) ^ {8} . $$

Finally, if $ { \mathop{\rm char} } K = 0 $, the function $ z = { \mathop{\rm log} } u $ satisfies $ dz = { {du } / u } $. It follows that the generating series $ P ( z ) = {z / {x ( z ) } } $ is given by

$$ P ( z ) = $$

$$ = { \frac{z}{ { \mathop{\rm tanh} } z } } \prod _ {n > 0 } { \frac{( 1 + q ^ {2n } e ^ {- 2z } ) ( 1 + q ^ {2n } e ^ {2z } ) ( 1 - q ^ {2n } ) ^ {2} }{( 1 - q ^ {2n } e ^ {- 2z } ) ( 1 - q ^ {2n } e ^ {2z } ) ( 1 + q ^ {2n } ) ^ {2} } } . $$

The cases where $ \alpha = q $ or $ \alpha = - q $ are treated similarly, with

$$ f ( u ) = { \frac{u \Theta ( u ) }{\Theta ( q ^ {- 1/2 } u ) } } $$

and

$$ f ( u ) = { \frac{u \Theta ( u ) }{\Theta ( iq ^ {- 1/2 } u ) } } , $$

respectively.

Strict multiplicativity.

The following theorem, also known (in an equivalent form) as the Witten conjecture, was proven first by C. Taubes [a12], then by R. Bott and Taubes [a1]. Let $ P $ be a principal $ G $- bundle (cf. also Principal $ G $- object) over an oriented manifold $ B $, where $ G $ is a compact connected Lie group, and suppose $ G $ acts on a compact $ { \mathop{\rm Spin} } $- manifold $ M $. Then

$$ \varphi ( P \times _ {G} M ) = \varphi ( B ) \varphi ( M ) . $$

For the history of this conjecture, cf. [a8].

References

[a1]	R. Bott, C. Taubes, "On the rigidity theorems of Witten" J. Amer. Math. Soc. , 2 (1989) pp. 137–186 MR0954493 Zbl 0667.57009
[a2]	D.V. Chudnovsky, G.V. Chudnovsky, P.S. Landweber, S. Ochanine, R.E. Stong, "Integrality and divisibility of the elliptic genus" Preprint (1988)
[a3]	J. Franke, "On the construction of elliptic cohomology" Math. Nachr. , 158 (1992) pp. 43–65 MR1235295 Zbl 0777.55003
[a4]	F. Hirzebruch, "Topological methods in algebraic geometry" , Grundlehren math. Wiss. , Springer (1966) (Edition: Third) MR0202713 Zbl 0138.42001
[a5]	F. Hirzebruch, Th. Berger, R. Jung, "Manifolds and modular forms" , Aspects of Mathematics , E20 , Vieweg (1992) (Appendices by Nils-Peter Skoruppa and by Paul Baum) MR1189136 Zbl 0752.57013 Zbl 0767.57014
[a6]	J.-I. Igusa, "On the transformation theory of elliptic functions" Amer. J. Math. , 81 (1959) pp. 436–452 MR0104668 Zbl 0131.28102
[a7]	N.M. Katz, "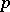-adic properties of modular schemes and modular forms" W. Kuyk (ed.) J.-P. Serre (ed.) , Modular Functions in One Variable III. Proc. Internat. Summer School, Univ. of Antwerp, RUCA, July 17--August 3, 1972 , Lecture Notes in Mathematics , 350 (1973) pp. 69–190 MR0447119 Zbl 0271.10033
[a8]	P.S. Landweber, "Elliptic genera: An introductory overview" P.S. Landweber (ed.) , Elliptic Curves and Modular Forms in Algebraic Topology (Proc., Princeton 1986) , Lecture Notes in Mathematics , 1326 , Springer (1988) pp. 1–10 MR0970279 Zbl 0649.57021
[a9]	S. Ochanine, "Sur les genres multiplicatifs définis par des intégrales elliptiques" Topology , 26 (1987) pp. 143–151 MR0895567 Zbl 0626.57014
[a10]	P. Roquette, "Analytic theory of elliptic functions over local fields" , Hamburger Math. Einzelschrift. , 1 , Vandenhoeck and Ruprecht (1970) MR0260753 Zbl 0194.52002
[a11]	J.H. Silverman, "The arithmetic of elliptic curves" , GTM , 106 , Springer (1986) MR0817210 Zbl 0585.14026
[a12]	C. Taubes, "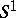 actions and elliptic genera" Comm. Math. Phys. , 122 (1989) pp. 455–526 MR0998662 Zbl 0683.58043