Disconjugacy
2020 Mathematics Subject Classification: Primary: 34L [MSN][ZBL]
An $ n $ th order homogeneous linear differential operator (equation)
$$ \tag{a1 } Ly \equiv y ^ {( n ) } + p _ {1} ( x ) y ^ {( n - 1 ) } + \dots + p _ {n} ( x ) y = 0 $$
is called disconjugate on an interval $ I $ if no non-trivial solution has $ n $ zeros on $ I $, multiple zeros being counted according to their multiplicity. (In the Russian literature this is called non-oscillation on $ I $; cf. also Oscillating solution; Oscillating differential equation.) If (a1) has a solution with $ n $ zeros on an interval, then the infimum of all values $ c $, $ c > a $, such that some solution has $ n $ zeros on $ [ a,c ] $ is called the conjugate point of $ a $ and is denoted by $ \eta ( a ) $. This infimum is achieved by a solution which has a total of at least $ n $ zeros at $ a $ and $ \eta ( a ) $ and is positive on $ ( a, \eta ( a ) ) $. If the equation has continuous coefficients, the conjugate point $ \eta ( a ) $ is a strictly increasing, continuous function of $ a $. The adjoint equation has the same conjugate point as (a1). For general properties, see [a1], [a7].
There are numerous explicit sufficient criteria for the equation (a1) to be disconjugate. Many of them are of the form
$$ \sum ^ {n _ {k} = 1 } c _ {k} ( b - a ) ^ {k} \left \| {p _ {k} } \right \| < 1, $$
where $ \| {p _ {k} } \| $ is some norm of $ p _ {k} $, $ I = [ a,b ] $ and $ c _ {k} $ are suitable constants. These are "smallness conditions" which express the proximity of (a1) to the disconjugate equation $ y ^ {( n ) } = 0 $. See [a12].
$ L $ is disconjugate on $ [ a,b ] $ if and only if it has there the Pólya factorization
$$ Ly \equiv \rho _ {n} { \frac{d}{dx } } \left ( \rho _ {n - 1 } \dots { \frac{d}{dx } } \left ( \rho _ {1} { \frac{d}{dx } } ( \rho _ {0} y ) \right ) \dots \right ) , \rho _ {i} > 0, $$
or the equivalent Mammana factorization
$$ Ly = \left ( { \frac{d}{dx } } + r _ {n} \right ) \dots \left ( { \frac{d}{dx } } + r _ {1} \right ) y. $$
Among the various Pólya factorizations, the most important is the Trench canonical form [a11]: If $ L $ is disconjugate on $ ( a,b ) $, $ b \leq \infty $, then there is essentially one factorization such that $ \int ^ {b} {\rho _ {i} ^ {- 1 } } = \infty $, $ i = 1 \dots n - 1 $.
Disconjugacy is closely related to solvability of the de la Vallée-Poussin multiple-point problem $ Ly = g $, $ y ^ {( i ) } ( x _ {j} ) = a _ {ij } $, $ i = 0 \dots r _ {j} - 1 $, $ \sum _ {1} ^ {m} r _ {j} = n $. The Green's function of a disconjugate operator $ L $ and the related homogeneous boundary value problem satisfies
$$ { \frac{G ( x,t ) }{( x - x _ {1} ) ^ {r _ {1} } \dots ( x - x _ {m} ) ^ {r _ {m} } } } > 0 $$
for $ x _ {1} \leq x \leq x _ {m} $, $ x _ {1} < t < x _ {m} $[a7]. Another interesting boundary value problem is the focal boundary value problem $ y ^ {( i ) } ( x _ {j} ) = 0 $, $ i = r _ {j - 1 } \dots r _ {j} - 1 $, $ j = 1 \dots m $, $ 0 = r _ {0} < r _ {1} < \dots < r _ {m} = n - 1 $.
For a second-order equation, the Sturm separation theorem (cf. Sturm theorem) yields that non-oscillation (i.e., no solution has a sequence of zeros converging to $ + \infty $) implies that there exists a point $ a $ such that (a1) is disconjugate on $ [ a, \infty ) $. For equations of order $ n > 2 $ this conclusion holds for a class of equations [a2] but not for all equations [a4].
Particular results about disconjugacy exist for various special types of differential equations.
1) The Sturm–Liouville operator (cf. Sturm–Liouville equation)
$$ \tag{a2 } ( p y ^ \prime ) ^ \prime + q y = 0, p > 0, $$
has been studied using the Sturm (and Sturm–Picone) comparison theorem, the Prüfer transformation and the Riccati equation $ z ^ \prime + q + { {z ^ {2} } / p } = 0 $. It is also closely related to the positive definiteness of the quadratic functional $ \int _ {a} ^ {b} {( p y ^ {\prime 2 } - q y ^ {2} ) } $. See [a10], [a1], [a5]. For example, (a2) is disconjugate on $ [ a,b ] $ if $ \int _ {a} ^ {b} {p ^ {- 1 } } \times \int _ {a} ^ {b} {| q | } < 4 $.
2) Third-order equations are studied in [a3].
3) For a self-adjoint differential equation $ \sum _ {i = 0 } ^ {m} ( p _ {m - i } y ^ {( i ) } ) ^ {( i ) } = 0 $, the existence of a solution with two zeros of multiplicity $ m $ has been studied. Their absence is called $ ( m,m ) $- disconjugacy.
4) Disconjugacy of the analytic equation $ w ^ \prime + p ( z ) w = 0 $ in a complex domain is connected to the theory of univalent functions. See [a8], [a5] and Univalent function.
5) Many particularly elegant result are available for two-term equations $ y ^ {( n ) } + p ( x ) y = 0 $ and their generalizations $ Ly + p ( x ) y = 0 $[a6], [a2].
Disconjugacy has also been studied for certain second-order linear differential systems of higher dimension [a1], [a9]. In the historical prologue of [a9], the connection to the calculus of variations (cf. also Variational calculus) is explained. The concepts of disconjugacy and oscillation have also been generalized to non-linear differential equations and functional-differential equations.
References
| [a1] | W.A. Coppel, "Disconjugacy" , Lecture Notes in Mathematics , 220 , Springer (1971) |
| [a2] | U. Elias, "Oscillation theory of two-term differential equations" , Kluwer Acad. Publ. (1997) |
| [a3] | M. Gregus, "Third order linear differential equations" , Reidel (1987) |
| [a4] | Gustafson, G. B., "The nonequivalence of oscillation and nondisconjugacy" Proc. Amer. Math. Soc. , 25 (1970) pp. 254–260 |
| [a5] | E. Hille, "Lectures on ordinary differential equations" , Addison-Wesley (1968) |
| [a6] | I.T. Kiguradze, T.A. Chanturia, "Asymptotic properties of solutions of nonautonomous ordinary differential equations" , Kluwer Acad. Publ. (1993) (In Russian) |
| [a7] | A.Yu. Levin, "Non-oscillation of solutions of the equation 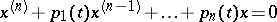 " Russian Math. Surveys , 24 (1969) pp. 43–99 (In Russian) " Russian Math. Surveys , 24 (1969) pp. 43–99 (In Russian) |
| [a8] | Z. Nehari, "The Schwarzian derivative and schlicht functions" Bull. Amer. Math. Soc. , 55 (1949) pp. 545–551 |
| [a9] | W.T. Reid, "Sturmian theory for ordinary differential equations" , Springer (1980) |
| [a10] | C.A. Swanson, "Comparison and oscillatory theory of linear differential equations" , Acad. Press (1968) |
| [a11] | W.F. Trench, "Canonical forms and principal systems for general disconjugate equation" Trans. Amer. Math. Soc. , 189 (1974) pp. 319–327 |
| [a12] | D. Willet, "Generalized de la Vallée Poussin disconjugacy tests for linear differential equations" Canadian Math. Bull. , 14 (1971) pp. 419–428 |
Disconjugacy. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Disconjugacy&oldid=34876