Oscillating differential equation
An ordinary differential equation which has at least one oscillating solution. There are different concepts of the oscillation of a solution. The most widespread are oscillation at a point (usually taken to be $ + \infty $)
and oscillation on an interval. A non-zero solution of the equation
$$ \tag{1 } u ^ {(} n) = f( t, u , u ^ \prime \dots u ^ {(} n- 1) ),\ n \geq 2 , $$
where $ f( t, 0 \dots 0) = 0 $, is called oscillating at the point $ + \infty $( or on an interval $ I $) if it has a sequence of zeros which converges to $ + \infty $( respectively, there are at least $ n $ zeros in $ I $ counted according to their multiplicity). Equation (1) is oscillating at $ + \infty $ or on an interval $ I $ if its solutions are oscillating (at $ + \infty $, respectively, on $ I $).
Among equations which are oscillatory at $ + \infty $ the equations which possess the properties $ A $ or $ B $, i.e. which are compatible in a specific sense with one of the equations
$$ u ^ {(} n) = - u \ \textrm{ or } \ u ^ {(} n) = u , $$
are distinguished. Equation (1) is said to possess property $ A $ if all its solutions defined in a neighbourhood of $ + \infty $ are oscillating when $ n $ is even; when $ n $ is odd, they should either be oscillating or satisfy the condition
$$ \tag{2 } \lim\limits _ {t \rightarrow + \infty } u ^ {(} i- 1) ( t) = 0,\ i = 1 \dots n. $$
If every solution of equation (1) defined in a neighbourhood of $ + \infty $, when $ n $ is even, is either oscillating, or satisfies condition (2) or
$$ \tag{3 } \lim\limits _ {t \rightarrow + \infty } | u ^ {(} i- 1) ( t) | = + \infty ,\ \ i = 1 \dots n, $$
while when $ n $ is odd, it is either oscillating or satisfies condition (3), then the equation possesses property $ B $.
The linear equation
$$ \tag{4 } u ^ {(} n) = a( t) u $$
with a locally summable coefficient $ a: [ t _ {0} , + \infty ) \rightarrow \mathbf R $ possesses property $ A $( property $ B $) if
$$ a( t) \leq 0 \ ( a( t) \geq 0) \ \textrm{ when } t \geq t _ {0} $$
and either
$$ \int\limits _ {t _ {0} } ^ { {+ } \infty } t ^ {n- 1- \epsilon } | a( t) | dt = + \infty $$
or
$$ a( t) \leq \frac{\mu _ {n} - \epsilon }{t ^ {n} } \ \left ( a( t) \geq \frac{\nu _ {n} + \epsilon }{t ^ {n} } \right ) $$
when $ t \geq t _ {0} $, where $ \epsilon > 0 $ and $ \mu _ {n} $ is the smallest ( $ \nu _ {n} $ is the largest) of the local minima (maxima) of the polynomial $ x( x- 1) \dots ( x- n+ 1) $( see [1]–[5]).
An equation of Emden–Fowler type
$$ \tag{5 } u ^ {(} n) = a( t) | u | ^ \lambda \mathop{\rm sign} u ,\ \ \lambda > 0,\ \lambda \neq 1, $$
with a locally summable non-positive (non-negative) coefficient $ a: [ t _ {0} , + \infty ) \rightarrow \mathbf R $ possesses property $ A $( property $ B $) if and only if
$$ \int\limits _ {t _ {0} } ^ { {+ } \infty } t ^ \mu | a( t) | dt = + \infty , $$
where $ \mu = \min \{ n- 1, ( n- 1) \lambda \} $( see [4], [6], [7]).
In a number of cases the question of the oscillation of equation (1) can be reduced to the same question for the standard equations of the form (4) and (5) using a comparison theorem (see [11]).
In studying the oscillatory properties of equations with deviating argument, certain specific features arise. For example, if $ n $ is odd, $ \Delta > 0 $, and if for large $ t $ the inequality
$$ a( t) \leq a _ {0} < - n! \Delta ^ {-} n $$
is fulfilled, then all non-zero solutions of the equation
$$ u ^ {(} n) ( t) = a( t) u( t - \Delta ) $$
are oscillatory at $ + \infty $( see [10], [11]). At the same time, if $ a $ is non-positive and $ n $ is odd, the non-retarded equation (4) always has a non-oscillating solution.
The concepts of oscillation and non-oscillation on an interval are generally studied for linear homogeneous equations. They are of fundamental value in the theory of boundary value problems (see [12]).
References
| [1] | A. Kneser, "Untersuchungen über die reellen Nullstellen der Integrale linearer Integralgleichungen" Math. Ann. , 42 (1893) pp. 409–435 |
| [2] | J.G. Mikusinksi, "On Fite's oscillation theorems" Colloq. Math. , 2 (1951) pp. 34–39 |
| [3] | V.A. Kondrat'ev, "The oscillatory character of solutions of the equation 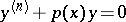 " Trudy Moskov. Mat. Obshch. , 10 (1961) pp. 419–436 (In Russian) " Trudy Moskov. Mat. Obshch. , 10 (1961) pp. 419–436 (In Russian) |
| [4] | I.T. Kiguradze, "On the oscillatory character of solutions of the equation 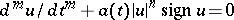 " Mat. Sb. , 65 : 2 (1964) pp. 172–187 (In Russian) " Mat. Sb. , 65 : 2 (1964) pp. 172–187 (In Russian) |
| [5] | T.A. Chanturiya, "On a comparison theorem for linear differential equations" Math. USSR Izv. , 10 : 5 (1976) pp. 1075–1088 Izv. Akad. Nauk. SSSR Ser. Mat. , 40 : 5 (1976) pp. 1128–1142 |
| [6] | I. Ličko, M. Švec, "La charactère oscillatoire des solutions de l'équation  , , 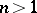 " Chekhosl. Mat. Zh. , 13 (1963) pp. 481–491 " Chekhosl. Mat. Zh. , 13 (1963) pp. 481–491 |
| [7] | I.T. Kiguradze, "On the oscillatory and monotone solutions of ordinary differential equations" Arch. Math. , 14 : 1 (1978) pp. 21–44 |
| [8] | C.A. Swanson, "Comparison and oscillation theory of linear differential equations" , Acad. Press (1968) |
| [9] | P. Hartman, "Ordinary differential equations" , Birkhäuser (1982) |
| [10] | A.D. Myshkis, "Linear differential equations with retarded argument" , Moscow (1972) (In Russian) |
| [11] | R.G. Koplatadze, T.A. Chanturiya, "On the oscillatory properties of differential equations with deviating argument" , Tbilisi (1977) (In Russian) |
| [12] | A.Yu. Levin, "Non-oscillation of the solutions of the equation 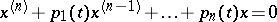 " Russian Math. Surveys , 24 : 2 (1969) pp. 43–99 Uspekhi Mat. Nauk , 24 : 2 (1969) pp. 43–96 " Russian Math. Surveys , 24 : 2 (1969) pp. 43–99 Uspekhi Mat. Nauk , 24 : 2 (1969) pp. 43–96 |
Comments
References
| [a1] | J.K. Hale, "Ordinary differential equations" , Wiley (1969) |
| [a2] | W.T. Reid, "Sturmian theory for ordinary differential equations" , Springer (1980) |
Oscillating differential equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Oscillating_differential_equation&oldid=48083