Difference between revisions of "Regularization of sequences"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
(fix tex) |
||
| Line 14: | Line 14: | ||
$ n = 0, 1 \dots $ | $ n = 0, 1 \dots $ | ||
be a sequence of real numbers (indexed by the non-negative integers). A regularization of $ \{ a _ {n} \} $ | be a sequence of real numbers (indexed by the non-negative integers). A regularization of $ \{ a _ {n} \} $ | ||
| − | is a sequence $ \{ a _ {n} ^ {( | + | is a sequence $ \{ a _ {n} ^ {( r)} \} $ |
obtained from $ \{ a _ {n} \} $ | obtained from $ \{ a _ {n} \} $ | ||
by replacing certain $ a _ {n} $ | by replacing certain $ a _ {n} $ | ||
| Line 20: | Line 20: | ||
functions; that is, the problem of when two sequences of constants determine the same [[Quasi-analytic class|quasi-analytic class]] of functions. The answers tend to be given in the form that the two sequences $ \{ M _ {n} \} $ | functions; that is, the problem of when two sequences of constants determine the same [[Quasi-analytic class|quasi-analytic class]] of functions. The answers tend to be given in the form that the two sequences $ \{ M _ {n} \} $ | ||
and $ \{ L _ {n} \} $ | and $ \{ L _ {n} \} $ | ||
| − | determine the same quasi-analytic class if suitably regularized sequences $ \{ M _ {n} ^ {( | + | determine the same quasi-analytic class if suitably regularized sequences $ \{ M _ {n} ^ {( r)} \} $ |
| − | and $ \{ L _ {n} ^ {( | + | and $ \{ L _ {n} ^ {( r)} \} $ |
are the same, cf. [[#References|[a1]]], [[#References|[a2]]]. | are the same, cf. [[#References|[a1]]], [[#References|[a2]]]. | ||
| Line 31: | Line 31: | ||
a _ {i} \leq | a _ {i} \leq | ||
\frac{i- r }{s- r } | \frac{i- r }{s- r } | ||
| − | a _ {s} + | + | a _ {s} + |
| − | \frac{i}{s-} | + | \frac{s-i}{s-r} a _ {r} ; |
| − | |||
$$ | $$ | ||
that is, if the point $ ( i, a _ {i} ) $ | that is, if the point $ ( i, a _ {i} ) $ | ||
is located below or on the segment in the plane joining $ ( r, a _ {r} ) $ | is located below or on the segment in the plane joining $ ( r, a _ {r} ) $ | ||
| − | and $ ( s, a _ {s} ) $( | + | and $ ( s, a _ {s} ) $ (cf. [[Convex function (of a real variable)|Convex function (of a real variable)]]). |
| − | cf. [[Convex function (of a real variable)|Convex function (of a real variable)]]). | ||
| − | The convex regularization, or Newton regularization, $ \{ a _ {n} ^ {( | + | The convex regularization, or Newton regularization, $ \{ a _ {n} ^ {( c)} \} $ |
of $ \{ a _ {n} \} $ | of $ \{ a _ {n} \} $ | ||
| − | is the largest convex minorant of $ \{ a _ {n} \} $( | + | is the largest convex minorant of $ \{ a _ {n} \} $ (cf. [[Majorant and minorant|Majorant and minorant]], 1)). |
| − | cf. [[Majorant and minorant|Majorant and minorant]], 1)). | ||
The log-convex regularization, or convex regularization by means of the logarithm, of a sequence of positive numbers $ \{ a _ {n} \} $ | The log-convex regularization, or convex regularization by means of the logarithm, of a sequence of positive numbers $ \{ a _ {n} \} $ | ||
| − | is the sequence of positive numbers $ \{ a _ {n} ^ {( | + | is the sequence of positive numbers $ \{ a _ {n} ^ {( lc)} \} $ |
| − | such that $ \{ \mathop{\rm log} a _ {n} ^ {( | + | such that $ \{ \mathop{\rm log} a _ {n} ^ {( lc)} \} $ |
is the convex regularization of $ \{ \mathop{\rm log} a _ {n} \} $. | is the convex regularization of $ \{ \mathop{\rm log} a _ {n} \} $. | ||
It is defined by the relations | It is defined by the relations | ||
$$ | $$ | ||
| − | T _ {a} ( r) = \sup _ { n> } | + | T _ {a} ( r) = \sup _ { n>0 } |
\frac{r ^ {n} }{a _ {n} } | \frac{r ^ {n} }{a _ {n} } | ||
,\ \ | ,\ \ | ||
| − | a _ {n} ^ {( | + | a _ {n} ^ {( lc)} = \sup _ { r>0 } |
\frac{r ^ {n} }{T _ {a} ( r) } | \frac{r ^ {n} }{T _ {a} ( r) } | ||
. | . | ||
$$ | $$ | ||
| − | The exponential regularization $ \{ a _ {n} ^ {( | + | The exponential regularization $ \{ a _ {n} ^ {( e)} \} $ |
of $ \{ a _ {n} \} $ | of $ \{ a _ {n} \} $ | ||
is defined by the relations | is defined by the relations | ||
| Line 69: | Line 66: | ||
\frac{r ^ {n} }{a _ {n} } | \frac{r ^ {n} }{a _ {n} } | ||
\ ( r \geq 1) ,\ \ | \ ( r \geq 1) ,\ \ | ||
| − | a _ {n} ^ {( | + | a _ {n} ^ {( e)} = \sup _ {r \geq n } |
\frac{r ^ {n} | \frac{r ^ {n} | ||
}{S _ {a} ( r) } | }{S _ {a} ( r) } | ||
| Line 76: | Line 73: | ||
The Newton regularization of a sequence $ \{ a _ {n} \} $ | The Newton regularization of a sequence $ \{ a _ {n} \} $ | ||
| − | is very much related to the Newton polygon of $ \{ a _ {n} \} $( | + | is very much related to the Newton polygon of $ \{ a _ {n} \} $ |
| − | this explains the name "Newton regularization" , cf. also [[Newton diagram|Newton diagram]], which discusses the context in which the Newton polygon first arose). For a finite sequence $ \{ a _ {n} \} _ {n=} | + | (this explains the name "Newton regularization" , cf. also [[Newton diagram|Newton diagram]], which discusses the context in which the Newton polygon first arose). For a finite sequence $ \{ a _ {n} \} _ {n=0} ^ {N} $, |
its Newton polygon is the highest convex polygonal line in $ \mathbf R ^ {2} $ | its Newton polygon is the highest convex polygonal line in $ \mathbf R ^ {2} $ | ||
joining $ ( 0, a _ {0} ) $ | joining $ ( 0, a _ {0} ) $ | ||
to $ ( N, a _ {N} ) $, | to $ ( N, a _ {N} ) $, | ||
| − | i.e. it is the polygonal line consisting of the segments joining $ ( i, a _ {i} ^ {( | + | i.e. it is the polygonal line consisting of the segments joining $ ( i, a _ {i} ^ {( c)} ) $ |
| − | to $ ( i+ 1 , a _ {i+} | + | to $ ( i+ 1 , a _ {i+ 1} ^ {( c)} ) $, |
$ i= 0 \dots N- 1 $. | $ i= 0 \dots N- 1 $. | ||
| − | Thus, the number $ a _ {i} ^ {( | + | Thus, the number $ a _ {i} ^ {( c)} $ |
is the ordinate of the point of the Newton polygon of $ \{ a _ {i} \} $ | is the ordinate of the point of the Newton polygon of $ \{ a _ {i} \} $ | ||
with abscissa $ i $. | with abscissa $ i $. | ||
| Line 97: | Line 94: | ||
Figure: r080940a | Figure: r080940a | ||
| − | To avoid certain pathologies (like $ a _ {i} ^ {( | + | To avoid certain pathologies (like $ a _ {i} ^ {( c)} = - \infty $ |
for all $ i > 0 $), | for all $ i > 0 $), | ||
| − | let $ \{ a _ {n} \} _ {n=} | + | let $ \{ a _ {n} \} _ {n=0} ^ \infty $ |
| − | be bounded from below. The Newton polygon of this sequence is defined as the limit of the Newton polygons of the finite sequences $ \{ a _ {n} \} _ {n=} | + | be bounded from below. The Newton polygon of this sequence is defined as the limit of the Newton polygons of the finite sequences $ \{ a _ {n} \} _ {n=0} ^ {N} $ |
as $ N \rightarrow \infty $. | as $ N \rightarrow \infty $. | ||
| − | It remains true that $ a _ {i} ^ {( | + | It remains true that $ a _ {i} ^ {( c)} $ |
| − | is determined by the condition that $ ( i, a _ {i} ^ {( | + | is determined by the condition that $ ( i, a _ {i} ^ {( c)} ) $ |
| − | lies on the Newton polygon of $ \{ a _ {n} \} _ {n=} | + | lies on the Newton polygon of $ \{ a _ {n} \} _ {n=0} ^ \infty $. |
Let $ K $ | Let $ K $ | ||
| − | be a non-Archimedean valued field with [[Valuation|valuation]] $ v $( | + | be a non-Archimedean valued field with [[Valuation|valuation]] $ v $ |
| − | cf. also [[Norm on a field|Norm on a field]]). Let $ 1+ a _ {1} X + \dots + a _ {N} X ^ {N} = f( X) $ | + | (cf. also [[Norm on a field|Norm on a field]]). Let $ 1+ a _ {1} X + \dots + a _ {N} X ^ {N} = f( X) $ |
be a polynomial of degree $ N $ | be a polynomial of degree $ N $ | ||
over $ K $. | over $ K $. | ||
The Newton polygon of the polynomial $ f( X) $ | The Newton polygon of the polynomial $ f( X) $ | ||
is the Newton polygon of the sequence $ ( v( 1), v( a _ {1} ) \dots v ( a _ {N} )) $. | is the Newton polygon of the sequence $ ( v( 1), v( a _ {1} ) \dots v ( a _ {N} )) $. | ||
| − | It carries immediate information on the valuations of the roots of $ f( X) $( | + | It carries immediate information on the valuations of the roots of $ f( X) $ |
| − | in a complete algebraic closure of $ K $). | + | (in a complete algebraic closure of $ K $). |
Indeed, if $ \lambda $ | Indeed, if $ \lambda $ | ||
is the slope of a segment of the Newton polygon of (abscissa) length $ r $, | is the slope of a segment of the Newton polygon of (abscissa) length $ r $, | ||
then there are precisely $ r $ | then there are precisely $ r $ | ||
| − | roots of valuation $ - \lambda $( | + | roots of valuation $ - \lambda $ |
| − | counted with multiplicities); an analogous result holds for roots of power series (this is related to a $ p $- | + | (counted with multiplicities); an analogous result holds for roots of power series (this is related to a $ p $-adic Weierstrass preparation theorem, cf. (the editorial comments to) [[Weierstrass theorem|Weierstrass theorem]], and [[#References|[a3]]]). |
| − | adic Weierstrass preparation theorem, cf. (the editorial comments to) [[Weierstrass theorem|Weierstrass theorem]], and [[#References|[a3]]]). | ||
The Newton polygon of a sequence $ \{ a _ {n} \} $ | The Newton polygon of a sequence $ \{ a _ {n} \} $ | ||
| Line 137: | Line 133: | ||
$$ | $$ | ||
| − | \ | + | \bigcap _ {A \subset U( t,c) } U( t, c). |
$$ | $$ | ||
| Line 154: | Line 150: | ||
$$ | $$ | ||
| − | \ | + | \bigcap _ {A \subset U ^ \omega ( t,c) } U ^ \omega ( t, c) |
$$ | $$ | ||
| − | now defines the $ \omega $- | + | now defines the $ \omega $-regularized sequence $ \{ a _ {n} ^ {( \omega ) } \} $. |
| − | regularized sequence $ \{ a _ {n} ^ {( \omega ) } \} $. | ||
Newton and exponential regularization correspond to $ \omega ( t) \equiv \infty $ | Newton and exponential regularization correspond to $ \omega ( t) \equiv \infty $ | ||
and $ \omega ( t) = \mathop{\rm exp} ( t) $, | and $ \omega ( t) = \mathop{\rm exp} ( t) $, | ||
| Line 164: | Line 159: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Mandelbrojt, "Séries adhérentes, régularisations des suites, applications" , Gauthier-Villars (1952)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.A. Siddigi, "On the equivalence of classes of infinitely differentiable functions" ''Soviet J. Contemp. Math. Anal. Arm. Acad. Sci.'' , '''19''' : 1 (1984) pp. 18–29 ''Izv. Akad. Nauk Arm.SSR Mat.'' , '''19''' : 1 (1984) pp. 19–30</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> N. Koblitz, " | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> S. Mandelbrojt, "Séries adhérentes, régularisations des suites, applications" , Gauthier-Villars (1952)</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> J.A. Siddigi, "On the equivalence of classes of infinitely differentiable functions" ''Soviet J. Contemp. Math. Anal. Arm. Acad. Sci.'' , '''19''' : 1 (1984) pp. 18–29 ''Izv. Akad. Nauk Arm.SSR Mat.'' , '''19''' : 1 (1984) pp. 19–30</TD></TR> | ||
| + | <TR><TD valign="top">[a3]</TD> <TD valign="top"> N. Koblitz, "$p$-adic numbers, $p$-adic analysis, and zeta-functions" , Springer (1977) pp. Chapt. IV, §3–4</TD></TR> | ||
| + | </table> | ||
Latest revision as of 12:49, 12 March 2021
Let $ a _ {n} $,
$ n = 0, 1 \dots $
be a sequence of real numbers (indexed by the non-negative integers). A regularization of $ \{ a _ {n} \} $
is a sequence $ \{ a _ {n} ^ {( r)} \} $
obtained from $ \{ a _ {n} \} $
by replacing certain $ a _ {n} $
which are "excessively high" with respect to the others by suitable lower values. An important application of regularized sequences is to the problem of equivalence of classes of $ C ^ \infty $-
functions; that is, the problem of when two sequences of constants determine the same quasi-analytic class of functions. The answers tend to be given in the form that the two sequences $ \{ M _ {n} \} $
and $ \{ L _ {n} \} $
determine the same quasi-analytic class if suitably regularized sequences $ \{ M _ {n} ^ {( r)} \} $
and $ \{ L _ {n} ^ {( r)} \} $
are the same, cf. [a1], [a2].
Some important regularization procedures are as follows. A sequence $ \{ a _ {n} \} $ of real numbers is called a convex sequence if the function $ n \mapsto a _ {n} $ is convex, i.e. if for all $ 0\leq r < i < s $,
$$ a _ {i} \leq \frac{i- r }{s- r } a _ {s} + \frac{s-i}{s-r} a _ {r} ; $$
that is, if the point $ ( i, a _ {i} ) $ is located below or on the segment in the plane joining $ ( r, a _ {r} ) $ and $ ( s, a _ {s} ) $ (cf. Convex function (of a real variable)).
The convex regularization, or Newton regularization, $ \{ a _ {n} ^ {( c)} \} $ of $ \{ a _ {n} \} $ is the largest convex minorant of $ \{ a _ {n} \} $ (cf. Majorant and minorant, 1)).
The log-convex regularization, or convex regularization by means of the logarithm, of a sequence of positive numbers $ \{ a _ {n} \} $ is the sequence of positive numbers $ \{ a _ {n} ^ {( lc)} \} $ such that $ \{ \mathop{\rm log} a _ {n} ^ {( lc)} \} $ is the convex regularization of $ \{ \mathop{\rm log} a _ {n} \} $. It is defined by the relations
$$ T _ {a} ( r) = \sup _ { n>0 } \frac{r ^ {n} }{a _ {n} } ,\ \ a _ {n} ^ {( lc)} = \sup _ { r>0 } \frac{r ^ {n} }{T _ {a} ( r) } . $$
The exponential regularization $ \{ a _ {n} ^ {( e)} \} $ of $ \{ a _ {n} \} $ is defined by the relations
$$ S _ {a} ( r) = = \max _ {n \leq r } \frac{r ^ {n} }{a _ {n} } \ ( r \geq 1) ,\ \ a _ {n} ^ {( e)} = \sup _ {r \geq n } \frac{r ^ {n} }{S _ {a} ( r) } . $$
The Newton regularization of a sequence $ \{ a _ {n} \} $ is very much related to the Newton polygon of $ \{ a _ {n} \} $ (this explains the name "Newton regularization" , cf. also Newton diagram, which discusses the context in which the Newton polygon first arose). For a finite sequence $ \{ a _ {n} \} _ {n=0} ^ {N} $, its Newton polygon is the highest convex polygonal line in $ \mathbf R ^ {2} $ joining $ ( 0, a _ {0} ) $ to $ ( N, a _ {N} ) $, i.e. it is the polygonal line consisting of the segments joining $ ( i, a _ {i} ^ {( c)} ) $ to $ ( i+ 1 , a _ {i+ 1} ^ {( c)} ) $, $ i= 0 \dots N- 1 $. Thus, the number $ a _ {i} ^ {( c)} $ is the ordinate of the point of the Newton polygon of $ \{ a _ {i} \} $ with abscissa $ i $.
An example of this for the sequence $ ( 1, 1, - 2, 1, - 4/3, 1/3, 0) $, $ N= 6 $, with convex regularization $ ( 1, - 1/2, - 2, - 5/3, - 4/3, - 2/3, 0) $, is given in Fig. a.
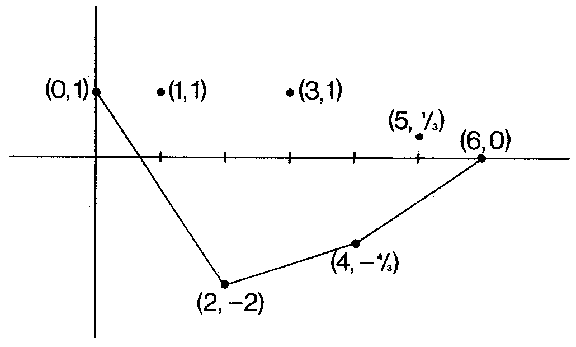
Figure: r080940a
To avoid certain pathologies (like $ a _ {i} ^ {( c)} = - \infty $ for all $ i > 0 $), let $ \{ a _ {n} \} _ {n=0} ^ \infty $ be bounded from below. The Newton polygon of this sequence is defined as the limit of the Newton polygons of the finite sequences $ \{ a _ {n} \} _ {n=0} ^ {N} $ as $ N \rightarrow \infty $. It remains true that $ a _ {i} ^ {( c)} $ is determined by the condition that $ ( i, a _ {i} ^ {( c)} ) $ lies on the Newton polygon of $ \{ a _ {n} \} _ {n=0} ^ \infty $.
Let $ K $ be a non-Archimedean valued field with valuation $ v $ (cf. also Norm on a field). Let $ 1+ a _ {1} X + \dots + a _ {N} X ^ {N} = f( X) $ be a polynomial of degree $ N $ over $ K $. The Newton polygon of the polynomial $ f( X) $ is the Newton polygon of the sequence $ ( v( 1), v( a _ {1} ) \dots v ( a _ {N} )) $. It carries immediate information on the valuations of the roots of $ f( X) $ (in a complete algebraic closure of $ K $). Indeed, if $ \lambda $ is the slope of a segment of the Newton polygon of (abscissa) length $ r $, then there are precisely $ r $ roots of valuation $ - \lambda $ (counted with multiplicities); an analogous result holds for roots of power series (this is related to a $ p $-adic Weierstrass preparation theorem, cf. (the editorial comments to) Weierstrass theorem, and [a3]).
The Newton polygon of a sequence $ \{ a _ {n} \} $ can be obtained geometrically as follows. For all $ t, c \in ( - \infty , \infty ) $ one considers the line $ l( t, c) $ in $ \mathbf R ^ {2} $ through $ ( 0, c) $ of slope $ t $; it is given by the equation $ y= tx+ c $. Let $ U( t, c)= \{ {( x, y) } : {x\geq 0, y\geq tx+ c } \} $ be the supergraph of $ l( t, c) $. Let $ A $ be the graph of $ \{ a _ {n} \} $, $ A= \{ {( i, a _ {i} ) } : {i= 0 , 1 ,\dots } \} $. Then the Newton polygon is the lower boundary of the convex set
$$ \bigcap _ {A \subset U( t,c) } U( t, c). $$
As noted, the Newton regularization (convex regularization) of a sequence $ \{ a _ {n} \} $ is determined by its Newton polygon. This construction has been generalized. Let $ \omega ( t) $ be a non-decreasing function of $ t $ with values in $ [ 0, \infty ] $. Let
$$ U ^ \omega ( t, c) = U( t, c) \cup \{ {( x, y) } : {x > \omega ( t) } \} . $$
The lower boundary of
$$ \bigcap _ {A \subset U ^ \omega ( t,c) } U ^ \omega ( t, c) $$
now defines the $ \omega $-regularized sequence $ \{ a _ {n} ^ {( \omega ) } \} $. Newton and exponential regularization correspond to $ \omega ( t) \equiv \infty $ and $ \omega ( t) = \mathop{\rm exp} ( t) $, respectively.
References
| [a1] | S. Mandelbrojt, "Séries adhérentes, régularisations des suites, applications" , Gauthier-Villars (1952) |
| [a2] | J.A. Siddigi, "On the equivalence of classes of infinitely differentiable functions" Soviet J. Contemp. Math. Anal. Arm. Acad. Sci. , 19 : 1 (1984) pp. 18–29 Izv. Akad. Nauk Arm.SSR Mat. , 19 : 1 (1984) pp. 19–30 |
| [a3] | N. Koblitz, "$p$-adic numbers, $p$-adic analysis, and zeta-functions" , Springer (1977) pp. Chapt. IV, §3–4 |
Regularization of sequences. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regularization_of_sequences&oldid=51698