Difference between revisions of "Jones-Conway polynomial"
Ulf Rehmann (talk | contribs) m (moved Jones–Conway polynomial to Jones-Conway polynomial: ascii title) |
m (AUTOMATIC EDIT (latexlist): Replaced 145 formulas out of 147 by TEX code with an average confidence of 2.0 and a minimal confidence of 2.0.) |
||
| Line 1: | Line 1: | ||
| + | <!--This article has been texified automatically. Since there was no Nroff source code for this article, | ||
| + | the semi-automatic procedure described at https://encyclopediaofmath.org/wiki/User:Maximilian_Janisch/latexlist | ||
| + | was used. | ||
| + | If the TeX and formula formatting is correct, please remove this message and the {{TEX|semi-auto}} category. | ||
| + | |||
| + | Out of 147 formulas, 145 were replaced by TEX code.--> | ||
| + | |||
| + | {{TEX|semi-auto}}{{TEX|partial}} | ||
''Homfly polynomial, Homflypt polynomial, skein polynomial'' | ''Homfly polynomial, Homflypt polynomial, skein polynomial'' | ||
An invariant of oriented links. | An invariant of oriented links. | ||
| − | It is a Laurent polynomial of two variables associated to ambient isotopy classes of oriented links in | + | It is a Laurent polynomial of two variables associated to ambient isotopy classes of oriented links in $\mathbf{R} ^ { 3 }$ (or $S ^ { 3 }$), constructed in 1984 by several groups of researchers (thus the acronyms Homfly and Homflypt) [[#References|[a4]]], [[#References|[a3]]], [[#References|[a14]]], [[#References|[a21]]], and denoted by $P _ { L } ( \square )$. It generalizes the [[Alexander–Conway polynomial|Alexander–Conway polynomial]] and the Jones polynomial. |
There are several constructions of the polynomial, using diagrams of links (and Reidemeister moves, cf. also [[Reidemeister theorem|Reidemeister theorem]]), the braid group (and the Alexander and Markov theorems, cf. also [[Braid theory|Braid theory]]; [[Alexander theorem on braids|Alexander theorem on braids]]; [[Markov braid theorem|Markov braid theorem]]), or statistical mechanics (interpreting the polynomial as a state sum, cf. also [[Statistical mechanics, mathematical problems in|Statistical mechanics, mathematical problems in]]). | There are several constructions of the polynomial, using diagrams of links (and Reidemeister moves, cf. also [[Reidemeister theorem|Reidemeister theorem]]), the braid group (and the Alexander and Markov theorems, cf. also [[Braid theory|Braid theory]]; [[Alexander theorem on braids|Alexander theorem on braids]]; [[Markov braid theorem|Markov braid theorem]]), or statistical mechanics (interpreting the polynomial as a state sum, cf. also [[Statistical mechanics, mathematical problems in|Statistical mechanics, mathematical problems in]]). | ||
| Line 9: | Line 17: | ||
The first approach uses the recursive (skein) relation | The first approach uses the recursive (skein) relation | ||
| − | + | \begin{equation*} v ^ { - 1 } P _ { L _ { + } } ( v , z ) - v P _ { L_- } ( v , z ) = z P _ { L _ { 0 } } ( v , z ), \end{equation*} | |
| − | where | + | where $L _ { + }$, $L_{-}$ and $L_0$ form a [[Conway skein triple|Conway skein triple]]. The Jones–Conway polynomial is usually normalized to be $1$ for the trivial knot. Then for the trivial link of $n$ components, $T _ { n }$, one gets |
| − | + | \begin{equation*} P _ { T _ { n } } ( v , z ) = \left( \frac { v ^ { - 1 } - v } { z } \right) ^ { n - 1 }. \end{equation*} | |
| − | Setting | + | Setting $v = t$ and $z = \sqrt { t } - 1 / \sqrt { t }$ yields the Jones polynomial, $V _ { L } ( t )$, and substituting $v = 1$ and $z = \sqrt { t } - 1 / \sqrt { t }$ yields the [[Alexander–Conway polynomial|Alexander–Conway polynomial]]. |
In the second approach one considers the Hecke algebra associated to the Artin braid group and constructs on it the Jones–Ocneanu trace, which essentially is invariant under Markov moves. This approach is strongly related to the first approach, as the Hecke algebra quadratic relation is analogous to the skein relation of the first method. | In the second approach one considers the Hecke algebra associated to the Artin braid group and constructs on it the Jones–Ocneanu trace, which essentially is invariant under Markov moves. This approach is strongly related to the first approach, as the Hecke algebra quadratic relation is analogous to the skein relation of the first method. | ||
| Line 24: | Line 32: | ||
| − | 1) | + | 1) $P _ { L } ( v , z )$ is an element of the Laurent polynomial ring $\mathbf{Z} [ v ^ { \pm 1 } , z ^ { \pm 1 } ]$. Furthermore, $( v z ) ^ { \operatorname { com } ( L ) - 1 } P _ { L } ( v , z ) \in \mathbf{Z} [ v ^ { \pm 2 } , z ^ { 2 } ]$, where $\operatorname { com}( L )$ denotes the number of components of $L$. In particular, |
| − | + | \begin{equation*} P _ { L } ( v , z ) = P _ { L } ( - v , - z ) = ( - 1 ) ^ { \operatorname { com } ( L ) - 1 } P _ { L } ( - v , z ). \end{equation*} | |
| − | For example, for the right-handed Hopf link, | + | For example, for the right-handed Hopf link, $2_{1}$, one has |
| − | + | \begin{equation*} P _ { 2 _ { 1 } } = \frac { v - v ^ { 3 } } { z } + v z. \end{equation*} | |
| − | 2) If | + | 2) If $\bar{L}$ denotes the mirror image of a link $L$, then |
| − | + | \begin{equation*} P _ { \overline{L} } ( v , z ) = P _ { L } ( - v ^ { - 1 } , z ). \end{equation*} | |
| − | This property often allows one to detect lack of amphicheirality of a link. For example, for the right-handed trefoil knot, | + | This property often allows one to detect lack of amphicheirality of a link. For example, for the right-handed trefoil knot, $3_1$, one has $P _ { 3_1 } = 2 v ^ { 2 } - v ^ { 4 } + v ^ { 2 } z ^ { 2 }$, so the trefoil knot is not amphicheiral. For the figure eight knot, $4_1$, which is amphicheiral, one gets $P _ { 4 _ { 1 } } = v ^ { - 2 } - 1 + v ^ { 2 } - z ^ { 2 }$. The first non-amphicheiral knot not detected by the Jones–Conway polynomial is the $9_{42}$ knot. The [[Kauffman polynomial|Kauffman polynomial]] also does not detect non-amphicheirality of $9_{42}$. However, one can use the Jones–Conway polynomial of the $2$-cable of $9_{42}$ to see that it is non-amphicheiral. |
3) Next, | 3) Next, | ||
| − | <table class="eq" style="width:100%;"> <tr><td | + | <table class="eq" style="width:100%;"> <tr><td style="width:94%;text-align:center;" valign="top"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/j/j130/j130040/j13004036.png"/></td> </tr></table> |
| − | where | + | where $\#$ denotes the [[Connected sum|connected sum]] and $\cup$ the split sum of links. Because the connected sum of links may depend on the choice of connected components, one can use the connected sum formula to find different links with the same Jones–Conway polynomial, for example the connected sum of three Hopf links can give two different results, both with the polynomial equal to $( ( v - v ^ { 3 } ) / z + v z ) ^ { 3 }$. |
| − | 4) If | + | 4) If $L^-$ denotes the link obtained by reversing the orientation of $L$, then the Jones–Conway polynomials of $L$ and $L^-$ coincide. Thus, each non-reversible knot ($8 _ { 17 }$ is the smallest example) gives rise to an example of different knots with the same Jones–Conway polynomial. Furthermore, if $K _ { 1 }$ and $K _ { 2 }$ are two non-reversible knots, then $K _ { 1 } \# K _ { 2 }$ and $K _ { 1 } \# K _ { 2 } ^ { - }$ are different knots which cannot be distinguished by the Jones–Conway polynomials (nor by the Kauffman polynomials) of their satellites. It is an open problem (as of 2001) whether they can be distinguished by any Vassiliev–Gusarov invariants. |
| − | If | + | If $P _ { L } ( v , z ) = \sum _ { i = m } ^ { M } P _ { i } ( v ) z ^ { i }$ (with $P _ { m } ( v ) \neq 0$, $P _ { M } ( v ) \neq 0$), then $m = 1 - \operatorname { com } ( L )$ and $M \leq \operatorname { cr } ( D _ { L } ) - s ( D _ { L } ) + 1$, where $D_{ L}$ is any diagram of $L$, $\operatorname { cr } ( D _ { L } )$ denotes the number of crossings of $D_{ L}$ and $s ( D _ { L } )$ is the number of Seifert circles of $D_{ L}$. The equality holds, e.g., for homogeneous diagrams (including positive and alternating diagrams). In particular for a non-trivial knot $K$, $M < \text{cr} ( K )$ where $\operatorname { cr } ( K )$ is the crossing number of $K$, i.e. the minimum over all diagrams of $L$ of the crossing number. |
| − | 5) If | + | 5) If $\varphi ( D ) = \operatorname { cr } ( D _ { L } ) - s ( D _ { L } ) + 1$, then |
| − | + | \begin{equation*} P _ { \varphi ( D _ { 1 } * D _ { 2 } )} ( v ) = P _ { \varphi ( D _ { 1 } )} ( v ) P _ { \varphi ( D _ { 2 } )} ( v ), \end{equation*} | |
| − | where | + | where $D _ { 1 } * D _ { 2 }$ denotes the planar star (Murasugi) product of the diagrams $D _ { 1 }$ and $D _ { 2 }$ [[#References|[a15]]]. D.L. Vertigan proved that for a fixed $i$, $P _ { i } ( v )$ can be computed in polynomial time on the number of crossings [[#References|[a20]]]. |
| − | 6) If | + | 6) If $P _ { L } ( v , z ) = \sum _ { i = e } ^ { E } a _ { i } ( z ) v ^ { i }$ (with $\alpha _ { e} ( z ) \neq 0$, $a _ { E } ( z ) \neq 0$), then |
| − | + | \begin{equation*} ( n _ { + } - n _ { - } ) - ( s ( D _ { L } ) - 1 ) \leq e \leq E \leq ( n _ { + } - n _ { - } ) + ( s ( D _ { L } ) - 1 ), \end{equation*} | |
| − | where | + | where $n _ { + }$ (respectively, $n_-$) is the number of positive (respectively, negative) crossings of the diagram $D_{ L}$. In particular, $s ( L ) \geq ( E - e ) / 2$, where $s ( L )$ is the minimal number of Seifert circles of all diagrams $D_{ L}$ representing $L$; it is equal to the braid index of $L$, see [[#References|[a24]]]. The knot $9_{42}$ is the first knot for which the inequality is sharp. The smallest (known) alternating knot for which the inequality is sharp has $18$ crossings [[#References|[a16]]]. |
| − | 7) If | + | 7) If $P _ { L } ( v , z ) = \sum a _ { i ,j} v ^ { i } z ^ { j }$, then |
| − | + | \begin{equation*} a_{ ( n _ { + } - n _ { - } - s ( D _ { L } ) + 1 ) , ( n - s ( D _ { L } ) + 1 ) } \neq 0 \end{equation*} | |
| − | if and only if | + | if and only if $D_{ L}$ is a positive diagram (i.e. $n_{- } = 0$). For example, for a positive diagram of the right-handed trefoil knot with $3$ crossings one has $s ( D _ { 3_{1} } ) = 2$ and $a _ { 2 , 2} = 1$. |
| − | 8) For a knot | + | 8) For a knot $K$, $P _ { K } ( v , z ) - 1$ is a multiple of $( v ^ { - 1 } - v ) ^ { 2 } - z ^ { 2 }$. |
| − | For example, | + | For example, $P _ { 4 _ { 1 } } ( v , z ) - 1 = ( v ^ { - 1 } - v ) ^ { 2 } - z ^ { 2 } = - v ^ { - 2 } ( P _ { 3_1 } ( v , z ) - 1 ) = - v ^ { 2 } ( P _ { \overline{3}_1 } ( v , z ) - 1 )$. Setting |
| − | + | \begin{equation*} \mathsf{P} _ { K } ( v , z ) = \frac { P _ { K } ( v , z ) - 1 } { ( v ^ { - 1 } - v ) ^ { 2 } - z ^ { 2 } }, \end{equation*} | |
then | then | ||
| − | + | \begin{equation*} \mathsf{P} _ { K _ { + } } ( v , z ) - \mathsf{P} _ { K _ { - } } ( v , z ) \equiv \operatorname { lk } ( K _ { 0 } ) \operatorname { mod } ( v ^ { 2 } - 1 , z ), \end{equation*} | |
| − | where | + | where $\operatorname { lk } ( K _ { 0 } )$ is the linking number of $K _ { 0 }$. In particular, $\mathsf{P} _ { K } ( 1,0 ) = a _ { 2 }$ (the second coefficient of the [[Alexander–Conway polynomial|Alexander–Conway polynomial]] and the first non-trivial Vassiliev–Gusarov invariant). More generally, consider $P _ { L } ( v , z )$ as an element of the ring $R$ that is the subring of $\mathbf{Z} [ v ^ { \pm 1 } , z ^ { \pm 1 } ]$ generated by $v \pm 1$, $z$ and $( v ^ { - 1 } - v ) / z$. Then $P _ { L } ( v , z ) - P _ { T _ { \text{com} ( L ) }} ( v , z )$ is a multiple of $z ( ( ( v ^ { - 1 } - v ) / z ) ^ { 2 } - 1 )$. Furthermore, |
| − | + | \begin{equation*} \frac { P _ { L } ( v , z ) - P _ { T_{\operatorname{ com } ( L )}} ( v , z ) } { z \left( \left( \frac { v ^ { - 1 } - v } { z } \right) ^ { 2 } - 1 \right) } \equiv \end{equation*} | |
| − | + | \begin{equation*} \equiv - \operatorname { lk } ( L ) v \left( \frac { v ^ { - 1 } - v } { z } \right) ^ { \operatorname { com } ( L ) - 2 } \operatorname { mod } ( z ) \end{equation*} | |
| − | in | + | in $R$, where $\operatorname { lk } ( L )$ is the linking number of $L$. In particular, |
| − | + | \begin{equation*} \frac { P _ { 2_1 } ( v , z ) - \frac { v ^ { - 1 } - v } { z } } { z \left( \left( \frac { v ^ { - 1 } - v } { z } \right) ^ { 2 } - 1 \right) } = - v. \end{equation*} | |
The number of components of a link and its linking number can be recovered from the Jones–Conway polynomial. | The number of components of a link and its linking number can be recovered from the Jones–Conway polynomial. | ||
| − | 9) If | + | 9) If $P _ { K } ( v , z ) = v ^ { 2 c } \sum c _ { i, j } ( v ^ { 2 } - 1 ) ^ { i } z ^ { j }$ for a knot $K$ and some constant $c$, then $c_{i , j}$ is a Vassiliev–Gusarov invariant of order $i + j$. Equivalently, $P _ { K } ( v , z ) \operatorname { mod } ( ( ( v ^ { 2 } - 1 ) , z ) ^ { k + 1 } )$ is a Vassiliev–Gusarov invariant of order $k$. One can obtain a coloured Jones–Conway polynomial by choosing an element of the Jones–Conway [[Skein module|skein module]] of the solid torus (a linear combination of links in a solid torus) and computing for this the Jones–Conway polynomial. Such an invariant is stratified by Vassiliev–Gusarov invariants. |
| − | Computing the whole Jones–Conway polynomial is | + | Computing the whole Jones–Conway polynomial is $\cal N P$-hard [[#References|[a6]]] (so up to the conjecture that $\mathcal{N P} \neq \mathcal{P}$, the polynomial cannot be computed in polynomial time). Furthermore, computing most of the substitutions to the Jones–Conway polynomial is $\cal N P$-hard (even $\# \mathcal{P}$-hard). The exceptions have well understood interpretations [[#References|[a5]]]: |
| − | i) | + | i) $v = \pm 1$. Now $P _ { L }$ reduces to the [[Alexander–Conway polynomial|Alexander–Conway polynomial]]. |
| − | ii) | + | ii) $z = \pm ( v ^ { - 1 } - v )$. Compare 8) above. |
| − | iii) | + | iii) $( v , z ) = ( \pm i , \pm i \sqrt { 2 } )$, where the $\pm$'s are independent. For example, $P ( i , i \sqrt { 2 } ) = ( - \sqrt { 2 } ) ^ { \operatorname { com } ( L ) - 1 } ( - 1 ) ^ { \operatorname { Arf } ( L ) }$ if the [[Arf-invariant|Arf-invariant]] is defined and $0$ otherwise. |
| − | iv) | + | iv) $( v , z ) = ( \pm i , \pm i )$. E.g., $P _ { L } ( i , i ) = ( i \sqrt { 2 } ) ^ { \operatorname { dim } ( H _ { 1 } ( M ^ { ( 3 ) } , \mathbf{Z} _ { 2 } ) ) }$, where $M ^ { ( k ) }$ denotes the $k$-fold cyclic covering of $S ^ { 3 }$ branched over $L$. |
| − | v) | + | v) $( v , z ) = ( \pm e ^ { \pm \pi i / 3 } , \pm i )$. E.g., $P _ { L } ( e ^ { \pi i / 3 } , i ) = \varepsilon ( L ) i ^ { \operatorname { com } ( L ) - 1 } ( i \sqrt { 3 } ) ^ { \operatorname { dim } ( H _ { 1 } ( M ^ { ( 2 ) } , \mathbf{Z} _ { 3 } ) ) }$, where $\varepsilon ( L ) = \pm 1$ can be derived from the modulo $3$ linking form in $M ^ { ( 2 ) }$. |
There are several constructions of different links with the same Jones–Conway polynomial: mutation, rotation, cabling, spectral parameter tangle, etc. [[#References|[a22]]]. T. Kanenobu [[#References|[a12]]] has constructed an infinite family of different links with the same Jones–Conway polynomial. It is an open problem (as of 2001) whether there exists a non-trivial link with Jones–Conway polynomial equal to that of a trivial link (cf. [[Jones unknotting conjecture|Jones unknotting conjecture]]). | There are several constructions of different links with the same Jones–Conway polynomial: mutation, rotation, cabling, spectral parameter tangle, etc. [[#References|[a22]]]. T. Kanenobu [[#References|[a12]]] has constructed an infinite family of different links with the same Jones–Conway polynomial. It is an open problem (as of 2001) whether there exists a non-trivial link with Jones–Conway polynomial equal to that of a trivial link (cf. [[Jones unknotting conjecture|Jones unknotting conjecture]]). | ||
====References==== | ====References==== | ||
| − | <table>< | + | <table><tr><td valign="top">[a1]</td> <td valign="top"> P.R. Cromwell, "Homogeneous links" ''J. London Math. Soc.'' , '''39''' : 2 (1989) pp. 535–552</td></tr><tr><td valign="top">[a2]</td> <td valign="top"> J. Franks, R.F. Williams, "Braids and the Jones polynomial" ''Trans. Amer. Math. Soc.'' , '''303''' (1987) pp. 97–108</td></tr><tr><td valign="top">[a3]</td> <td valign="top"> J. Hoste, "A polynomial invariant of knots and links" ''Pacific J. Math.'' , '''124''' (1986) pp. 295–320</td></tr><tr><td valign="top">[a4]</td> <td valign="top"> P. Freyd, D. Yetter, J. Hoste, W.B.R. Lickorish, K. Millett, A. Ocneanu, "A new polynomial invariant of knots and links" ''Bull. Amer. Math. Soc.'' , '''12''' (1985) pp. 239–249</td></tr><tr><td valign="top">[a5]</td> <td valign="top"> F. Jaeger, D.L. Vertigan, D.J.A. Welsh, "On the computational complexity of the Jones and Tutte polynomials" ''Math. Proc. Cambridge Philos. Soc.'' , '''108''' (1990) pp. 35–53</td></tr><tr><td valign="top">[a6]</td> <td valign="top"> F. Jaeger, "On Tutte polynomials and link polynomials" ''Proc. Amer. Math. Soc.'' , '''103''' : 2 (1988) pp. 647–654</td></tr><tr><td valign="top">[a7]</td> <td valign="top"> F. Jaeger, "Composition products and models for the Homfly polynomial" ''L'Enseign. Math.'' , '''35''' (1989) pp. 323–361</td></tr><tr><td valign="top">[a8]</td> <td valign="top"> V.F.R. Jones, "Hecke algebra representations of braid groups and link polynomials" ''Ann. of Math.'' , '''126''' : 2 (1987) pp. 335–388</td></tr><tr><td valign="top">[a9]</td> <td valign="top"> V.F.R. Jones, "On knot invariants related to some statistical mechanical models" ''Pacific J. Math.'' , '''137''' : 2 (1989) pp. 311–334</td></tr><tr><td valign="top">[a10]</td> <td valign="top"> K. Kobayashi, K. Kodama, "On the $\operatorname { deg } _ { z } P _ { L } ( v , z )$ for plumbing diagrams and oriented arborescent links" ''Kobe J. Math.'' , '''5''' (1988) pp. 221–232</td></tr><tr><td valign="top">[a11]</td> <td valign="top"> J. Kania–Bartoszyńska, J.H. Przytycki, "Knots and links, revisited" ''Delta, Warsaw'' , '''June''' (1985) pp. 10–12 (In Polish)</td></tr><tr><td valign="top">[a12]</td> <td valign="top"> T. Kanenobu, "Infinitely many knots with the same polynomial invariant" ''Proc. Amer. Math. Soc.'' , '''97''' : 1 (1986) pp. 158–162</td></tr><tr><td valign="top">[a13]</td> <td valign="top"> W.B.R. Lickorish, "An introduction to knot theory" , Springer (1997)</td></tr><tr><td valign="top">[a14]</td> <td valign="top"> W.B.R. Lickorish, K. Millett, "A polynomial invariant of oriented links" ''Topology'' , '''26''' (1987) pp. 107–141</td></tr><tr><td valign="top">[a15]</td> <td valign="top"> K. Murasugi, J.H. Przytycki, "The Skein polynomial of a planar star product of two links" ''Math. Proc. Cambridge Philos. Soc.'' , '''106''' (1989) pp. 273–276</td></tr><tr><td valign="top">[a16]</td> <td valign="top"> K. Murasugi, J.H. Przytycki, "An index of a graph with applications to knot theory" , ''Memoirs'' , '''106''' , Amer. Math. Soc. (1993)</td></tr><tr><td valign="top">[a17]</td> <td valign="top"> H.R. Morton, H.B. Short, "The $2$-variable polynomial of cable knots" ''Math. Proc. Cambridge Philos. Soc.'' , '''101''' (1987) pp. 267–278</td></tr><tr><td valign="top">[a18]</td> <td valign="top"> H.R. Morton, "Seifert circles and knot polynomials" ''Math. Proc. Cambridge Philos. Soc.'' , '''99''' (1986) pp. 107–109</td></tr><tr><td valign="top">[a19]</td> <td valign="top"> H. Murakami, "On derivatives of the Jones polynomial" ''Kobe J. Math.'' , '''3''' (1986) pp. 61–64</td></tr><tr><td valign="top">[a20]</td> <td valign="top"> T.M. Przytycka, J.H. Przytycki, "Subexponentially computable truncations of Jones-type polynomials" , ''Graph Structure Theory'' , ''Contemp. Math.'' , '''147''' (1993) pp. 63–108</td></tr><tr><td valign="top">[a21]</td> <td valign="top"> J.H. Przytycki, P. Traczyk, "Invariants of links of Conway type" ''Kobe J. Math.'' , '''4''' (1987) pp. 115–139</td></tr><tr><td valign="top">[a22]</td> <td valign="top"> J.H. Przytycki, "Search for different links with the same Jones' type polynomials" , ''Ideas from Graph Theory and Statistical Mechanics, Panoramas of Mathematics'' , '''34''' , Banach Center Publ. (1995) pp. 121–148</td></tr><tr><td valign="top">[a23]</td> <td valign="top"> V.G. Turaev, "The Yang–Baxter equation and invariants of links" ''Invent. Math.'' , '''92''' (1988) pp. 527–553</td></tr><tr><td valign="top">[a24]</td> <td valign="top"> S. Yamada, "The minimal number of Seifert circles equals to braid index of a link" ''Invent. Math.'' , '''89''' (1987) pp. 347–356</td></tr></table> |
Revision as of 16:58, 1 July 2020
Homfly polynomial, Homflypt polynomial, skein polynomial
An invariant of oriented links.
It is a Laurent polynomial of two variables associated to ambient isotopy classes of oriented links in $\mathbf{R} ^ { 3 }$ (or $S ^ { 3 }$), constructed in 1984 by several groups of researchers (thus the acronyms Homfly and Homflypt) [a4], [a3], [a14], [a21], and denoted by $P _ { L } ( \square )$. It generalizes the Alexander–Conway polynomial and the Jones polynomial.
There are several constructions of the polynomial, using diagrams of links (and Reidemeister moves, cf. also Reidemeister theorem), the braid group (and the Alexander and Markov theorems, cf. also Braid theory; Alexander theorem on braids; Markov braid theorem), or statistical mechanics (interpreting the polynomial as a state sum, cf. also Statistical mechanics, mathematical problems in).
The first approach uses the recursive (skein) relation
\begin{equation*} v ^ { - 1 } P _ { L _ { + } } ( v , z ) - v P _ { L_- } ( v , z ) = z P _ { L _ { 0 } } ( v , z ), \end{equation*}
where $L _ { + }$, $L_{-}$ and $L_0$ form a Conway skein triple. The Jones–Conway polynomial is usually normalized to be $1$ for the trivial knot. Then for the trivial link of $n$ components, $T _ { n }$, one gets
\begin{equation*} P _ { T _ { n } } ( v , z ) = \left( \frac { v ^ { - 1 } - v } { z } \right) ^ { n - 1 }. \end{equation*}
Setting $v = t$ and $z = \sqrt { t } - 1 / \sqrt { t }$ yields the Jones polynomial, $V _ { L } ( t )$, and substituting $v = 1$ and $z = \sqrt { t } - 1 / \sqrt { t }$ yields the Alexander–Conway polynomial.
In the second approach one considers the Hecke algebra associated to the Artin braid group and constructs on it the Jones–Ocneanu trace, which essentially is invariant under Markov moves. This approach is strongly related to the first approach, as the Hecke algebra quadratic relation is analogous to the skein relation of the first method.
The third approach uses the fact that the statistical mechanical systems considered satisfy the Yang–Baxter equation. This approach is immediately related to the first two by the fact that a Yang–Baxter operator satisfies the minimal polynomial (leading to a skein relation) and, on the other hand, yields a linear representation of the braid group. This state sum approach was first developed by V.F.R. Jones and has a very nice reflection in the Jaeger composition product [a7].
Properties of the Jones–Conway polynomial.
1) $P _ { L } ( v , z )$ is an element of the Laurent polynomial ring $\mathbf{Z} [ v ^ { \pm 1 } , z ^ { \pm 1 } ]$. Furthermore, $( v z ) ^ { \operatorname { com } ( L ) - 1 } P _ { L } ( v , z ) \in \mathbf{Z} [ v ^ { \pm 2 } , z ^ { 2 } ]$, where $\operatorname { com}( L )$ denotes the number of components of $L$. In particular,
\begin{equation*} P _ { L } ( v , z ) = P _ { L } ( - v , - z ) = ( - 1 ) ^ { \operatorname { com } ( L ) - 1 } P _ { L } ( - v , z ). \end{equation*}
For example, for the right-handed Hopf link, $2_{1}$, one has
\begin{equation*} P _ { 2 _ { 1 } } = \frac { v - v ^ { 3 } } { z } + v z. \end{equation*}
2) If $\bar{L}$ denotes the mirror image of a link $L$, then
\begin{equation*} P _ { \overline{L} } ( v , z ) = P _ { L } ( - v ^ { - 1 } , z ). \end{equation*}
This property often allows one to detect lack of amphicheirality of a link. For example, for the right-handed trefoil knot, $3_1$, one has $P _ { 3_1 } = 2 v ^ { 2 } - v ^ { 4 } + v ^ { 2 } z ^ { 2 }$, so the trefoil knot is not amphicheiral. For the figure eight knot, $4_1$, which is amphicheiral, one gets $P _ { 4 _ { 1 } } = v ^ { - 2 } - 1 + v ^ { 2 } - z ^ { 2 }$. The first non-amphicheiral knot not detected by the Jones–Conway polynomial is the $9_{42}$ knot. The Kauffman polynomial also does not detect non-amphicheirality of $9_{42}$. However, one can use the Jones–Conway polynomial of the $2$-cable of $9_{42}$ to see that it is non-amphicheiral.
3) Next,
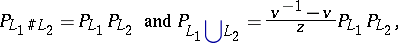 |
where $\#$ denotes the connected sum and $\cup$ the split sum of links. Because the connected sum of links may depend on the choice of connected components, one can use the connected sum formula to find different links with the same Jones–Conway polynomial, for example the connected sum of three Hopf links can give two different results, both with the polynomial equal to $( ( v - v ^ { 3 } ) / z + v z ) ^ { 3 }$.
4) If $L^-$ denotes the link obtained by reversing the orientation of $L$, then the Jones–Conway polynomials of $L$ and $L^-$ coincide. Thus, each non-reversible knot ($8 _ { 17 }$ is the smallest example) gives rise to an example of different knots with the same Jones–Conway polynomial. Furthermore, if $K _ { 1 }$ and $K _ { 2 }$ are two non-reversible knots, then $K _ { 1 } \# K _ { 2 }$ and $K _ { 1 } \# K _ { 2 } ^ { - }$ are different knots which cannot be distinguished by the Jones–Conway polynomials (nor by the Kauffman polynomials) of their satellites. It is an open problem (as of 2001) whether they can be distinguished by any Vassiliev–Gusarov invariants.
If $P _ { L } ( v , z ) = \sum _ { i = m } ^ { M } P _ { i } ( v ) z ^ { i }$ (with $P _ { m } ( v ) \neq 0$, $P _ { M } ( v ) \neq 0$), then $m = 1 - \operatorname { com } ( L )$ and $M \leq \operatorname { cr } ( D _ { L } ) - s ( D _ { L } ) + 1$, where $D_{ L}$ is any diagram of $L$, $\operatorname { cr } ( D _ { L } )$ denotes the number of crossings of $D_{ L}$ and $s ( D _ { L } )$ is the number of Seifert circles of $D_{ L}$. The equality holds, e.g., for homogeneous diagrams (including positive and alternating diagrams). In particular for a non-trivial knot $K$, $M < \text{cr} ( K )$ where $\operatorname { cr } ( K )$ is the crossing number of $K$, i.e. the minimum over all diagrams of $L$ of the crossing number.
5) If $\varphi ( D ) = \operatorname { cr } ( D _ { L } ) - s ( D _ { L } ) + 1$, then
\begin{equation*} P _ { \varphi ( D _ { 1 } * D _ { 2 } )} ( v ) = P _ { \varphi ( D _ { 1 } )} ( v ) P _ { \varphi ( D _ { 2 } )} ( v ), \end{equation*}
where $D _ { 1 } * D _ { 2 }$ denotes the planar star (Murasugi) product of the diagrams $D _ { 1 }$ and $D _ { 2 }$ [a15]. D.L. Vertigan proved that for a fixed $i$, $P _ { i } ( v )$ can be computed in polynomial time on the number of crossings [a20].
6) If $P _ { L } ( v , z ) = \sum _ { i = e } ^ { E } a _ { i } ( z ) v ^ { i }$ (with $\alpha _ { e} ( z ) \neq 0$, $a _ { E } ( z ) \neq 0$), then
\begin{equation*} ( n _ { + } - n _ { - } ) - ( s ( D _ { L } ) - 1 ) \leq e \leq E \leq ( n _ { + } - n _ { - } ) + ( s ( D _ { L } ) - 1 ), \end{equation*}
where $n _ { + }$ (respectively, $n_-$) is the number of positive (respectively, negative) crossings of the diagram $D_{ L}$. In particular, $s ( L ) \geq ( E - e ) / 2$, where $s ( L )$ is the minimal number of Seifert circles of all diagrams $D_{ L}$ representing $L$; it is equal to the braid index of $L$, see [a24]. The knot $9_{42}$ is the first knot for which the inequality is sharp. The smallest (known) alternating knot for which the inequality is sharp has $18$ crossings [a16].
7) If $P _ { L } ( v , z ) = \sum a _ { i ,j} v ^ { i } z ^ { j }$, then
\begin{equation*} a_{ ( n _ { + } - n _ { - } - s ( D _ { L } ) + 1 ) , ( n - s ( D _ { L } ) + 1 ) } \neq 0 \end{equation*}
if and only if $D_{ L}$ is a positive diagram (i.e. $n_{- } = 0$). For example, for a positive diagram of the right-handed trefoil knot with $3$ crossings one has $s ( D _ { 3_{1} } ) = 2$ and $a _ { 2 , 2} = 1$.
8) For a knot $K$, $P _ { K } ( v , z ) - 1$ is a multiple of $( v ^ { - 1 } - v ) ^ { 2 } - z ^ { 2 }$.
For example, $P _ { 4 _ { 1 } } ( v , z ) - 1 = ( v ^ { - 1 } - v ) ^ { 2 } - z ^ { 2 } = - v ^ { - 2 } ( P _ { 3_1 } ( v , z ) - 1 ) = - v ^ { 2 } ( P _ { \overline{3}_1 } ( v , z ) - 1 )$. Setting
\begin{equation*} \mathsf{P} _ { K } ( v , z ) = \frac { P _ { K } ( v , z ) - 1 } { ( v ^ { - 1 } - v ) ^ { 2 } - z ^ { 2 } }, \end{equation*}
then
\begin{equation*} \mathsf{P} _ { K _ { + } } ( v , z ) - \mathsf{P} _ { K _ { - } } ( v , z ) \equiv \operatorname { lk } ( K _ { 0 } ) \operatorname { mod } ( v ^ { 2 } - 1 , z ), \end{equation*}
where $\operatorname { lk } ( K _ { 0 } )$ is the linking number of $K _ { 0 }$. In particular, $\mathsf{P} _ { K } ( 1,0 ) = a _ { 2 }$ (the second coefficient of the Alexander–Conway polynomial and the first non-trivial Vassiliev–Gusarov invariant). More generally, consider $P _ { L } ( v , z )$ as an element of the ring $R$ that is the subring of $\mathbf{Z} [ v ^ { \pm 1 } , z ^ { \pm 1 } ]$ generated by $v \pm 1$, $z$ and $( v ^ { - 1 } - v ) / z$. Then $P _ { L } ( v , z ) - P _ { T _ { \text{com} ( L ) }} ( v , z )$ is a multiple of $z ( ( ( v ^ { - 1 } - v ) / z ) ^ { 2 } - 1 )$. Furthermore,
\begin{equation*} \frac { P _ { L } ( v , z ) - P _ { T_{\operatorname{ com } ( L )}} ( v , z ) } { z \left( \left( \frac { v ^ { - 1 } - v } { z } \right) ^ { 2 } - 1 \right) } \equiv \end{equation*}
\begin{equation*} \equiv - \operatorname { lk } ( L ) v \left( \frac { v ^ { - 1 } - v } { z } \right) ^ { \operatorname { com } ( L ) - 2 } \operatorname { mod } ( z ) \end{equation*}
in $R$, where $\operatorname { lk } ( L )$ is the linking number of $L$. In particular,
\begin{equation*} \frac { P _ { 2_1 } ( v , z ) - \frac { v ^ { - 1 } - v } { z } } { z \left( \left( \frac { v ^ { - 1 } - v } { z } \right) ^ { 2 } - 1 \right) } = - v. \end{equation*}
The number of components of a link and its linking number can be recovered from the Jones–Conway polynomial.
9) If $P _ { K } ( v , z ) = v ^ { 2 c } \sum c _ { i, j } ( v ^ { 2 } - 1 ) ^ { i } z ^ { j }$ for a knot $K$ and some constant $c$, then $c_{i , j}$ is a Vassiliev–Gusarov invariant of order $i + j$. Equivalently, $P _ { K } ( v , z ) \operatorname { mod } ( ( ( v ^ { 2 } - 1 ) , z ) ^ { k + 1 } )$ is a Vassiliev–Gusarov invariant of order $k$. One can obtain a coloured Jones–Conway polynomial by choosing an element of the Jones–Conway skein module of the solid torus (a linear combination of links in a solid torus) and computing for this the Jones–Conway polynomial. Such an invariant is stratified by Vassiliev–Gusarov invariants.
Computing the whole Jones–Conway polynomial is $\cal N P$-hard [a6] (so up to the conjecture that $\mathcal{N P} \neq \mathcal{P}$, the polynomial cannot be computed in polynomial time). Furthermore, computing most of the substitutions to the Jones–Conway polynomial is $\cal N P$-hard (even $\# \mathcal{P}$-hard). The exceptions have well understood interpretations [a5]:
i) $v = \pm 1$. Now $P _ { L }$ reduces to the Alexander–Conway polynomial.
ii) $z = \pm ( v ^ { - 1 } - v )$. Compare 8) above.
iii) $( v , z ) = ( \pm i , \pm i \sqrt { 2 } )$, where the $\pm$'s are independent. For example, $P ( i , i \sqrt { 2 } ) = ( - \sqrt { 2 } ) ^ { \operatorname { com } ( L ) - 1 } ( - 1 ) ^ { \operatorname { Arf } ( L ) }$ if the Arf-invariant is defined and $0$ otherwise.
iv) $( v , z ) = ( \pm i , \pm i )$. E.g., $P _ { L } ( i , i ) = ( i \sqrt { 2 } ) ^ { \operatorname { dim } ( H _ { 1 } ( M ^ { ( 3 ) } , \mathbf{Z} _ { 2 } ) ) }$, where $M ^ { ( k ) }$ denotes the $k$-fold cyclic covering of $S ^ { 3 }$ branched over $L$.
v) $( v , z ) = ( \pm e ^ { \pm \pi i / 3 } , \pm i )$. E.g., $P _ { L } ( e ^ { \pi i / 3 } , i ) = \varepsilon ( L ) i ^ { \operatorname { com } ( L ) - 1 } ( i \sqrt { 3 } ) ^ { \operatorname { dim } ( H _ { 1 } ( M ^ { ( 2 ) } , \mathbf{Z} _ { 3 } ) ) }$, where $\varepsilon ( L ) = \pm 1$ can be derived from the modulo $3$ linking form in $M ^ { ( 2 ) }$.
There are several constructions of different links with the same Jones–Conway polynomial: mutation, rotation, cabling, spectral parameter tangle, etc. [a22]. T. Kanenobu [a12] has constructed an infinite family of different links with the same Jones–Conway polynomial. It is an open problem (as of 2001) whether there exists a non-trivial link with Jones–Conway polynomial equal to that of a trivial link (cf. Jones unknotting conjecture).
References
| [a1] | P.R. Cromwell, "Homogeneous links" J. London Math. Soc. , 39 : 2 (1989) pp. 535–552 |
| [a2] | J. Franks, R.F. Williams, "Braids and the Jones polynomial" Trans. Amer. Math. Soc. , 303 (1987) pp. 97–108 |
| [a3] | J. Hoste, "A polynomial invariant of knots and links" Pacific J. Math. , 124 (1986) pp. 295–320 |
| [a4] | P. Freyd, D. Yetter, J. Hoste, W.B.R. Lickorish, K. Millett, A. Ocneanu, "A new polynomial invariant of knots and links" Bull. Amer. Math. Soc. , 12 (1985) pp. 239–249 |
| [a5] | F. Jaeger, D.L. Vertigan, D.J.A. Welsh, "On the computational complexity of the Jones and Tutte polynomials" Math. Proc. Cambridge Philos. Soc. , 108 (1990) pp. 35–53 |
| [a6] | F. Jaeger, "On Tutte polynomials and link polynomials" Proc. Amer. Math. Soc. , 103 : 2 (1988) pp. 647–654 |
| [a7] | F. Jaeger, "Composition products and models for the Homfly polynomial" L'Enseign. Math. , 35 (1989) pp. 323–361 |
| [a8] | V.F.R. Jones, "Hecke algebra representations of braid groups and link polynomials" Ann. of Math. , 126 : 2 (1987) pp. 335–388 |
| [a9] | V.F.R. Jones, "On knot invariants related to some statistical mechanical models" Pacific J. Math. , 137 : 2 (1989) pp. 311–334 |
| [a10] | K. Kobayashi, K. Kodama, "On the $\operatorname { deg } _ { z } P _ { L } ( v , z )$ for plumbing diagrams and oriented arborescent links" Kobe J. Math. , 5 (1988) pp. 221–232 |
| [a11] | J. Kania–Bartoszyńska, J.H. Przytycki, "Knots and links, revisited" Delta, Warsaw , June (1985) pp. 10–12 (In Polish) |
| [a12] | T. Kanenobu, "Infinitely many knots with the same polynomial invariant" Proc. Amer. Math. Soc. , 97 : 1 (1986) pp. 158–162 |
| [a13] | W.B.R. Lickorish, "An introduction to knot theory" , Springer (1997) |
| [a14] | W.B.R. Lickorish, K. Millett, "A polynomial invariant of oriented links" Topology , 26 (1987) pp. 107–141 |
| [a15] | K. Murasugi, J.H. Przytycki, "The Skein polynomial of a planar star product of two links" Math. Proc. Cambridge Philos. Soc. , 106 (1989) pp. 273–276 |
| [a16] | K. Murasugi, J.H. Przytycki, "An index of a graph with applications to knot theory" , Memoirs , 106 , Amer. Math. Soc. (1993) |
| [a17] | H.R. Morton, H.B. Short, "The $2$-variable polynomial of cable knots" Math. Proc. Cambridge Philos. Soc. , 101 (1987) pp. 267–278 |
| [a18] | H.R. Morton, "Seifert circles and knot polynomials" Math. Proc. Cambridge Philos. Soc. , 99 (1986) pp. 107–109 |
| [a19] | H. Murakami, "On derivatives of the Jones polynomial" Kobe J. Math. , 3 (1986) pp. 61–64 |
| [a20] | T.M. Przytycka, J.H. Przytycki, "Subexponentially computable truncations of Jones-type polynomials" , Graph Structure Theory , Contemp. Math. , 147 (1993) pp. 63–108 |
| [a21] | J.H. Przytycki, P. Traczyk, "Invariants of links of Conway type" Kobe J. Math. , 4 (1987) pp. 115–139 |
| [a22] | J.H. Przytycki, "Search for different links with the same Jones' type polynomials" , Ideas from Graph Theory and Statistical Mechanics, Panoramas of Mathematics , 34 , Banach Center Publ. (1995) pp. 121–148 |
| [a23] | V.G. Turaev, "The Yang–Baxter equation and invariants of links" Invent. Math. , 92 (1988) pp. 527–553 |
| [a24] | S. Yamada, "The minimal number of Seifert circles equals to braid index of a link" Invent. Math. , 89 (1987) pp. 347–356 |
Jones-Conway polynomial. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Jones-Conway_polynomial&oldid=50281