Markov braid theorem
From Encyclopedia of Mathematics
If two closed braids represent the same ambient isotopy class of oriented links (cf. also Braid theory), then one can transform one braid to another by a sequence of Markov moves:
i) $a \leftrightarrow b a b ^ { - 1 }$ (conjugation).
ii) $a \leftrightarrow a b ^ { \pm 1 }_ { n }$, where $a$ is an element of the $n$th braid group
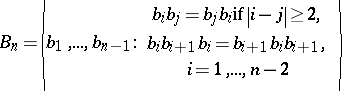 |
and $b _ { n }$ is the $n$th generator of the $( n + 1 )$th braid group.
Markov's braid theorem is an important ingredient in the construction of the Jones polynomial and its generalizations (e.g. the Jones–Conway polynomial).
References
| [a1] | J.S. Birman, "Braids, links and mapping class groups", Ann. of Math. Stud., 82 , Princeton Univ. Press (1974) |
| [a2] | A.A. Markov, "Über die freie Äquivalenz der geschlossenen Zöpfe", Recueil Math. Moscou, 1 (1935) pp. 73–78 Zbl 0014.04202 |
| [a3] | N.M. Weinberg, "On free equivalence of free braids", C.R. (Dokl.) Acad. Sci. USSR, 23 (1939) pp. 215–216 (In Russian) |
How to Cite This Entry:
Markov braid theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_braid_theorem&oldid=52948
Markov braid theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Markov_braid_theorem&oldid=52948
This article was adapted from an original article by Jozef Przytycki (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article