Yang-Baxter equation
Let $ R $
be an $ ( n ^ {2} \times n ^ {2} ) $-
matrix with entries $ r _ {kl} ^ {ij} $.
View $ R $
as an endomorphism of $ \mathbf C ^ {n} \otimes \mathbf C ^ {n} $
with basis $ e _ {i} \otimes e _ {j} $(
$ i, j = 1 \dots n $),
so that
$$ \tag{a1 } R( e _ {i} \otimes e _ {j} ) = \sum _ {a ,b } r _ {ij} ^ {ab} e _ {a} \otimes e _ {b} . $$
The constant Yang–Baxter equation, or quantum Yang–Baxter equation, for $ R $ is:
$$ \tag{a2 } R ^ {12} R ^ {13} R ^ {23} = R ^ {23} R ^ {13} R ^ {12} , $$
where $ R ^ {ij} $ is the endomorphism of $ \mathbf C ^ {n} \otimes \mathbf C ^ {n} \otimes \mathbf C ^ {n} $ acting like $ R $ on the two factors $ i, j $ and leaving the third factor alone. Thus, $ R ^ {12} = R \otimes \mathop{\rm id} $, $ R ^ {23} = \mathop{\rm id} \otimes R $ and
$$ \tag{a3 } R ^ {13} ( e _ {i} \otimes e _ {j} \otimes e _ {k} ) = \ \sum _ {a, b } r _ {ik} ^ {ab} e _ {a} \otimes e _ {j} \otimes e _ {b} . $$
An alternative form of the Yang–Baxter equation is:
$$ \tag{a4 } \widetilde{R} {} ^ {12} \widetilde{R} {} ^ {23} \widetilde{R} {} ^ {12} = \ \widetilde{R} {} ^ {23} \widetilde{R} {} ^ {12} \widetilde{R} {} ^ {23} . $$
$ R $ is a solution of (a2) if and only if $ \widetilde{R} = PR $ is a solution of (a4), where $ P $ is the $ ( n ^ {2} \times n ^ {2} ) $- matrix $ P = ( p _ {kl} ^ {ij} ) $, $ p _ {kl} ^ {ij} = \delta _ {il} \delta _ {jk} $, which switches the two factors of $ \mathbf C ^ {n} \otimes \mathbf C ^ {n} $.
The Yang–Baxter equation (a2) can be interpreted as a condition on the interaction of relativistic particles with internal state space $ \mathbf C ^ {n} $, [a2]. Let the interaction between two particles with rapidities $ \lambda , \mu $ be given by $ R ( \lambda , \mu ) : \mathbf C ^ {n} \otimes \mathbf C ^ {n} \rightarrow \mathbf C ^ {n} \otimes \mathbf C ^ {n} $; then the Yang–Baxter equation
$$ \tag{a5 } R ^ {12} ( \lambda , \mu ) R ^ {13} ( \lambda , \nu ) R ^ {23} ( \mu , \nu ) = $$
$$ = \ R ^ {23} ( \mu , \nu ) R ^ {13} ( \lambda , \nu ) R ^ {12} ( \lambda , \mu ) $$
expresses the condition that the interaction between three particles is determined by the two particle interactions and is independent of which particles interact first. In this connection the Yang–Baxter equation is also called the factorization equation. It occurred first in [a5], [a6]. In lattice statistical mechanics there is another interpretation of the Yang–Baxter equation, [a3], [a4]. In this context it is also called the triangle equation or the star-triangle equation. Its sources go back to [a7].
If $ \widetilde{R} $ satisfies (a4), let $ \widetilde{R} {} _ {i} = \mathop{\rm id} \otimes \dots \otimes \mathop{\rm id} \otimes \widetilde{R} \otimes \mathop{\rm id} \otimes \dots \otimes \mathop{\rm id} $, where there are $ i- 1 $ factors $ \mathop{\rm id} $ before $ \widetilde{R} $ and $ n - i - 1 $ factors $ \mathop{\rm id} $ after $ \widetilde{R} $. Then $ \sigma _ {i} \mapsto \widetilde{R} {} _ {i} $ defines a representation of the braid group $ B _ {n} $, where $ \sigma _ {i} $ is the $ i $- th simple braid, cf. Braid theory. This is one main reason for the interconnection between knot and braid theory on the one hand and quantum field theory and statistical mechanics on the other, cf. e.g. [a9].
A generalization of the Yang–Baxter equation are the fundamental commutation relations
$$ \tag{a6 } R ( \lambda , \mu ) ( T ( \lambda ) \otimes T( \mu )) = \ ( T ( \mu ) \otimes T ( \lambda )) R( \lambda , \mu ) , $$
introduced by L.D. Faddeev, E.K. Sklyanin, L.A. Takhtazhyan as a basis for their quantum inverse scattering method, [a8]. In (a6), $ R ( \lambda , \mu ) $ is an $ ( n ^ {2} \times n ^ {2} ) $- matrix of scalars (as before; usually satisfying the Yang–Baxter equation) and $ T ( \lambda ) $ is an $ ( n \times n ) $- matrix of operators. Equation (a6) serves as a starting point for using an (algebraic) Bethe Ansatz for calculating eigenvalues and eigenvectors of the Hamiltonian operator $ t( \lambda ) = \mathop{\rm Tr} ( T ( \lambda )) $. Solutions of (a6) relate to families of representations of certain Hopf algebras, in particular (duals of) quasi-triangular Hopf algebras, cf. Quantum groups and [a14], [a15], [a11].
The classical Yang–Baxter equation is the semi-classical limit of (a2). It is
$$ \tag{a7 } [ X ^ {12} ( u _ {1} , u _ {2} ) , X ^ {13} ( u _ {1} , u _ {3} ) ] + $$
$$ + [ X ^ {12} ( u _ {1} , u _ {2} ), X ^ {23} ( u _ {2} , u _ {3} ) ]+ [ X ^ {13} ( u _ {1} , u _ {3} ) , X ^ {23} ( u _ {2} , u _ {3} )] = 0 , $$
where $ X( u , v) $ is a function with values in $ \mathfrak g \otimes \mathfrak g $, where $ \mathfrak g $ is a Lie algebra. (To interpret (a7), imbed $ \mathfrak g $ in its universal enveloping algebra $ U \mathfrak g $: the meaning of $ X ^ {12} $, etc. is analogous to the case of equation (a2).) The classical Yang–Baxter equation has much to do with completely-integrable Hamiltonian systems (cf. Hamiltonian system; Soliton), cf. [a12], and the results of [a13] go some way to explaining why solutions to soliton equations typically involve principally elliptic, trigonometric and rational functions.
References
| [a1] | M. Jimbo (ed.) , Yang–Baxter equation in integrable systems , World Sci. (1990) |
| [a2] | A.B. Zamolodchikov, Al.B. Zamolodchikov, "Factorized 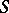 -matrices in two dimensions as the exact solutions of certain relativistic quantum field theory models" Ann. Physics , 120 (1979) pp. 253–291 ((Reprinted in [A1], 82–120.)) -matrices in two dimensions as the exact solutions of certain relativistic quantum field theory models" Ann. Physics , 120 (1979) pp. 253–291 ((Reprinted in [A1], 82–120.)) |
| [a3] | R.J. Baxter, "Solvable eight-vertex model on an arbitrary planar lattice" Phil. Trans. Royal Soc. London , 289 (1978) pp. 315–346 ((Reprinted in [A1], 50–81.)) |
| [a4] | R.J. Baxter, "Exactly solved models in statistical mechanics" , Acad. Press (1982) |
| [a5] | J.B. McGuire, "Study of exactly solvable one-dimensional 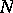 -body problems" J. Math. Physics , 5 (1964) pp. 622–636 -body problems" J. Math. Physics , 5 (1964) pp. 622–636 |
| [a6] | C.N. Yang, "Some exact results for the many-body problem in one dimension with delta-function interaction" Phys. Rev. Lett. , 19 (1967) pp. 1312–1314 |
| [a7] | L. Onsager, "Crystal lattices I. A two dimensional model with an order-disorder transition" Phys. Rev. , 65 (1944) pp. 117–149 |
| [a8] | L.D. Faddeev, "Integrable models in (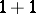 )-dimensional quantum field theory" , Lectures in Les Houches, 1982 , Session 39 , Elsevier (1982) pp. 563–608 )-dimensional quantum field theory" , Lectures in Les Houches, 1982 , Session 39 , Elsevier (1982) pp. 563–608 |
| [a9] | C.N. Yang (ed.) M.L. Ge (ed.) , Braid group, knot theory and statistical mechanics , World Sci. (1989) |
| [a10] | M. Jimbo, "Introduction to the Yang–Baxter equation" M. Jimbo (ed.) , Yang–Baxter equation in integrable systems , World Sci. (1990) pp. 111–134 |
| [a11] | M. Hazewinkel, "Introductory recommendations for the study of Hopf algebras in mathematics and physics" CWI Quarterly , 4 (1991) pp. 3–26 |
| [a12] | M.A. Semenov-Tyan-Shanskii, "What is a classical  -matrix" Funct. Anal. Appl. , 17 (1984) pp. 259–272 ((Reprinted in [A1], 226–2242.)) Funkts. Anal. Prilozh. , 17 : 4 (1983) pp. 17–33 -matrix" Funct. Anal. Appl. , 17 (1984) pp. 259–272 ((Reprinted in [A1], 226–2242.)) Funkts. Anal. Prilozh. , 17 : 4 (1983) pp. 17–33 |
| [a13] | A.A. Belavin, V.G. Drinfel'd, "Solutions of the classical Yang–Baxter equation for simple Lie algebras" Funct. Anal. Appl. , 16 (1983) pp. 159–180 ((Reprinted in [A1], 200–221.)) Funkts. Anal. Prilozh. , 16 : 3 (1982) pp. 1–29 |
| [a14] | V.V. Lyubashenko, "Hopf algebras and vector symmetries" Russ. Math. Surveys , 41 (1986) pp. 153–154 Uspekhi Mat. Nauk , 41 (1986) pp. 185–186 |
| [a15] | L.D. Faddeev, N.Yu. Reshetikhin, L.A. Takhtadzhyan, "Quantization of Lie groups and Lie algebras" Algebra and Analysis , 1 (1989) pp. 178–206 (In Russian) |
Yang–Baxter equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Yang%E2%80%93Baxter_equation&oldid=23156