Difference between revisions of "Abelian surface"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | a1100401.png | ||
| + | $#A+1 = 261 n = 12 | ||
| + | $#C+1 = 261 : ~/encyclopedia/old_files/data/A110/A.1100040 Abelian surface | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | An [[Abelian variety|Abelian variety]] of dimension two, i.e. a complete connected group variety of dimension two over a field $ k $. | |
| + | The group law is commutative. In the sequel, $ k $ | ||
| + | is assumed to be algebraically closed (cf. [[Algebraically closed field|Algebraically closed field]]). | ||
| − | + | In the classification of algebraic surfaces, Abelian surfaces are exactly the smooth complete surfaces $ A $ | |
| + | with [[Kodaira dimension|Kodaira dimension]] $ \kappa = 0 $, | ||
| + | [[Geometric genus|geometric genus]] $ p _ {g} = h ^ {2} ( A, {\mathcal O} _ {A} ) =1 $ | ||
| + | and [[Irregularity|irregularity]] $ q = h ^ {1} ( A, {\mathcal O} _ {A} ) = 2 $. | ||
| − | + | For an Abelian surface $ A $, | |
| + | the dual Abelian variety $ {\widehat{A} } = { \mathop{\rm Pic} } ^ {0} ( A ) $ | ||
| + | is again an Abelian surface. An invertible [[Sheaf|sheaf]] $ L $ | ||
| + | on $ A $ | ||
| + | defines the homomorphism $ {\phi _ {L} } : A \rightarrow { {\widehat{A} } } $, | ||
| + | $ a \mapsto t _ {a} ^ {*} L \otimes L ^ {- 1 } $. | ||
| + | The homomorphism $ \phi _ {L} $ | ||
| + | depends only on the algebraic equivalence class of $ L $. | ||
| + | The invertible sheaf $ L $ | ||
| + | is ample (cf. [[Ample sheaf|Ample sheaf]]) if and only if $ \phi _ {L} $ | ||
| + | is an [[Isogeny|isogeny]] (i.e., $ \phi _ {L} $ | ||
| + | is surjective and has finite kernel) and $ h ^ {0} ( A,L ) \neq0 $. | ||
| + | In this case, $ { \mathop{\rm deg} } \phi _ {L} = d ^ {2} $ | ||
| + | with a positive integer $ d $ | ||
| + | and the [[Riemann–Roch theorem|Riemann–Roch theorem]] says that | ||
| − | + | $$ | |
| + | h ^ {0} ( A,L ) = { | ||
| + | \frac{1}{2} | ||
| + | } ( L ^ {2} ) = d, | ||
| + | $$ | ||
| − | + | where $ ( L ^ {2} ) $ | |
| + | denotes the self-intersection number. Every Abelian surface admits an ample invertible sheaf and hence is projective (cf. [[Projective scheme|Projective scheme]]). | ||
| − | A polarization | + | A polarization $ \lambda $ |
| + | on $ A $ | ||
| + | is the algebraic equivalence class $ [ L ] $ | ||
| + | of an ample invertible sheaf $ L $. | ||
| + | The degree $ { \mathop{\rm deg} } \lambda $ | ||
| + | of $ \lambda $ | ||
| + | is by definition $ d = \sqrt { { \mathop{\rm deg} } \phi _ {L} } $. | ||
| + | An Abelian surface $ A $ | ||
| + | together with a polarization $ \lambda $ | ||
| + | is a polarized Abelian surface. A principal polarization is a polarization of degree $ 1 $. | ||
| + | A principally polarized Abelian surface $ ( A, \lambda ) $ | ||
| + | is either the [[Jacobi variety|Jacobi variety]] $ J ( H ) $ | ||
| + | of a smooth projective curve $ H $ | ||
| + | of genus $ 2 $, | ||
| + | and $ \lambda = \theta $ | ||
| + | is the class of the theta divisor, or $ A $ | ||
| + | is the product of two elliptic curves (Abelian varieties of dimension one, cf. also [[Elliptic curve|Elliptic curve]]) with $ \lambda $ | ||
| + | the product polarization. | ||
| − | + | If the degree of $ \lambda = [ L ] $ | |
| + | is prime to $ { \mathop{\rm char} } ( k ) $, | ||
| + | then $ \lambda $ | ||
| + | is said to be a separable polarization and the kernel of $ \phi _ {L} $ | ||
| + | is isomorphic to the group $ ( \mathbf Z/d _ {1} \mathbf Z ) ^ {2} \times ( \mathbf Z/d _ {2} \mathbf Z ) ^ {2} $, | ||
| + | where $ d _ {1} $ | ||
| + | and $ d _ {2} $ | ||
| + | are positive integers such that $ d _ {1} $ | ||
| + | divides $ d _ {2} $ | ||
| + | and $ d _ {1} d _ {2} = { \mathop{\rm deg} } \lambda $. | ||
| + | The pair $ ( d _ {1} ,d _ {2} ) $ | ||
| + | is the type of the polarized Abelian surface $ ( A, \lambda ) $. | ||
| − | + | A polarization $ \lambda = [ L ] $ | |
| + | of type $ ( d _ {1} ,d _ {2} ) $ | ||
| + | on $ A $ | ||
| + | defines a polarization $ {\widehat \lambda } = [ {\widehat{L} } ] $ | ||
| + | on the dual Abelian surface $ {\widehat{A} } $. | ||
| + | The polarization $ {\widehat \lambda } $ | ||
| + | is again of type $ ( d _ {1} ,d _ {2} ) $ | ||
| + | and it is characterized by each of the following two equivalent properties: | ||
| − | + | $$ | |
| + | \phi _ {L} ^ {*} {\widehat \lambda } = d _ {1} d _ {2} \lambda \iff \phi _ { {\widehat{L} } } \phi _ {L} = d _ {1} d _ {2} { \mathop{\rm id} } _ {A} . | ||
| + | $$ | ||
| − | + | For a polarized Abelian surface $ ( A, \lambda = [ L ] ) $ | |
| + | of type $ ( d _ {1} ,d _ {2} ) $, | ||
| + | the assignment $ A \ni a \mapsto \{ {\sigma \in H ^ {0} ( A,L ) } : {\sigma ( a ) = 0 } \} \subset H ^ {0} ( A,L ) $ | ||
| + | defines a rational mapping from $ A $ | ||
| + | into the projective space of hyperplanes in $ H ^ {0} ( A,L ) $: | ||
| + | |||
| + | $$ | ||
| + | {\varphi _ {L} } : A \rightarrow {\mathbf P ( H ^ {0} ( A,L ) ^ {*} ) } \simeq \mathbf P _ {k} ^ {d _ {1} d _ {2} - 1 } . | ||
| + | $$ | ||
| + | |||
| + | If $ d _ {1} \geq 2 $, | ||
| + | then $ \varphi _ {L} $ | ||
| + | is everywhere defined. The Lefschetz theorem says that for $ d _ {1} \geq 3 $ | ||
| + | the morphism $ \varphi _ {L} $ | ||
| + | is an embedding. Suppose $ d _ {1} = 2 $; | ||
| + | then $ \lambda = 2 \mu $ | ||
| + | with a polarization $ \mu = [ M ] $ | ||
| + | of type $ ( 1, { {d _ {2} } / 2 } ) $. | ||
| + | If the linear system $ | M | $ | ||
| + | has no fixed components, then $ \varphi _ {L} $ | ||
| + | is an embedding. | ||
==Complex Abelian surfaces.== | ==Complex Abelian surfaces.== | ||
| − | An Abelian surface over the field | + | An Abelian surface over the field $ \mathbf C $ |
| + | of complex numbers is a [[Complex torus|complex torus]] | ||
| − | + | $$ | |
| + | A = { {\mathbf C ^ {2} } / \Lambda } | ||
| + | $$ | ||
| − | (with a lattice | + | (with a lattice $ \Lambda \simeq \mathbf Z ^ {4} $ |
| + | in $ \mathbf C ^ {2} $) | ||
| + | admitting a polarization. A polarization $ \lambda $ | ||
| + | on $ A $ | ||
| + | can be considered as a non-degenerate alternating form $ \Lambda \times \Lambda \rightarrow \mathbf Z $, | ||
| + | the elementary divisors of which are given by the type $ ( d _ {1} ,d _ {2} ) $ | ||
| + | of $ \lambda $. | ||
| − | In the sequel, the field | + | In the sequel, the field $ k $ |
| + | is assumed to be $ \mathbf C $, | ||
| + | although some of the following results are also valid for arbitrary algebraically closed fields. | ||
| − | Suppose | + | Suppose $ ( A, \lambda = [ L ] ) $ |
| + | is of type $ ( 1,d ) $ | ||
| + | and the linear system $ | L | $ | ||
| + | has no fixed components. The Reider theorem states that for $ d \geq 5 $ | ||
| + | the invertible sheaf $ L $ | ||
| + | is very ample if and only if there is no elliptic curve $ E $ | ||
| + | on $ A $ | ||
| + | with $ ( E \cdot L ) = 2 $( | ||
| + | see [[#References|[a14]]] and [[#References|[a10]]]). For arbitrary $ d \geq 1 $ | ||
| + | there exist finitely many isogenies $ f : {( A, \lambda ) } \rightarrow {( B, \theta ) } $ | ||
| + | of degree $ d $ | ||
| + | onto principally polarized Abelian surfaces (cf. also [[Isogeny|Isogeny]]). Suppose $ \theta = [ \Theta ] $ | ||
| + | with a symmetric invertible sheaf $ \Theta $( | ||
| + | i.e., $ ( -1 ) _ {A} ^ {*} \Theta \simeq \Theta $) | ||
| + | and let $ H $ | ||
| + | be the unique divisor in the linear system $ | \Theta | $. | ||
| + | The divisor $ C = f ^ {- 1 } ( H ) $ | ||
| + | on $ A $ | ||
| + | defines a symmetric invertible sheaf $ L = {\mathcal O} _ {A} ( C ) $ | ||
| + | with class $ [ L ] = \lambda $ | ||
| + | and the covering $ {f \mid _ {C} } : C \rightarrow H $ | ||
| + | is étale of degree $ d $. | ||
| + | One distinguishes two cases: i) $ H $ | ||
| + | is smooth of genus $ 2 $, | ||
| + | $ B = J ( H ) $ | ||
| + | and $ C $ | ||
| + | is smooth of genus $ d + 1 $; | ||
| + | and ii) $ H $ | ||
| + | is the sum $ E _ {1} + E _ {2} $ | ||
| + | of two elliptic curves with intersection number $ ( E _ {1} \cdot E _ {2} ) = 1 $, | ||
| + | $ B = E _ {1} \times E _ {2} $ | ||
| + | and $ C $ | ||
| + | is the sum $ F _ {1} + F _ {2} $ | ||
| + | of two elliptic curves with $ ( F _ {1} \cdot F _ {2} ) = d $. | ||
| − | In the following list, | + | In the following list, $ ( A, \lambda = [ L ] ) $ |
| + | is a polarized Abelian surface of type $ ( d _ {1} ,d _ {2} ) $ | ||
| + | such that $ | L | $ | ||
| + | admits no fixed components | ||
| − | Type | + | Type $ ( 1,2 ) $— |
| + | The linear system $ | L | $ | ||
| + | has exactly $ 4 $ | ||
| + | base points. The blow-up $ {\widetilde{A} } $ | ||
| + | of $ A $ | ||
| + | in these points admits a morphism $ { {\widetilde \varphi } _ {L} } : { {\widetilde{A} } } \rightarrow {\mathbf P ^ {1} } $ | ||
| + | induced by $ \varphi _ {L} $. | ||
| + | The general fibre of $ {\widetilde \varphi } _ {L} $ | ||
| + | is a smooth curve of genus $ 3 $. | ||
| + | The curve $ C $ | ||
| + | on $ A $ | ||
| + | defining $ L $ | ||
| + | as above is double elliptic: $ C { \mathop \rightarrow \limits ^ { {2:1 }} } E $ | ||
| + | with an elliptic curve $ E $, | ||
| + | and $ A $ | ||
| + | is isomorphic to $ { {J ( C ) } / E } $( | ||
| + | see [[#References|[a3]]]). | ||
| − | Type | + | Type $ ( 1,3 ) $— |
| + | $ L $ | ||
| + | defines a $ 6 $- | ||
| + | fold covering $ {\varphi _ {L} } : A \rightarrow {\mathbf P ^ {2} } $ | ||
| + | ramified along a curve $ R \subset \mathbf P ^ {2} $ | ||
| + | of degree $ 18 $. | ||
| + | The general divisor in the linear system $ | L | $ | ||
| + | is a smooth curve of genus $ 4 $. | ||
| + | There are $ 4 $ | ||
| + | isogenies $ f : {( A, \lambda ) } \rightarrow {( B, \theta ) } $ | ||
| + | of degree $ 3 $ | ||
| + | onto principally polarized Abelian surfaces. In case i) the smooth genus- $ 4 $ | ||
| + | curve $ C \in | L | $ | ||
| + | is double elliptic: $ C { \mathop \rightarrow \limits ^ { {2:1 }} } E $, | ||
| + | and the embedding of $ E $ | ||
| + | into the Jacobian $ J ( C ) $ | ||
| + | induces an exact sequence | ||
| − | + | $$ | |
| + | 0 \rightarrow E \times E \rightarrow J ( C ) \rightarrow A \rightarrow 0. | ||
| + | $$ | ||
| − | The étale | + | The étale $ 3 $- |
| + | fold covering $ {f \mid _ {C} } : C \rightarrow H $ | ||
| + | induces a morphism $ {f ^ {*} } : {J ( H ) } \rightarrow {J ( C ) } $ | ||
| + | with image $ {\widehat{A} } $, | ||
| + | the dual Abelian surface of $ A $( | ||
| + | see [[#References|[a7]]]). | ||
| − | Type | + | Type $ ( 1,4 ) $— |
| + | There are $ 24 $ | ||
| + | isogenies $ f : {( A, \lambda ) } \rightarrow {( B, \theta ) } $ | ||
| + | of degree $ 4 $ | ||
| + | onto principally polarized Abelian surfaces. If the curves $ C $ | ||
| + | and $ H $ | ||
| + | do not admit elliptic involutions compatible with $ f $, | ||
| + | then $ \varphi _ {L} :A \atR {\overline{A}\; } \subset \mathbf P ^ {3} $ | ||
| + | is a birational morphism onto a singular octic $ {\overline{A}\; } $. | ||
| + | In the exceptional case, $ \varphi _ {L} : A \atR {\overline{A}\; } \subset \mathbf P ^ {3} $ | ||
| + | is a double covering of a singular quartic $ {\overline{A}\; } $, | ||
| + | which is birational to an elliptic scroll. In the first case the octic $ {\overline{A}\; } $ | ||
| + | is smooth outside the four coordinate planes of $ \mathbf P ^ {3} $ | ||
| + | and touches the coordinate planes in curves $ D _ {i} $, | ||
| + | $ i = 1 \dots 4 $, | ||
| + | of degree $ 4 $. | ||
| + | Each of the curves $ D _ {i} $ | ||
| + | has $ 3 $ | ||
| + | double points and passes through $ 12 $ | ||
| + | pinch points of $ {\overline{A}\; } $. | ||
| + | The octic is a $ 8:1 $ | ||
| + | covering of a [[Kummer surface|Kummer surface]]: $ p: {\overline{A}\; } \atR K \subset \mathbf P ^ {3} $( | ||
| + | see also Type $ ( 2,2 ) $ | ||
| + | below). The restrictions $ p \mid _ {D _ {i} } $ | ||
| + | are $ 4 $- | ||
| + | fold coverings of four double conics of $ K $ | ||
| + | lying on a coordinate tetrahedron. The three double points of $ D _ {i} $ | ||
| + | map to three double points of $ K $ | ||
| + | on the conic $ p ( D _ {i} ) $ | ||
| + | and the $ 12 $ | ||
| + | pinch points on $ D _ {i} $ | ||
| + | map to the other three double points on the double conic $ p ( D _ {i} ) $( | ||
| + | see [[#References|[a6]]]). | ||
| − | Type | + | Type $ ( 1,5 ) $— |
| + | The invertible sheaf $ L $ | ||
| + | is very ample, i.e. $ {\varphi _ {L} } : A \rightarrow {\mathbf P ^ {4} } $ | ||
| + | is an embedding if and only if the curves $ C $ | ||
| + | and $ H $ | ||
| + | do not admit elliptic involutions compatible with $ f $. | ||
| + | In the exceptional case $ \varphi _ {L} $ | ||
| + | is a double covering of an elliptic scroll (see [[#References|[a13]]] and [[#References|[a9]]]). If $ L $ | ||
| + | is very ample, $ \varphi _ {L} ( A ) $ | ||
| + | is a smooth surface of degree $ 10 $ | ||
| + | in $ \mathbf P ^ {4} $. | ||
| + | It is the zero locus of a section of the Horrocks–Mumford bundle $ F $( | ||
| + | see [[#References|[a8]]]). Conversely, the zero set $ \{ \sigma = 0 \} \subset \mathbf P ^ {4} $ | ||
| + | of a general section $ \sigma \in H ^ {0} ( \mathbf P ^ {4} ,F ) $ | ||
| + | is an Abelian surface of degree $ 10 $, | ||
| + | i.e. of type $ ( 1,5 ) $. | ||
| − | Type | + | Type $ ( 2,2 ) $— |
| + | $ \lambda $ | ||
| + | is twice a principal polarization on $ A $. | ||
| + | The morphism $ \varphi _ {L} : A \atR K _ {A} \subset \mathbf P ^ {3} $ | ||
| + | is a double covering of the [[Kummer surface|Kummer surface]] $ K _ {A} $ | ||
| + | associated with $ A $. | ||
| + | It is isomorphic to $ {A / {( - 1 ) _ {A} } } $. | ||
| − | Type | + | Type $ ( 2,4 ) $— |
| + | The ideal sheaf $ {\mathcal I} _ { {A / {\mathbf P ^ {7} } } } $ | ||
| + | of the image of the embedding $ \varphi _ {L} : A \ahR \mathbf P ^ {7} $ | ||
| + | is generated by $ 6 $ | ||
| + | quadrics (see [[#References|[a3]]]). | ||
| − | Type | + | Type $ ( 2,6 ) $— |
| + | Suppose $ L $ | ||
| + | is very ample and let $ K _ {A} = {A / {( - 1 ) _ {A} } } $ | ||
| + | be the associated Kummer surface. The subvector space $ H ^ {0} ( A,L ) ^ {-} \subset H ^ {0} ( A,L ) $ | ||
| + | of odd sections induces an embedding of $ {\widetilde{K} } _ {A} $, | ||
| + | the blow-up of $ K _ {A} $ | ||
| + | in the $ 16 $ | ||
| + | double points, as a smooth quartic surface into $ \mathbf P ^ {3} $. | ||
| + | $ {\widetilde{K} } _ {A} \subset \mathbf P ^ {3} $ | ||
| + | is invariant under the action of the level- $ 2 $ | ||
| + | Heisenberg group (cf. also [[Heisenberg representation|Heisenberg representation]]) $ H ( 2,2 ) $. | ||
| + | The $ 16 $ | ||
| + | blown-up double points become skew lines on the quartic surface. Any $ H ( 2,2 ) $- | ||
| + | invariant quartic surface in $ \mathbf P ^ {3} $ | ||
| + | with $ 16 $ | ||
| + | skew lines comes from a polarized Abelian surface $ ( A, \lambda ) $ | ||
| + | of type $ ( 2,6 ) $ | ||
| + | in this way (see [[#References|[a5]]], [[#References|[a11]]] and [[#References|[a12]]]). | ||
| − | Type | + | Type $ ( 3,3 ) $— |
| + | $ \lambda $ | ||
| + | is three times a principal polarization and $ \varphi _ {L} : A \ahR \mathbf P ^ {8} $ | ||
| + | is an embedding. If $ ( A, \lambda ) $ | ||
| + | is not a product, then the quadrics $ Q \in H ^ {0} ( \mathbf P ^ {8} , {\mathcal I} _ { {A / {\mathbf P ^ {8} } } } ( 2 ) ) $ | ||
| + | vanishing on $ A $ | ||
| + | generate the ideal sheaf $ {\mathcal I} _ { {A / {\mathbf P ^ {8} } } } $. | ||
| + | In the product case, $ {\mathcal I} _ { {A / {\mathbf P ^ {8} } } } $ | ||
| + | is generated by quadrics and cubics (see [[#References|[a4]]]). | ||
==Algebraic completely integrable systems.== | ==Algebraic completely integrable systems.== | ||
| − | An algebraic completely integrable system in the sense of M. Adler and P. van Moerbeke is a completely integrable polynomial [[Hamiltonian system|Hamiltonian system]] on | + | An algebraic completely integrable system in the sense of M. Adler and P. van Moerbeke is a completely integrable polynomial [[Hamiltonian system|Hamiltonian system]] on $ \mathbf C ^ {N} $( |
| + | with Casimir functions $ {H _ {1} \dots H _ {k} } : {\mathbf C ^ {N} } \rightarrow \mathbf C $ | ||
| + | and $ m = { {( N - k ) } / 2 } $ | ||
| + | independent constants of motion $ H _ {k + 1 } \dots H _ {k + m } $ | ||
| + | in involution) such that: | ||
| − | a) for a general point | + | a) for a general point $ c = {} ^ {t} ( c _ {1} \dots c _ {k + m } ) \in \mathbf C ^ {k + m } $ |
| + | the invariant manifold $ A _ {c} ^ {o} = \cap _ {i = 1 } ^ {m + k } \{ H _ {i} = c _ {i} \} \subset \mathbf C ^ {N} $ | ||
| + | is an open affine part of an Abelian variety $ A _ {c} $; | ||
| − | b) the flows of the integrable vector fields | + | b) the flows of the integrable vector fields $ X _ {u _ {i} } $ |
| + | linearize on the Abelian varieties $ A _ {c} $[[#References|[a2]]]. | ||
| − | The divisor at infinity | + | The divisor at infinity $ D _ {c} = A _ {c} - A _ {c} ^ {o} $ |
| + | defines a polarization on $ A _ {c} $. | ||
| + | In this way the mapping $ {( H _ {1} \dots H _ {k + m } ) } : {\mathbf C ^ {N} } \rightarrow {\mathbf C ^ {k + m } } $ | ||
| + | defines a family of polarized Abelian varieties (cf. [[Moduli problem|Moduli problem]]). Some examples of $ 2 $- | ||
| + | dimensional algebraic completely integrable systems and their associated Abelian surfaces are: | ||
the three-body Toda lattice and the even, respectively odd, master systems (cf. also [[Master equations in cooperative and social phenomena|Master equations in cooperative and social phenomena]]) linearize on principally polarized Abelian surfaces; | the three-body Toda lattice and the even, respectively odd, master systems (cf. also [[Master equations in cooperative and social phenomena|Master equations in cooperative and social phenomena]]) linearize on principally polarized Abelian surfaces; | ||
| − | the [[Kowalewski top|Kowalewski top]], the Hénon–Heiles system and the Manakov geodesic flow on | + | the [[Kowalewski top|Kowalewski top]], the Hénon–Heiles system and the Manakov geodesic flow on $ { \mathop{\rm SO} } ( 4 ) $ |
| + | linearize on Abelian surfaces of type $ ( 1,2 ) $[[#References|[a1]]]; | ||
| − | the Garnier system linearizes on Abelian surfaces of type | + | the Garnier system linearizes on Abelian surfaces of type $ ( 1,4 ) $[[#References|[a15]]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Adler, P. van Moerbeke, "The Kowalewski and Hénon–Heiles motions as Manakov geodesic flows on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040262.png" />: a two-dimensional family of Lax pairs" ''Comm. Math. Phys.'' , '''113''' (1988) pp. 659–700</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Adler, P. van Moerbeke, "The complex geometry of the Kowalewski–Painlevé analysis" ''Invent. Math.'' , '''97''' (1989) pp. 3–51 {{MR|}} {{ZBL|0678.58020}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Barth, "Abelian surfaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040263.png" />-polarization" , ''Algebraic Geometry, Sendai, 1985'' , ''Advanced Studies in Pure Math.'' , '''10''' (1987) pp. 41–84 {{MR|946234}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W. Barth, "Quadratic equations for level-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040264.png" /> abelian surfaces" , ''Abelian Varieties, Proc. Workshop Egloffstein 1993'' , de Gruyter (1995) pp. 1–18 {{MR|1336597}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Barth, I. Nieto, "Abelian surfaces of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040265.png" /> and quartic surfaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040266.png" /> skew lines" ''J. Algebraic Geom.'' , '''3''' (1994) pp. 173–222 {{MR|1257320}} {{ZBL|0809.14027}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Ch. Birkenhake, H. Lange, D. van Straten, "Abelian surfaces of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040267.png" />" ''Math. Ann.'' , '''285''' (1989) pp. 625–646 {{MR|1027763}} {{ZBL|0714.14028}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> Ch. Birkenhake, H. Lange, "Moduli spaces of Abelian surfaces wih isogeny" , ''Geometry and Analysis, Bombay Colloquium 1992'' , Tata Inst. Fundam. Res. (1995) pp. 225–243 {{MR|1351509}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> G. Horrocks, D. Mumford, "A rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040268.png" /> vector bundle on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040269.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040270.png" /> symmetries" ''Topology'' , '''12''' (1973) pp. 63–81 {{MR|382279}} {{ZBL|0255.14017}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> K. Hulek, H. Lange, "Examples of abelian surfaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040271.png" />" ''J. Reine Angew. Math.'' , '''363''' (1985) pp. 200–216 {{MR|0814021}} {{ZBL|0593.14027}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> H. Lange, Ch. Birkenhake, "Complex Abelian varieties" , ''Grundlehren math. Wiss.'' , '''302''' , Springer (1992) {{MR|1217487}} {{ZBL|0779.14012}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Naruki, "On smooth quartic embeddings of Kummer surfaces" ''Proc. Japan Acad.'' , '''67 A''' (1991) pp. 223–224 {{MR|1137912}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> V. V. Nikulin, "On Kummer surfaces" ''Math USSR Izv.'' , '''9''' (1975) pp. 261–275 (In Russian) {{MR|429917}} {{ZBL|0325.14015}} </TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> S. Ramanan, "Ample divisors on abelian surfaces" ''Proc. London Math. Soc.'' , '''51''' (1985) pp. 231–245 {{MR|0794112}} {{ZBL|0603.14013}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> I. Reider, "Vector bundles of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040272.png" /> and linear systems on algebraic surfaces" ''Ann. of Math.'' , '''127''' (1988) pp. 309–316 {{MR|0932299}} {{ZBL|0663.14010}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> P. Vanhaecke, "A special case of the Garnier system, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040273.png" />-polarized Abelian surfaces and their moduli" ''Compositio Math.'' , '''92''' (1994) pp. 157–203 {{MR|1283227}} {{ZBL|}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Adler, P. van Moerbeke, "The Kowalewski and Hénon–Heiles motions as Manakov geodesic flows on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040262.png" />: a two-dimensional family of Lax pairs" ''Comm. Math. Phys.'' , '''113''' (1988) pp. 659–700</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> M. Adler, P. van Moerbeke, "The complex geometry of the Kowalewski–Painlevé analysis" ''Invent. Math.'' , '''97''' (1989) pp. 3–51 {{MR|}} {{ZBL|0678.58020}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> W. Barth, "Abelian surfaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040263.png" />-polarization" , ''Algebraic Geometry, Sendai, 1985'' , ''Advanced Studies in Pure Math.'' , '''10''' (1987) pp. 41–84 {{MR|946234}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> W. Barth, "Quadratic equations for level-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040264.png" /> abelian surfaces" , ''Abelian Varieties, Proc. Workshop Egloffstein 1993'' , de Gruyter (1995) pp. 1–18 {{MR|1336597}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> W. Barth, I. Nieto, "Abelian surfaces of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040265.png" /> and quartic surfaces with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040266.png" /> skew lines" ''J. Algebraic Geom.'' , '''3''' (1994) pp. 173–222 {{MR|1257320}} {{ZBL|0809.14027}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> Ch. Birkenhake, H. Lange, D. van Straten, "Abelian surfaces of type <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040267.png" />" ''Math. Ann.'' , '''285''' (1989) pp. 625–646 {{MR|1027763}} {{ZBL|0714.14028}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> Ch. Birkenhake, H. Lange, "Moduli spaces of Abelian surfaces wih isogeny" , ''Geometry and Analysis, Bombay Colloquium 1992'' , Tata Inst. Fundam. Res. (1995) pp. 225–243 {{MR|1351509}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a8]</TD> <TD valign="top"> G. Horrocks, D. Mumford, "A rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040268.png" /> vector bundle on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040269.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040270.png" /> symmetries" ''Topology'' , '''12''' (1973) pp. 63–81 {{MR|382279}} {{ZBL|0255.14017}} </TD></TR><TR><TD valign="top">[a9]</TD> <TD valign="top"> K. Hulek, H. Lange, "Examples of abelian surfaces in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040271.png" />" ''J. Reine Angew. Math.'' , '''363''' (1985) pp. 200–216 {{MR|0814021}} {{ZBL|0593.14027}} </TD></TR><TR><TD valign="top">[a10]</TD> <TD valign="top"> H. Lange, Ch. Birkenhake, "Complex Abelian varieties" , ''Grundlehren math. Wiss.'' , '''302''' , Springer (1992) {{MR|1217487}} {{ZBL|0779.14012}} </TD></TR><TR><TD valign="top">[a11]</TD> <TD valign="top"> I. Naruki, "On smooth quartic embeddings of Kummer surfaces" ''Proc. Japan Acad.'' , '''67 A''' (1991) pp. 223–224 {{MR|1137912}} {{ZBL|}} </TD></TR><TR><TD valign="top">[a12]</TD> <TD valign="top"> V. V. Nikulin, "On Kummer surfaces" ''Math USSR Izv.'' , '''9''' (1975) pp. 261–275 (In Russian) {{MR|429917}} {{ZBL|0325.14015}} </TD></TR><TR><TD valign="top">[a13]</TD> <TD valign="top"> S. Ramanan, "Ample divisors on abelian surfaces" ''Proc. London Math. Soc.'' , '''51''' (1985) pp. 231–245 {{MR|0794112}} {{ZBL|0603.14013}} </TD></TR><TR><TD valign="top">[a14]</TD> <TD valign="top"> I. Reider, "Vector bundles of rank <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040272.png" /> and linear systems on algebraic surfaces" ''Ann. of Math.'' , '''127''' (1988) pp. 309–316 {{MR|0932299}} {{ZBL|0663.14010}} </TD></TR><TR><TD valign="top">[a15]</TD> <TD valign="top"> P. Vanhaecke, "A special case of the Garnier system, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110040/a110040273.png" />-polarized Abelian surfaces and their moduli" ''Compositio Math.'' , '''92''' (1994) pp. 157–203 {{MR|1283227}} {{ZBL|}} </TD></TR></table> | ||
Revision as of 16:08, 1 April 2020
An Abelian variety of dimension two, i.e. a complete connected group variety of dimension two over a field $ k $.
The group law is commutative. In the sequel, $ k $
is assumed to be algebraically closed (cf. Algebraically closed field).
In the classification of algebraic surfaces, Abelian surfaces are exactly the smooth complete surfaces $ A $ with Kodaira dimension $ \kappa = 0 $, geometric genus $ p _ {g} = h ^ {2} ( A, {\mathcal O} _ {A} ) =1 $ and irregularity $ q = h ^ {1} ( A, {\mathcal O} _ {A} ) = 2 $.
For an Abelian surface $ A $, the dual Abelian variety $ {\widehat{A} } = { \mathop{\rm Pic} } ^ {0} ( A ) $ is again an Abelian surface. An invertible sheaf $ L $ on $ A $ defines the homomorphism $ {\phi _ {L} } : A \rightarrow { {\widehat{A} } } $, $ a \mapsto t _ {a} ^ {*} L \otimes L ^ {- 1 } $. The homomorphism $ \phi _ {L} $ depends only on the algebraic equivalence class of $ L $. The invertible sheaf $ L $ is ample (cf. Ample sheaf) if and only if $ \phi _ {L} $ is an isogeny (i.e., $ \phi _ {L} $ is surjective and has finite kernel) and $ h ^ {0} ( A,L ) \neq0 $. In this case, $ { \mathop{\rm deg} } \phi _ {L} = d ^ {2} $ with a positive integer $ d $ and the Riemann–Roch theorem says that
$$ h ^ {0} ( A,L ) = { \frac{1}{2} } ( L ^ {2} ) = d, $$
where $ ( L ^ {2} ) $ denotes the self-intersection number. Every Abelian surface admits an ample invertible sheaf and hence is projective (cf. Projective scheme).
A polarization $ \lambda $ on $ A $ is the algebraic equivalence class $ [ L ] $ of an ample invertible sheaf $ L $. The degree $ { \mathop{\rm deg} } \lambda $ of $ \lambda $ is by definition $ d = \sqrt { { \mathop{\rm deg} } \phi _ {L} } $. An Abelian surface $ A $ together with a polarization $ \lambda $ is a polarized Abelian surface. A principal polarization is a polarization of degree $ 1 $. A principally polarized Abelian surface $ ( A, \lambda ) $ is either the Jacobi variety $ J ( H ) $ of a smooth projective curve $ H $ of genus $ 2 $, and $ \lambda = \theta $ is the class of the theta divisor, or $ A $ is the product of two elliptic curves (Abelian varieties of dimension one, cf. also Elliptic curve) with $ \lambda $ the product polarization.
If the degree of $ \lambda = [ L ] $ is prime to $ { \mathop{\rm char} } ( k ) $, then $ \lambda $ is said to be a separable polarization and the kernel of $ \phi _ {L} $ is isomorphic to the group $ ( \mathbf Z/d _ {1} \mathbf Z ) ^ {2} \times ( \mathbf Z/d _ {2} \mathbf Z ) ^ {2} $, where $ d _ {1} $ and $ d _ {2} $ are positive integers such that $ d _ {1} $ divides $ d _ {2} $ and $ d _ {1} d _ {2} = { \mathop{\rm deg} } \lambda $. The pair $ ( d _ {1} ,d _ {2} ) $ is the type of the polarized Abelian surface $ ( A, \lambda ) $.
A polarization $ \lambda = [ L ] $ of type $ ( d _ {1} ,d _ {2} ) $ on $ A $ defines a polarization $ {\widehat \lambda } = [ {\widehat{L} } ] $ on the dual Abelian surface $ {\widehat{A} } $. The polarization $ {\widehat \lambda } $ is again of type $ ( d _ {1} ,d _ {2} ) $ and it is characterized by each of the following two equivalent properties:
$$ \phi _ {L} ^ {*} {\widehat \lambda } = d _ {1} d _ {2} \lambda \iff \phi _ { {\widehat{L} } } \phi _ {L} = d _ {1} d _ {2} { \mathop{\rm id} } _ {A} . $$
For a polarized Abelian surface $ ( A, \lambda = [ L ] ) $ of type $ ( d _ {1} ,d _ {2} ) $, the assignment $ A \ni a \mapsto \{ {\sigma \in H ^ {0} ( A,L ) } : {\sigma ( a ) = 0 } \} \subset H ^ {0} ( A,L ) $ defines a rational mapping from $ A $ into the projective space of hyperplanes in $ H ^ {0} ( A,L ) $:
$$ {\varphi _ {L} } : A \rightarrow {\mathbf P ( H ^ {0} ( A,L ) ^ {*} ) } \simeq \mathbf P _ {k} ^ {d _ {1} d _ {2} - 1 } . $$
If $ d _ {1} \geq 2 $, then $ \varphi _ {L} $ is everywhere defined. The Lefschetz theorem says that for $ d _ {1} \geq 3 $ the morphism $ \varphi _ {L} $ is an embedding. Suppose $ d _ {1} = 2 $; then $ \lambda = 2 \mu $ with a polarization $ \mu = [ M ] $ of type $ ( 1, { {d _ {2} } / 2 } ) $. If the linear system $ | M | $ has no fixed components, then $ \varphi _ {L} $ is an embedding.
Complex Abelian surfaces.
An Abelian surface over the field $ \mathbf C $ of complex numbers is a complex torus
$$ A = { {\mathbf C ^ {2} } / \Lambda } $$
(with a lattice $ \Lambda \simeq \mathbf Z ^ {4} $ in $ \mathbf C ^ {2} $) admitting a polarization. A polarization $ \lambda $ on $ A $ can be considered as a non-degenerate alternating form $ \Lambda \times \Lambda \rightarrow \mathbf Z $, the elementary divisors of which are given by the type $ ( d _ {1} ,d _ {2} ) $ of $ \lambda $.
In the sequel, the field $ k $ is assumed to be $ \mathbf C $, although some of the following results are also valid for arbitrary algebraically closed fields.
Suppose $ ( A, \lambda = [ L ] ) $ is of type $ ( 1,d ) $ and the linear system $ | L | $ has no fixed components. The Reider theorem states that for $ d \geq 5 $ the invertible sheaf $ L $ is very ample if and only if there is no elliptic curve $ E $ on $ A $ with $ ( E \cdot L ) = 2 $( see [a14] and [a10]). For arbitrary $ d \geq 1 $ there exist finitely many isogenies $ f : {( A, \lambda ) } \rightarrow {( B, \theta ) } $ of degree $ d $ onto principally polarized Abelian surfaces (cf. also Isogeny). Suppose $ \theta = [ \Theta ] $ with a symmetric invertible sheaf $ \Theta $( i.e., $ ( -1 ) _ {A} ^ {*} \Theta \simeq \Theta $) and let $ H $ be the unique divisor in the linear system $ | \Theta | $. The divisor $ C = f ^ {- 1 } ( H ) $ on $ A $ defines a symmetric invertible sheaf $ L = {\mathcal O} _ {A} ( C ) $ with class $ [ L ] = \lambda $ and the covering $ {f \mid _ {C} } : C \rightarrow H $ is étale of degree $ d $. One distinguishes two cases: i) $ H $ is smooth of genus $ 2 $, $ B = J ( H ) $ and $ C $ is smooth of genus $ d + 1 $; and ii) $ H $ is the sum $ E _ {1} + E _ {2} $ of two elliptic curves with intersection number $ ( E _ {1} \cdot E _ {2} ) = 1 $, $ B = E _ {1} \times E _ {2} $ and $ C $ is the sum $ F _ {1} + F _ {2} $ of two elliptic curves with $ ( F _ {1} \cdot F _ {2} ) = d $.
In the following list, $ ( A, \lambda = [ L ] ) $ is a polarized Abelian surface of type $ ( d _ {1} ,d _ {2} ) $ such that $ | L | $ admits no fixed components
Type $ ( 1,2 ) $— The linear system $ | L | $ has exactly $ 4 $ base points. The blow-up $ {\widetilde{A} } $ of $ A $ in these points admits a morphism $ { {\widetilde \varphi } _ {L} } : { {\widetilde{A} } } \rightarrow {\mathbf P ^ {1} } $ induced by $ \varphi _ {L} $. The general fibre of $ {\widetilde \varphi } _ {L} $ is a smooth curve of genus $ 3 $. The curve $ C $ on $ A $ defining $ L $ as above is double elliptic: $ C { \mathop \rightarrow \limits ^ { {2:1 }} } E $ with an elliptic curve $ E $, and $ A $ is isomorphic to $ { {J ( C ) } / E } $( see [a3]).
Type $ ( 1,3 ) $— $ L $ defines a $ 6 $- fold covering $ {\varphi _ {L} } : A \rightarrow {\mathbf P ^ {2} } $ ramified along a curve $ R \subset \mathbf P ^ {2} $ of degree $ 18 $. The general divisor in the linear system $ | L | $ is a smooth curve of genus $ 4 $. There are $ 4 $ isogenies $ f : {( A, \lambda ) } \rightarrow {( B, \theta ) } $ of degree $ 3 $ onto principally polarized Abelian surfaces. In case i) the smooth genus- $ 4 $ curve $ C \in | L | $ is double elliptic: $ C { \mathop \rightarrow \limits ^ { {2:1 }} } E $, and the embedding of $ E $ into the Jacobian $ J ( C ) $ induces an exact sequence
$$ 0 \rightarrow E \times E \rightarrow J ( C ) \rightarrow A \rightarrow 0. $$
The étale $ 3 $- fold covering $ {f \mid _ {C} } : C \rightarrow H $ induces a morphism $ {f ^ {*} } : {J ( H ) } \rightarrow {J ( C ) } $ with image $ {\widehat{A} } $, the dual Abelian surface of $ A $( see [a7]).
Type $ ( 1,4 ) $— There are $ 24 $ isogenies $ f : {( A, \lambda ) } \rightarrow {( B, \theta ) } $ of degree $ 4 $ onto principally polarized Abelian surfaces. If the curves $ C $ and $ H $ do not admit elliptic involutions compatible with $ f $, then $ \varphi _ {L} :A \atR {\overline{A}\; } \subset \mathbf P ^ {3} $ is a birational morphism onto a singular octic $ {\overline{A}\; } $. In the exceptional case, $ \varphi _ {L} : A \atR {\overline{A}\; } \subset \mathbf P ^ {3} $ is a double covering of a singular quartic $ {\overline{A}\; } $, which is birational to an elliptic scroll. In the first case the octic $ {\overline{A}\; } $ is smooth outside the four coordinate planes of $ \mathbf P ^ {3} $ and touches the coordinate planes in curves $ D _ {i} $, $ i = 1 \dots 4 $, of degree $ 4 $. Each of the curves $ D _ {i} $ has $ 3 $ double points and passes through $ 12 $ pinch points of $ {\overline{A}\; } $. The octic is a $ 8:1 $ covering of a Kummer surface: $ p: {\overline{A}\; } \atR K \subset \mathbf P ^ {3} $( see also Type $ ( 2,2 ) $ below). The restrictions $ p \mid _ {D _ {i} } $ are $ 4 $- fold coverings of four double conics of $ K $ lying on a coordinate tetrahedron. The three double points of $ D _ {i} $ map to three double points of $ K $ on the conic $ p ( D _ {i} ) $ and the $ 12 $ pinch points on $ D _ {i} $ map to the other three double points on the double conic $ p ( D _ {i} ) $( see [a6]).
Type $ ( 1,5 ) $— The invertible sheaf $ L $ is very ample, i.e. $ {\varphi _ {L} } : A \rightarrow {\mathbf P ^ {4} } $ is an embedding if and only if the curves $ C $ and $ H $ do not admit elliptic involutions compatible with $ f $. In the exceptional case $ \varphi _ {L} $ is a double covering of an elliptic scroll (see [a13] and [a9]). If $ L $ is very ample, $ \varphi _ {L} ( A ) $ is a smooth surface of degree $ 10 $ in $ \mathbf P ^ {4} $. It is the zero locus of a section of the Horrocks–Mumford bundle $ F $( see [a8]). Conversely, the zero set $ \{ \sigma = 0 \} \subset \mathbf P ^ {4} $ of a general section $ \sigma \in H ^ {0} ( \mathbf P ^ {4} ,F ) $ is an Abelian surface of degree $ 10 $, i.e. of type $ ( 1,5 ) $.
Type $ ( 2,2 ) $— $ \lambda $ is twice a principal polarization on $ A $. The morphism $ \varphi _ {L} : A \atR K _ {A} \subset \mathbf P ^ {3} $ is a double covering of the Kummer surface $ K _ {A} $ associated with $ A $. It is isomorphic to $ {A / {( - 1 ) _ {A} } } $.
Type $ ( 2,4 ) $— The ideal sheaf $ {\mathcal I} _ { {A / {\mathbf P ^ {7} } } } $ of the image of the embedding $ \varphi _ {L} : A \ahR \mathbf P ^ {7} $ is generated by $ 6 $ quadrics (see [a3]).
Type $ ( 2,6 ) $— Suppose $ L $ is very ample and let $ K _ {A} = {A / {( - 1 ) _ {A} } } $ be the associated Kummer surface. The subvector space $ H ^ {0} ( A,L ) ^ {-} \subset H ^ {0} ( A,L ) $ of odd sections induces an embedding of $ {\widetilde{K} } _ {A} $, the blow-up of $ K _ {A} $ in the $ 16 $ double points, as a smooth quartic surface into $ \mathbf P ^ {3} $. $ {\widetilde{K} } _ {A} \subset \mathbf P ^ {3} $ is invariant under the action of the level- $ 2 $ Heisenberg group (cf. also Heisenberg representation) $ H ( 2,2 ) $. The $ 16 $ blown-up double points become skew lines on the quartic surface. Any $ H ( 2,2 ) $- invariant quartic surface in $ \mathbf P ^ {3} $ with $ 16 $ skew lines comes from a polarized Abelian surface $ ( A, \lambda ) $ of type $ ( 2,6 ) $ in this way (see [a5], [a11] and [a12]).
Type $ ( 3,3 ) $— $ \lambda $ is three times a principal polarization and $ \varphi _ {L} : A \ahR \mathbf P ^ {8} $ is an embedding. If $ ( A, \lambda ) $ is not a product, then the quadrics $ Q \in H ^ {0} ( \mathbf P ^ {8} , {\mathcal I} _ { {A / {\mathbf P ^ {8} } } } ( 2 ) ) $ vanishing on $ A $ generate the ideal sheaf $ {\mathcal I} _ { {A / {\mathbf P ^ {8} } } } $. In the product case, $ {\mathcal I} _ { {A / {\mathbf P ^ {8} } } } $ is generated by quadrics and cubics (see [a4]).
Algebraic completely integrable systems.
An algebraic completely integrable system in the sense of M. Adler and P. van Moerbeke is a completely integrable polynomial Hamiltonian system on $ \mathbf C ^ {N} $( with Casimir functions $ {H _ {1} \dots H _ {k} } : {\mathbf C ^ {N} } \rightarrow \mathbf C $ and $ m = { {( N - k ) } / 2 } $ independent constants of motion $ H _ {k + 1 } \dots H _ {k + m } $ in involution) such that:
a) for a general point $ c = {} ^ {t} ( c _ {1} \dots c _ {k + m } ) \in \mathbf C ^ {k + m } $ the invariant manifold $ A _ {c} ^ {o} = \cap _ {i = 1 } ^ {m + k } \{ H _ {i} = c _ {i} \} \subset \mathbf C ^ {N} $ is an open affine part of an Abelian variety $ A _ {c} $;
b) the flows of the integrable vector fields $ X _ {u _ {i} } $ linearize on the Abelian varieties $ A _ {c} $[a2].
The divisor at infinity $ D _ {c} = A _ {c} - A _ {c} ^ {o} $ defines a polarization on $ A _ {c} $. In this way the mapping $ {( H _ {1} \dots H _ {k + m } ) } : {\mathbf C ^ {N} } \rightarrow {\mathbf C ^ {k + m } } $ defines a family of polarized Abelian varieties (cf. Moduli problem). Some examples of $ 2 $- dimensional algebraic completely integrable systems and their associated Abelian surfaces are:
the three-body Toda lattice and the even, respectively odd, master systems (cf. also Master equations in cooperative and social phenomena) linearize on principally polarized Abelian surfaces;
the Kowalewski top, the Hénon–Heiles system and the Manakov geodesic flow on $ { \mathop{\rm SO} } ( 4 ) $ linearize on Abelian surfaces of type $ ( 1,2 ) $[a1];
the Garnier system linearizes on Abelian surfaces of type $ ( 1,4 ) $[a15].
References
| [a1] | M. Adler, P. van Moerbeke, "The Kowalewski and Hénon–Heiles motions as Manakov geodesic flows on 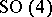 : a two-dimensional family of Lax pairs" Comm. Math. Phys. , 113 (1988) pp. 659–700 : a two-dimensional family of Lax pairs" Comm. Math. Phys. , 113 (1988) pp. 659–700 |
| [a2] | M. Adler, P. van Moerbeke, "The complex geometry of the Kowalewski–Painlevé analysis" Invent. Math. , 97 (1989) pp. 3–51 Zbl 0678.58020 |
| [a3] | W. Barth, "Abelian surfaces with 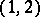 -polarization" , Algebraic Geometry, Sendai, 1985 , Advanced Studies in Pure Math. , 10 (1987) pp. 41–84 MR946234 -polarization" , Algebraic Geometry, Sendai, 1985 , Advanced Studies in Pure Math. , 10 (1987) pp. 41–84 MR946234 |
| [a4] | W. Barth, "Quadratic equations for level- abelian surfaces" , Abelian Varieties, Proc. Workshop Egloffstein 1993 , de Gruyter (1995) pp. 1–18 MR1336597 abelian surfaces" , Abelian Varieties, Proc. Workshop Egloffstein 1993 , de Gruyter (1995) pp. 1–18 MR1336597 |
| [a5] | W. Barth, I. Nieto, "Abelian surfaces of type 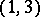 and quartic surfaces with and quartic surfaces with 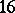 skew lines" J. Algebraic Geom. , 3 (1994) pp. 173–222 MR1257320 Zbl 0809.14027 skew lines" J. Algebraic Geom. , 3 (1994) pp. 173–222 MR1257320 Zbl 0809.14027 |
| [a6] | Ch. Birkenhake, H. Lange, D. van Straten, "Abelian surfaces of type 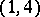 " Math. Ann. , 285 (1989) pp. 625–646 MR1027763 Zbl 0714.14028 " Math. Ann. , 285 (1989) pp. 625–646 MR1027763 Zbl 0714.14028 |
| [a7] | Ch. Birkenhake, H. Lange, "Moduli spaces of Abelian surfaces wih isogeny" , Geometry and Analysis, Bombay Colloquium 1992 , Tata Inst. Fundam. Res. (1995) pp. 225–243 MR1351509 |
| [a8] | G. Horrocks, D. Mumford, "A rank  vector bundle on vector bundle on 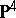 with with 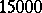 symmetries" Topology , 12 (1973) pp. 63–81 MR382279 Zbl 0255.14017 symmetries" Topology , 12 (1973) pp. 63–81 MR382279 Zbl 0255.14017 |
| [a9] | K. Hulek, H. Lange, "Examples of abelian surfaces in 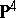 " J. Reine Angew. Math. , 363 (1985) pp. 200–216 MR0814021 Zbl 0593.14027 " J. Reine Angew. Math. , 363 (1985) pp. 200–216 MR0814021 Zbl 0593.14027 |
| [a10] | H. Lange, Ch. Birkenhake, "Complex Abelian varieties" , Grundlehren math. Wiss. , 302 , Springer (1992) MR1217487 Zbl 0779.14012 |
| [a11] | I. Naruki, "On smooth quartic embeddings of Kummer surfaces" Proc. Japan Acad. , 67 A (1991) pp. 223–224 MR1137912 |
| [a12] | V. V. Nikulin, "On Kummer surfaces" Math USSR Izv. , 9 (1975) pp. 261–275 (In Russian) MR429917 Zbl 0325.14015 |
| [a13] | S. Ramanan, "Ample divisors on abelian surfaces" Proc. London Math. Soc. , 51 (1985) pp. 231–245 MR0794112 Zbl 0603.14013 |
| [a14] | I. Reider, "Vector bundles of rank  and linear systems on algebraic surfaces" Ann. of Math. , 127 (1988) pp. 309–316 MR0932299 Zbl 0663.14010 and linear systems on algebraic surfaces" Ann. of Math. , 127 (1988) pp. 309–316 MR0932299 Zbl 0663.14010 |
| [a15] | P. Vanhaecke, "A special case of the Garnier system, 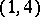 -polarized Abelian surfaces and their moduli" Compositio Math. , 92 (1994) pp. 157–203 MR1283227 -polarized Abelian surfaces and their moduli" Compositio Math. , 92 (1994) pp. 157–203 MR1283227 |
Abelian surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Abelian_surface&oldid=45001