Kodaira dimension
A numerical invariant of an algebraic variety, named after K. Kodaira who first pointed out the importance of this invariant in the theory of the classification of algebraic varieties.
Let $ V $ be a non-singular algebraic variety and let $ \Phi _ {m} : V \rightarrow \mathbf P ( n) $ be a rational mapping defined by a linear system $ | m K _ {V} | $, where $ K _ {V} $ is the canonical class of $ V $. The Kodaira dimension $ \kappa ( V) $ of $ V $ is defined as $ \max _ {m>} 1 \{ \mathop{\rm dim} \Phi _ {m} ( V) \} $. Here, if $ | m K _ {V} | = \emptyset $ for all $ m \geq 1 $, then it is assumed that $ \kappa ( V) = - \infty $. The Kodaira dimension is a birational invariant, that is, it does not depend on the representative in the birational equivalence class.
Suppose that the ground field is the field of the complex numbers $ \mathbf C $. If $ m $ is sufficiently large, then one has the estimate
$$ \alpha m ^ {\kappa ( V) } \leq \mathop{\rm dim} | m K _ {V} | \leq \ \beta m ^ {\kappa ( V) } , $$
where $ \alpha $, $ \beta $ are certain positive numbers. If $ \kappa ( V) > 0 $, then there exists a surjective morphism $ f : V ^ {*} \rightarrow W $ of algebraic varieties such that: a) $ V ^ {*} $ is birationally equivalent to $ V $; b) $ \kappa ( V) = \mathop{\rm dim} W $; and c) for some dense open set $ U \subset W $, all the fibres $ f ^ { - 1 } ( \omega ) $, $ \omega \in U $, are varieties of parabolic type (i.e. of Kodaira dimension zero).
There is a generalization of the notion of the Kodaira dimension (see [2]) to the case when in the linear system $ | m K _ {V} | $ the canonical class $ K _ {V} $ is replaced by an arbitrary divisor $ D $.
References
| [1] | I.R. Shafarevich, "Algebraic surfaces" Proc. Steklov Inst. Math. , 75 (1967) Trudy Mat. Inst. Steklov. , 75 (1965) MR1392959 MR1060325 Zbl 0830.00008 Zbl 0733.14015 Zbl 0832.14026 Zbl 0509.14036 Zbl 0492.14024 Zbl 0379.14006 Zbl 0253.14006 Zbl 0154.21001 |
| [2] | K. Ueno, "Classification theory of algebraic varieties and compact complex spaces" , Springer (1975) MR0506253 Zbl 0299.14007 |
| [3] | S. Iitaka, "On 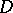 -dimensions of algebraic varieties" J. Math. Soc. Japan , 23 (1971) pp. 356–373 MR285531 -dimensions of algebraic varieties" J. Math. Soc. Japan , 23 (1971) pp. 356–373 MR285531 |
Comments
Let $ X $ be a compact connected complex manifold. Let $ {\mathcal K} _ {X} $ be the canonical bundle on $ X $. There is a canonical pairing of sections
$$ \Gamma ( X, {\mathcal K} _ {X} ^ {\otimes m } ) \otimes \Gamma ( X, {\mathcal K} _ {X} ^ {\otimes n } ) \rightarrow \ \Gamma ( X, {\mathcal K} _ {X} ^ {m + n } ) $$
making $ \mathbf C \oplus \oplus _ {m = 1 } ^ \infty \Gamma ( X, {\mathcal K} _ {X} ^ {m} ) $ into a commutative ring $ R ( X) $, called the canonical ring of $ X $. It can be proved to be of finite transcendence degree, $ \textrm{ tr deg } ( R ( X)) < \infty $. The Kodaira dimension of $ X $ is now described as follows:
$$ \kappa ( X) = - \infty \ \textrm{ if } R ( X) \simeq \mathbf C , $$
$$ \kappa ( X) = \textrm{ tr deg } ( R ( X)) - 1 \ \textrm{ otherwise } . $$
It is always true that $ \kappa ( X) \leq a ( X) \leq \mathop{\rm dim} ( X) $, where $ a ( X) $ is the algebraic dimension of $ X $, i.e. the transcendence degree of the field of meromorphic functions on $ X $. Let $ P _ {m} ( X) = h ^ {0} ( {\mathcal K} _ {X} ^ {\otimes m } ) = \mathop{\rm dim} H ^ {0} ( {\mathcal K} _ {X} ^ {\otimes m } ) $ be the $ m $- th plurigenus of $ X $. Then one has: i) $ \kappa ( X) = - \infty $ if and only if $ P _ {m} ( X) = 0 $ for all $ m \geq 1 $; ii) $ \kappa ( X) = 0 $ if and only if $ P _ {m} ( X) = 0 $ or 1 for $ m \geq 1 $, but not always 0; iii) $ \kappa ( X) = k $, with $ 1 \leq k \leq \mathop{\rm dim} ( X) $, if and only if $ P _ {m} ( X) $ has growth $ m ^ {k} $, i.e. if and only if there exists an integer $ k $ and strictly positive constants $ a $, $ b $ such that $ am ^ {k} \leq P _ {m} ( X) \leq bm ^ {k} $ for large $ m $.
The Kodaira dimension is also called the canonical dimension. For the concept of the logarithmic Kodaira dimension see [a2], Chapt. 11.
References
| [a1] | A. van de Ven, "Compact complex surfaces" , Springer (1984) Zbl 0718.14023 |
| [a2] | S. Iitaka, "Algebraic geometry, an introduction to birational geometry of algebraic varieties" , Springer (1982) pp. Chapt. 10 Zbl 0491.14006 |
Kodaira dimension. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Kodaira_dimension&oldid=47509