Difference between revisions of "Leibniz-Hopf algebra"
m (typo) |
(TeX partially done) |
||
| Line 20: | Line 20: | ||
$$ | $$ | ||
| − | The overlapping shuffle product of two such words | + | The overlapping shuffle product of two such words $u=(a_1,\ldots,a_s)$, $v = (b_1,\ldots,b_t)$ is equal to |
| − | + | $$ | |
| − | + | a \times_{\mathrm{OSh}} b = \sum_{f,g} (c_1,\ldots,c_r) | |
| − | + | $$ | |
| − | where the sum is over all | + | where the sum is over all $r \in \mathbf{N}$ and pairs of order-preserving injective mappings $f : \{1,\ldots,s\} \rightarrow \{1,\ldots,r\}$, $g : \{1,\ldots,t\} \rightarrow \{1,\ldots,r\}$ such that $\mathrm{im}(f) \cup \mathrm{im}(g) = \{1,\ldots,r\}$, and where |
| − | + | $$ | |
| − | + | c_i = a_{f^{-1}(i)} + b_{g^{-1}(i)}\ ,\ \ \ i = 1,\ldots,r | |
| − | + | $$ | |
| − | with | + | with $a_{f^{-1}(i)} = 0 $ if $f^{-1}(i) = \emptyset$ , and similarly for $b_{g^{-1}(i)}$. |
For example, | For example, | ||
Revision as of 18:18, 4 December 2015
Let $\mathbf{Z}\langle Z \rangle$ be the free associative algebra on $Z = \{Z_1,Z_2,\ldots\}$ over the integers. Give $\mathbf{Z}\langle Z \rangle$ a Hopf algebra structure by means of the following co-multiplication, augmentation, and antipode: $$ \mu(Z_n) = \sum_{i+j=n\,;\,\,i,j \ge 0} Z_i \otimes Z_j $$ where $$ Z_0 = 1 $$ $$ \epsilon(Z_n) = 0,\ \ n=1,2,\ldots $$ $$ \iota(Z_n) = \sum_{i_1+\cdots+i_k = n} (-1)^k Z_{i_1} \cdots Z_{i_k} \ , $$ where the sum is over all strings $i_1,\ldots,i_k$, $i_j \ge 1$, such that $i_1+\cdots+i_k = n$. This makes $\mathbf{Z}\langle Z \rangle$ a Hopf algebra, called the Leibniz–Hopf algebra. This Hopf algebra is important, e.g., in the theory of curves of non-commutative formal groups (see Formal group) [a1], [a2], [a5]. Its commutative quotient $\mathbf{Z}[Z]$, with the same co-multiplication, is the underlying Hopf algebra of the (big) Witt vector functor $R \mapsto W(R)$ (see Witt vector) and it plays an important role in the classification theory of unipotent commutative algebraic groups and in the theory of commutative formal groups (amongst other things) [a3].
The Leibniz–Hopf algebra $\mathbf{Z}\langle Z \rangle$ is free as a $\mathbf{Z}$-module and graded. Its graded dual is also a Hopf algebra, whose underlying algebra is the overlapping shuffle algebra $\mathrm{OSh}(\mathbf{N})$. As a $\mathbf Z$-module, $\mathrm{OSh}(\mathbf{N})$ is free with basis $\mathbf{N}^*$, the free monoid (see Free semi-group) of all words in the alphabet $\mathbf{N}$ with the duality pairing $\mathbf{Z}\langle Z \rangle \times \mathrm{OSh}(\mathbf{N}) \rightarrow \mathbf{Z}$ given by $$ \left({ w , Z_{i_1}\cdots Z_{i_r} }\right) = \begin{cases}1,& w = i_1\cdots i_r ,\\ 0 &\text{otherwise}.\end{cases} $$
The overlapping shuffle product of two such words $u=(a_1,\ldots,a_s)$, $v = (b_1,\ldots,b_t)$ is equal to $$ a \times_{\mathrm{OSh}} b = \sum_{f,g} (c_1,\ldots,c_r) $$ where the sum is over all $r \in \mathbf{N}$ and pairs of order-preserving injective mappings $f : \{1,\ldots,s\} \rightarrow \{1,\ldots,r\}$, $g : \{1,\ldots,t\} \rightarrow \{1,\ldots,r\}$ such that $\mathrm{im}(f) \cup \mathrm{im}(g) = \{1,\ldots,r\}$, and where $$ c_i = a_{f^{-1}(i)} + b_{g^{-1}(i)}\ ,\ \ \ i = 1,\ldots,r $$ with $a_{f^{-1}(i)} = 0 $ if $f^{-1}(i) = \emptyset$ , and similarly for $b_{g^{-1}(i)}$.
For example,
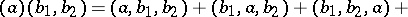 |
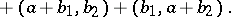 |
The terms of maximal length of the overlapping shuffle product form the shuffle product, see Shuffle algebra.
A word 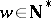 ,
, 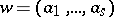 , is elementary if the greatest common divisor of
, is elementary if the greatest common divisor of  is
is 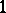 . With this terminology, the Ditters–Scholtens theorem [a4], [a5] says that, as an algebra over
. With this terminology, the Ditters–Scholtens theorem [a4], [a5] says that, as an algebra over 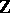 , the overlapping shuffle algebra
, the overlapping shuffle algebra 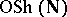 is the free commutative polynomial algebra with as generators the elementary concatenation powers of elementary Lyndon words (see Lyndon word). (E.g., the third concatenation power of
is the free commutative polynomial algebra with as generators the elementary concatenation powers of elementary Lyndon words (see Lyndon word). (E.g., the third concatenation power of 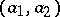 is
is 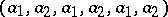 .) In contrast with the case of the shuffle algebra, this theorem already holds over
.) In contrast with the case of the shuffle algebra, this theorem already holds over 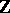 (not just over
(not just over 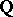 ).
).
References
| [a1] | E.J. Ditters, "Curves and formal (co)groups" Invent. Math. , 17 (1972) pp. 1–20 |
| [a2] | E.J. Ditters, "Groupes formels" , Lecture Notes , Univ. Paris XI: Orsay (1974) |
| [a3] | M. Hazewinkel, "Formal groups and applications" , Acad. Press (1978) MR0506881 MR0463184 Zbl 0454.14020 |
| [a4] | M. Hazewinkel, "The Leibniz Hopf algebra and Lyndon words" Preprint AM CWI , 9612 (1996) |
| [a5] | A.C.J. Scholtens, "$S$-Typical curves in non-commutative Hopf algebras" , Free Univ. Amsterdam (1996) (Thesis) |
References
| [b1] | Michiel Hazewinkel, "The Algebra of Quasi-Symmetric Functions is Free over the Integers", Advances in Mathematics 164 (2001) 283–300 DOI 10.1006/aima.2001.2017 |
Leibniz-Hopf algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Leibniz-Hopf_algebra&oldid=36842