Difference between revisions of "Potential theory"
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
Ulf Rehmann (talk | contribs) m (Undo revision 48266 by Ulf Rehmann (talk)) Tag: Undo |
||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Originally, studies related to the properties of forces which follow the law of gravitation. In the statement of this law given by I. Newton (1687) (cf. [[Newton laws of mechanics|Newton laws of mechanics]]) the only forces considered are the forces of mutual attraction acting upon two material particles of small size or two material points. These forces are directly proportional to the product of the masses of these particles and inversely proportional to the square of the distance between them. Thus, the first and the most important problem from the point of view of celestial mechanics and geodesy was to study the forces of attraction of a material point by a finite smooth material body — a spheroid and, in particular, an ellipsoid (since many celestial bodies have this shape). After first partial achievements by Newton and others, studies carried out by J.L. Lagrange (1773), A. Legendre (1784–1794) and P.S. Laplace (1782–1799) became of major importance. Lagrange has established that a field of gravitational forces, as it is called now, is a [[Potential field|potential field]] and has introduced a function which was later called by G. Green (1828) a potential function and by C.F. Gauss (1840) — just a [[Potential|potential]]. At present, the achievements of this initial period are included in courses on classical celestial mechanics (see also [[#References|[2]]]). | Originally, studies related to the properties of forces which follow the law of gravitation. In the statement of this law given by I. Newton (1687) (cf. [[Newton laws of mechanics|Newton laws of mechanics]]) the only forces considered are the forces of mutual attraction acting upon two material particles of small size or two material points. These forces are directly proportional to the product of the masses of these particles and inversely proportional to the square of the distance between them. Thus, the first and the most important problem from the point of view of celestial mechanics and geodesy was to study the forces of attraction of a material point by a finite smooth material body — a spheroid and, in particular, an ellipsoid (since many celestial bodies have this shape). After first partial achievements by Newton and others, studies carried out by J.L. Lagrange (1773), A. Legendre (1784–1794) and P.S. Laplace (1782–1799) became of major importance. Lagrange has established that a field of gravitational forces, as it is called now, is a [[Potential field|potential field]] and has introduced a function which was later called by G. Green (1828) a potential function and by C.F. Gauss (1840) — just a [[Potential|potential]]. At present, the achievements of this initial period are included in courses on classical celestial mechanics (see also [[#References|[2]]]). | ||
| Line 20: | Line 8: | ||
==Principal classes of potentials and their properties.== | ==Principal classes of potentials and their properties.== | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741401.png" /> be a smooth closed surface, i.e. an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741402.png" />-dimensional smooth manifold without boundary, in the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741403.png" />-dimensional Euclidean space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741404.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741405.png" />, which bounds a bounded domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741406.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741407.png" />. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741408.png" /> be the exterior unbounded domain. Let |
| − | be a smooth closed surface, i.e. an | ||
| − | dimensional smooth manifold without boundary, in the | ||
| − | dimensional Euclidean space | ||
| − | |||
| − | which bounds a bounded domain | ||
| − | |||
| − | Let | ||
| − | be the exterior unbounded domain. Let | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p0741409.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | be a principal [[Fundamental solution|fundamental solution]] of the [[Laplace equation|Laplace equation]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414010.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414011.png" />, where | |
| − | |||
| − | in | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414012.png" /></td> </tr></table> | |
| − | |||
| − | + | is the distance between two points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414013.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414014.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414016.png" /> is the area of the unit sphere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414017.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414018.png" /> is the gamma-function. The following three integrals, which depend on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414019.png" /> as a parameter, | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414020.png" /></td> <td valign="top" style="width:5%;text-align:right;">(1)</td></tr></table> | |
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414021.png" /> is the direction of the exterior (with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414022.png" />) normal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414023.png" /> at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414024.png" />, are called the volume potential, the single-layer potential and the double-layer potential, respectively. The functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414027.png" /> are called the densities of the corresponding potentials; hereafter they are assumed to be absolutely integrable over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414028.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414029.png" />, respectively. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414030.png" /> (and sometimes for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414031.png" />) the integrals (1) are called the Newton volume potential and the Newton single- and double-layer potentials; for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414032.png" /> they are called logarithmic mass, single-layer or double-layer potentials, respectively. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414033.png" /> be of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414034.png" />. Then the volume potential (cf. [[Newton potential|Newton potential]]) and its first derivatives are continuous everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414035.png" />; moreover, they can be calculated by differentiation under the integral sign, i.e. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414036.png" />. Further, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414037.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The second derivatives are continuous everywhere outside <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414038.png" />, but they have a discontinuity when passing across the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414039.png" />; moreover, in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414040.png" /> they satisfy the [[Poisson equation|Poisson equation]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414041.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414042.png" />, and in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414043.png" /> — the Laplace equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414044.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414045.png" />. The above-mentioned properties characterize a volume potential. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414046.png" /> is a bounded domain in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414047.png" /> with boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414048.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414049.png" />, then Gauss' formula for a volume potential is valid: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414050.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414051.png" />. The single-layer potential (cf. [[Simple-layer potential|Simple-layer potential]]) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414052.png" /> is a harmonic function when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414053.png" />; moreover, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414054.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | in particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414055.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414056.png" />, but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414057.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414058.png" /> if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414059.png" />. A single-layer potential is continuous everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414060.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414061.png" />, moreover, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414062.png" /> and its tangential derivatives are continuous when passing across the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414063.png" />. The normal derivative of a single-layer potential has a discontinuity when passing across the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414064.png" />: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414065.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414066.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414067.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414068.png" /> are the limit values of the normal derivative from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414069.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414070.png" />, respectively, i.e. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414071.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414072.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414073.png" /> denotes the so-called direct value of the normal derivative of a single-layer potential calculated over the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414074.png" />, i.e. | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414075.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | It is a continuous function of the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414076.png" />, and the kernel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414077.png" /> has a weak singularity on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414078.png" />, | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414079.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
These properties characterize a single-layer potential. | These properties characterize a single-layer potential. | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414080.png" />. The [[Double-layer potential|double-layer potential]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414081.png" /> is a harmonic function for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414082.png" />; moreover, |
| − | The [[Double-layer potential|double-layer potential]] | ||
| − | is a harmonic function for | ||
| − | moreover, | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414083.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | When passing across the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414084.png" /> the double-layer potential has a discontinuity (whence its name): | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414085.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414086.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414087.png" /> are the limit values of the double-layer potential from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414088.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414089.png" />, respectively, that is, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414090.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414091.png" /> when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414092.png" /> denotes the so-called direct value of the double-layer potential calculated over the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414093.png" />, that is, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414094.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | It is a continuous function of the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414095.png" />, and the kernel <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414096.png" /> has a weak singularity on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414097.png" />, | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414098.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | The tangential derivatives of a double-layer potential also have a discontinuity when passing across the surface | + | The tangential derivatives of a double-layer potential also have a discontinuity when passing across the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p07414099.png" />, but the normal derivative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140100.png" /> retains its value when passing across <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140101.png" />: |
| − | but the normal derivative | ||
| − | retains its value when passing across | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140102.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
These properties characterize a double-layer potential. | These properties characterize a double-layer potential. | ||
| − | In the case of a constant density | + | In the case of a constant density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140103.png" /> Gauss' formula for a double-layer potential holds: |
| − | Gauss' formula for a double-layer potential holds: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140104.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The integral at the left-hand side of this equality is interpreted (when divided by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140105.png" />) as the solid angle at which the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140106.png" /> is seen from the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140107.png" />. | |
| − | + | Below, certain properties of potentials under weaker restrictions on the densities and the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140108.png" /> are given. | |
| − | |||
| − | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140109.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140110.png" /> is a harmonic function for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140111.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140112.png" /> is summable on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140113.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140114.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140115.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140116.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140117.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140118.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140119.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140120.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140121.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140122.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140123.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140124.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140125.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140126.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140127.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140128.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140129.png" />, then the generalized second derivatives of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140130.png" /> exist, they are also of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140131.png" /> and are expressed by singular integrals: | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140132.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140133.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140134.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140135.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140136.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140137.png" />; if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140138.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140139.png" />, then all generalized derivatives <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140140.png" /> also exist and belong to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140141.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140142.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140143.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140144.png" /> is a generalized solution of the Poisson equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140145.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140146.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140147.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140148.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140149.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140150.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140151.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140152.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140153.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140154.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140155.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140156.png" /> integers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140157.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140158.png" />. |
| − | for | ||
| − | |||
| − | for | ||
| − | if | ||
| − | |||
| − | then all generalized derivatives | ||
| − | also exist and belong to | ||
| − | If | ||
| − | |||
| − | then | ||
| − | is a generalized solution of the Poisson equation | ||
| − | |||
| − | If | ||
| − | and | ||
| − | |||
| − | then | ||
| − | |||
| − | or | ||
| − | If | ||
| − | and | ||
| − | |||
| − | |||
| − | integers, | ||
| − | then | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140159.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140160.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140161.png" /> be a closed bounded domain such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140162.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140163.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140164.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140165.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140166.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140167.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140168.png" />; <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140169.png" />. If the density is bounded and summable, then |
| − | |||
| − | let | ||
| − | be a closed bounded domain such that | ||
| − | If | ||
| − | |||
| − | then | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | If the density is bounded and summable, then | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140170.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140171.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140172.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140173.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140174.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140175.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140176.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140177.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140178.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140179.png" />. |
| − | |||
| − | then | ||
| − | |||
| − | or | ||
| − | If | ||
| − | then | ||
| − | |||
| − | or | ||
| − | If | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140180.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140181.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140182.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140183.png" /> integers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140184.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140185.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140186.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140187.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140188.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140189.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140190.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140191.png" /> integers, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140192.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140193.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140194.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140195.png" />. |
| − | and | ||
| − | |||
| − | |||
| − | integers, | ||
| − | then | ||
| − | |||
| − | or | ||
| − | If | ||
| − | and | ||
| − | |||
| − | |||
| − | integers, | ||
| − | then | ||
| − | |||
| − | or | ||
| − | For potentials and their derivatives extended by continuity on | + | For potentials and their derivatives extended by continuity on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140196.png" /> the above-described properties of smoothness are also valid under the corresponding smoothness conditions on the density and the surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140197.png" />. |
| − | the above-described properties of smoothness are also valid under the corresponding smoothness conditions on the density and the surface | ||
==Representation of functions and solution of the principal boundary value problems in potential theory using potentials.== | ==Representation of functions and solution of the principal boundary value problems in potential theory using potentials.== | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140198.png" /> be a function of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140199.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140200.png" /> be a smooth surface of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140201.png" />. Then the following integral identity (Green formula) holds: |
| − | be a function of class | ||
| − | and let | ||
| − | be a smooth surface of class | ||
| − | Then the following integral identity (Green formula) holds: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140202.png" /></td> <td valign="top" style="width:5%;text-align:right;">(2)</td></tr></table> | |
| − | - | ||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140203.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | In particular, in | + | In particular, in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140204.png" /> the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140205.png" /> can be represented as the sum of a volume potential and single- and double-layer potentials, with respective densities |
| − | the function | ||
| − | can be represented as the sum of a volume potential and single- and double-layer potentials, with respective densities | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140206.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | For a function | + | For a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140207.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140208.png" /> that is harmonic on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140209.png" /> the following identity holds: |
| − | of class | ||
| − | that is harmonic on | ||
| − | the following identity holds: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140210.png" /></td> <td valign="top" style="width:5%;text-align:right;">(3)</td></tr></table> | |
| − | |||
| − | |||
| − | + | Hence, such a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140211.png" /> can be represented in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140212.png" /> by the sum of single- and double-layer potentials with densities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140213.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140214.png" />, respectively. However, the densities in (3) cannot be arbitrarily given on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140215.png" />; they are connected by the integral relation obtained from (3) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140216.png" />. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | A central place in potential theory is occupied by the Dirichlet and the Neumann boundary value problem (also called the first and the second boundary value problem (cf. also [[Dirichlet problem|Dirichlet problem]]; [[Neumann problem]])) for the domains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140217.png" /> (interior problems) and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140218.png" /> (exterior problems) which, under the assumption of sufficient smoothness, can be completely studied by reducing them to the integral equations of potential theory. | |
| − | |||
| − | by the | ||
| − | |||
| − | |||
| − | |||
| − | + | The interior Dirichlet problem: Find a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140219.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140220.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140221.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140222.png" />, harmonic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140223.png" />, which satisfies the boundary condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140224.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140225.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140226.png" /> is a given continuous function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140227.png" />. The solution to this problem always exists, is unique and can be obtained in the form of a double-layer potential | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140228.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140229.png" /> which is obtained as the unique solution of the Fredholm integral equation of the second kind | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140230.png" /></td> </tr></table> | |
| − | |||
| − | + | The interior Neumann problem: Find a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140231.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140232.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140233.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140234.png" />, harmonic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140235.png" />, which satisfies the boundary condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140236.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140237.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140238.png" /> is a given continuous function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140239.png" />. A solution to this problem exists if and only if the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140240.png" /> satisfies the orthogonality condition | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140241.png" /></td> <td valign="top" style="width:5%;text-align:right;">(4)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | This solution is obtained up to an arbitrary additive constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140242.png" /> in the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140243.png" />, where | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140244.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | is a single-layer potential whose density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140245.png" /> is obtained from the following Fredholm integral equation of the second kind: | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140246.png" /></td> <td valign="top" style="width:5%;text-align:right;">(5)</td></tr></table> | |
| − | |||
| − | + | The continuous homogeneous equation has a non-trivial solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140247.png" /> and the inhomogeneous equation (5) is solvable under the condition (4); moreover, its general solution has the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140248.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140249.png" /> is an arbitrary constant. | |
| − | + | The exterior Dirichlet problem: Find a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140250.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140251.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140252.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140253.png" />, harmonic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140254.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140255.png" />, which satisfies the boundary condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140256.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140257.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140258.png" /> is a given continuous function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140259.png" />. Here, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140260.png" /> is assumed to be regular at infinity, i.e. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140261.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The solution of this problem always exists, is unique and can be obtained in the form | The solution of this problem always exists, is unique and can be obtained in the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140262.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140263.png" /> is a constant and |
| − | is a constant and | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140264.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | is a double-layer potential whose density | + | is a double-layer potential whose density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140265.png" /> is a solution of the following Fredholm integral equation of the second kind: |
| − | is a solution of the following Fredholm integral equation of the second kind: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140266.png" /></td> <td valign="top" style="width:5%;text-align:right;">(6)</td></tr></table> | |
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140267.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The corresponding homogeneous equation has the non-trivial solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140268.png" />. Under an adequate choice of the constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140269.png" />, the solution of the inhomogeneous equation (6) takes the form | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140270.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140271.png" /> is an arbitrary constant and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140272.png" /> is a particular solution of (6). The constant <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140273.png" /> is chosen in the form | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140274.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | where the density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140275.png" /> must satisfy the condition | |
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140276.png" /></td> <td valign="top" style="width:5%;text-align:right;">(7)</td></tr></table> | |
| − | |||
| − | + | This density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140277.png" /> is a non-trivial solution of the equation (5) of the interior Neumann problem with data <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140278.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140279.png" />, satisfying the normalization condition | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140280.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | which is equivalent to (7) for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140281.png" />. The single-layer potential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140282.png" /> with density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140283.png" /> is called an equilibrium potential or Robin potential. The density <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140284.png" /> provides a solution to the [[Robin problem|Robin problem]] or the electrostatic problem on the distribution of charges on the conductor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140285.png" /> generating a constant equilibrium potential in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140286.png" />. A certain complexity in solving the exterior Dirichlet problem is due to the fact that, in general, the harmonic function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140287.png" /> that is regular at infinity decreases slower than the double-layer potential as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140288.png" /> and, thus, in the general case <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140289.png" /> cannot be represented only by one double-layer potential. | |
| − | |||
| − | |||
| − | |||
| − | + | The exterior Neumann problem: Find a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140290.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140291.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140292.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140293.png" />, harmonic in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140294.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140295.png" />, which satisfies the boundary condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140296.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140297.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140298.png" /> is a given continuous function on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140299.png" />; in addition, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140300.png" /> is assumed to be regular at infinity. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140301.png" /> the solution of this problem always exists and is unique; for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140302.png" /> a solution exists if and only if the following condition holds: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | and | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140303.png" /></td> <td valign="top" style="width:5%;text-align:right;">(8)</td></tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Moreover, this solution is defined up to an arbitrary additive constant. This solution of the exterior Neumann problem can be represented in the form of a single-layer potential | Moreover, this solution is defined up to an arbitrary additive constant. This solution of the exterior Neumann problem can be represented in the form of a single-layer potential | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140304.png" /></td> </tr></table> | |
| − | |||
| − | |||
whose density is a solution of the following Fredholm integral equation of the second kind: | whose density is a solution of the following Fredholm integral equation of the second kind: | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140305.png" /></td> <td valign="top" style="width:5%;text-align:right;">(9)</td></tr></table> | |
| − | - | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | For | + | For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140306.png" /> the solution of this equation always exists and is unique. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140307.png" /> the corresponding homogeneous equation has a non-trivial solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140308.png" />. Thus, the inhomogeneous equation (9) with the solvability condition (8) has a unique solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140309.png" /> such that |
| − | the solution of this equation always exists and is unique. For | ||
| − | the corresponding homogeneous equation has a non-trivial solution | ||
| − | Thus, the inhomogeneous equation (9) with the solvability condition (8) has a unique solution | ||
| − | such that | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140310.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | and its general solution is of the form | + | and its general solution is of the form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140311.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140312.png" /> is an arbitrary constant. |
| − | where | ||
| − | is an arbitrary constant. | ||
Boundary value problems in potential theory can also be solved using a [[Green function|Green function]]. For instance, for the (interior) Dirichlet problem the Green function has the form | Boundary value problems in potential theory can also be solved using a [[Green function|Green function]]. For instance, for the (interior) Dirichlet problem the Green function has the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140313.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | where | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140314.png" /> is a harmonic function in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140315.png" /> that is continuous with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140316.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140317.png" /> and that satisfies, for each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140318.png" />, the boundary condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140319.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140320.png" />. The solution of the (interior) Dirichlet problem <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140321.png" /> of class <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140322.png" /> for the Poisson equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140323.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140324.png" />, with the boundary condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140325.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140326.png" />, can be represented in the form |
| − | is a harmonic function in | ||
| − | that is continuous with respect to | ||
| − | on | ||
| − | and that satisfies, for each | ||
| − | the boundary condition | ||
| − | |||
| − | The solution of the (interior) Dirichlet problem | ||
| − | of class | ||
| − | for the Poisson equation | ||
| − | |||
| − | with the boundary condition | ||
| − | |||
| − | can be represented in the form | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140327.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
The integrals | The integrals | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140328.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | + | which depend on the parameter <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140329.png" />, are called the Green volume potential (of the Dirichlet problem) and the Green double-layer potential, respectively. Their properties are similar to the properties of the potentials (1). | |
| − | |||
| − | + | Green functions allow one to reduce eigen value problems to integral equations. For instance, the Dirichlet problem <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140330.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140331.png" />, with boundary condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140332.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140333.png" />, is reduced to the following Fredholm integral equation of the second kind with a self-adjoint kernel: | |
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140334.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Further generalization of some fundamental concepts in potential theory.== | ==Further generalization of some fundamental concepts in potential theory.== | ||
Simultaneously with profound studies on the properties of the potentials (1), defined by densities of a more or less general form, and of their applications, the concept of potential itself has undergone a deep generalization related to the concepts of a [[Radon measure|Radon measure]] and a Radon integral. This process started in the 1920s. | Simultaneously with profound studies on the properties of the potentials (1), defined by densities of a more or less general form, and of their applications, the concept of potential itself has undergone a deep generalization related to the concepts of a [[Radon measure|Radon measure]] and a Radon integral. This process started in the 1920s. | ||
| − | Let | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140335.png" /> be a positive [[Borel measure|Borel measure]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140336.png" /> with compact support <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140337.png" />. The potential of the measure, |
| − | be a positive [[Borel measure|Borel measure]] on | ||
| − | with compact support | ||
| − | The potential of the measure, | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140338.png" /></td> <td valign="top" style="width:5%;text-align:right;">(10)</td></tr></table> | |
| − | |||
| − | |||
| − | exists everywhere in | + | exists everywhere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140339.png" /> in the sense of a mapping <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140340.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140341.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140342.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140343.png" /> (i.e. here the value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140344.png" /> is also allowed), is a [[Superharmonic function|superharmonic function]] everywhere in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140345.png" /> and is harmonic outside the support <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140346.png" />. For a measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140347.png" /> of arbitrary sign with compact support the potential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140348.png" /> is defined on the basis of the canonical decomposition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140349.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140350.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140351.png" />, as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140352.png" />. At the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140353.png" /> where both potentials <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140354.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140355.png" /> assume the value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140356.png" />, this potential is not defined. If the measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140357.png" /> is concentrated on a smooth surface <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140358.png" />, then the double-layer potential of the measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140359.png" /> is determined similarly to (10): |
| − | in the sense of a mapping | ||
| − | |||
| − | and | ||
| − | for | ||
| − | i.e. here the value | ||
| − | is also allowed), is a [[Superharmonic function|superharmonic function]] everywhere in | ||
| − | and is harmonic outside the support | ||
| − | For a measure | ||
| − | of arbitrary sign with compact support the potential | ||
| − | is defined on the basis of the canonical decomposition | ||
| − | |||
| − | |||
| − | as | ||
| − | At the points | ||
| − | where both potentials | ||
| − | and | ||
| − | assume the value | ||
| − | this potential is not defined. If the measure | ||
| − | is concentrated on a smooth surface | ||
| − | then the double-layer potential of the measure | ||
| − | is determined similarly to (10): | ||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140360.png" /></td> </tr></table> | |
| − | + | The potential (10) is finite, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140361.png" /> everywhere on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140362.png" /> except at the points of a [[Polar set|polar set]], which is characterized as a set of outer [[Capacity|capacity]] zero. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140363.png" /> everywhere except on a set of outer capacity zero, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140364.png" />. If the measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140365.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140366.png" />, is concentrated on a set of capacity zero, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140367.png" />. The following maximum principle is valid: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140368.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | i.e. the least upper bound of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140369.png" /> equals the least upper bound of the restriction of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140370.png" /> to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140371.png" />. If this restriction is continuous (in the general case, including <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140372.png" />) at a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140373.png" />, then the potential <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140374.png" /> is continuous at that point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140375.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140376.png" />. The potentials of a measure, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140377.png" />, can be reduced to potentials of densities (1) if and only if the measure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140378.png" /> is absolutely continuous with respect to the Lebesgue measure in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140379.png" /> or on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140380.png" />, respectively (see [[#References|[3]]]–[[#References|[6]]]). | |
| − | |||
| − | |||
| − | , | ||
| − | |||
| − | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140381.png" /> is a [[Generalized function|generalized function]], or distribution, on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140382.png" />, then its potential is defined as the convolution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140383.png" />, which is also a generalized function. For instance, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140384.png" /> is a generalized function with compact support, then the Poisson equation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140385.png" /> is valid on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140386.png" /> in the sense of the theory of generalized functions. Potentials of measures can be considered as a particular case of potentials of distributions. For potentials of distributions see [[#References|[3]]], [[#References|[4]]], [[#References|[9]]]. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | then the | ||
| − | is | ||
| − | in | ||
| − | |||
| − | can be | ||
| − | |||
| − | |||
| − | |||
| − | + | For domains <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140387.png" /> with sufficiently smooth boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140388.png" /> the method of potentials provides an efficient solution to the Dirichlet problem. One of the principal directions of development in potential theory consists in finding methods to prove the existence and uniqueness of a solution to the Dirichlet problem for wider classes of domains (see [[Balayage method|Balayage method]]; [[Dirichlet principle|Dirichlet principle]]; [[Perron method|Perron method]]; [[Schwarz alternating method|Schwarz alternating method]]). However, in 1910 S. Zaremba noted that for a plane domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140389.png" /> whose boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140390.png" /> has isolated points the Dirichlet problem is not always solvable in the above classical formulation; in addition, in 1912 H. Lebesgue has shown that it is not always solvable also for spatial domains homeomorphic to a closed sphere but with a sufficiently sharp edge at the boundary entering inside the domain (a so-called Lebesgue spine, see [[Irregular boundary point|Irregular boundary point]]), i.e. there exist continuous functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140391.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140392.png" />, for which the Dirichlet problem cannot be solved in any way. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Thus, the generalized Perron–Wiener solution to the Dirichlet problem for the Laplace equation obtained in the course of development of the Perron method is of great importance. As has been shown by N. Wiener (1924), in this case any finite continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140393.png" /> prescribed on the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140394.png" /> of an arbitrary bounded domain <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140395.png" /> is resolutive, i.e. the generalized Perron–Wiener solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140396.png" /> for this function exists and, moreover, is unique. In general, in 1939 M. Brelot has shown that a finite measurable function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140397.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140398.png" /> is resolutive if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140399.png" /> is integrable with respect to [[Harmonic measure|harmonic measure]] on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140400.png" />. | |
| − | |||
| − | the | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | The generalized solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140401.png" /> does not take the prescribed values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140402.png" /> at all boundary points. A point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140403.png" /> is called a regular point if for any finite continuous function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140404.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140405.png" /> the generalized solution <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140406.png" /> takes the value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140407.png" />, that is, | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | is | ||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140408.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | All other points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140409.png" /> are called irregular points; they include the isolated points of the boundary when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140410.png" /> and the Lebesgue spine for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140411.png" />. It turned out (the [[Kellogg–Evans theorem|Kellogg–Evans theorem]], 1933) that the set of irregular points has outer capacity zero, i.e. this set is in some sense thin. The set of regular points is dense in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140412.png" />. | |
| − | |||
| − | |||
| − | |||
| − | + | For the Dirichlet problem one can construct a generalized Green function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140413.png" />, which can be defined, e.g., for an arbitrary fixed point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140414.png" /> in the following way: | |
| − | |||
| − | |||
| − | |||
| − | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140415.png" /></td> </tr></table> | |
| − | |||
| − | |||
| − | + | The generalized Green function preserves some properties of the classical Green function, for example, the symmetry property <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140416.png" />, but <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140417.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140418.png" />, if and only if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140419.png" /> is a regular point of the boundary <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140420.png" /> (see [[#References|[4]]], [[#References|[6]]]). | |
| − | |||
| − | |||
| − | |||
| − | + | The studies of potentials with other kernels, different from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p074/p074140/p074140421.png" />, and the study of the Dirichlet problem for compacta and the stability of the Dirichlet problem are of great importance (see [[#References|[6]]], [[#References|[4]]]). Their application to the solution of boundary value problems is intensively developed (see [[Bessel potential|Bessel potential]]; [[Non-linear potential|Non-linear potential]]; [[Riesz potential|Riesz potential]]; and also [[#References|[3]]], [[#References|[11]]]). | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The studies of potentials with other kernels, different from | ||
| − | and the study of the Dirichlet problem for compacta and the stability of the Dirichlet problem are of great importance (see [[#References|[6]]], [[#References|[4]]]). Their application to the solution of boundary value problems is intensively developed (see [[Bessel potential|Bessel potential]]; [[Non-linear potential|Non-linear potential]]; [[Riesz potential|Riesz potential]]; and also [[#References|[3]]], [[#References|[11]]]). | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.M. [N.M. Gyunter] Günter, "Potential theory and its application to basic problems of mathematical physics" , F. Ungar (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.N. Sretenskii, "Theory of the Newton potential" , Moscow-Leningrad (1946) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.V. Keldysh, "On the resolutivity and the stability of the Dirichlet problem" ''Uspekhi Mat. Nauk'' , '''8''' (1941) pp. 171–231 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.S. Vladimirov, "Equations of mathematical physics" , M. Dekker (1971) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> S.G. Mikhlin, "Linear partial differential equations" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian)</TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N.M. [N.M. Gyunter] Günter, "Potential theory and its application to basic problems of mathematical physics" , F. Ungar (1967) (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.N. Sretenskii, "Theory of the Newton potential" , Moscow-Leningrad (1946) (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> M.V. Keldysh, "On the resolutivity and the stability of the Dirichlet problem" ''Uspekhi Mat. Nauk'' , '''8''' (1941) pp. 171–231 (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> V.S. Vladimirov, "Equations of mathematical physics" , M. Dekker (1971) (Translated from Russian)</TD></TR><TR><TD valign="top">[10]</TD> <TD valign="top"> R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , '''2''' , Interscience (1965) (Translated from German)</TD></TR><TR><TD valign="top">[11]</TD> <TD valign="top"> C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian)</TD></TR><TR><TD valign="top">[12]</TD> <TD valign="top"> S.G. Mikhlin, "Linear partial differential equations" , Moscow (1977) (In Russian)</TD></TR><TR><TD valign="top">[13]</TD> <TD valign="top"> A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian)</TD></TR></table> | ||
| + | |||
| + | |||
====Comments==== | ====Comments==== | ||
Revision as of 14:52, 7 June 2020
Originally, studies related to the properties of forces which follow the law of gravitation. In the statement of this law given by I. Newton (1687) (cf. Newton laws of mechanics) the only forces considered are the forces of mutual attraction acting upon two material particles of small size or two material points. These forces are directly proportional to the product of the masses of these particles and inversely proportional to the square of the distance between them. Thus, the first and the most important problem from the point of view of celestial mechanics and geodesy was to study the forces of attraction of a material point by a finite smooth material body — a spheroid and, in particular, an ellipsoid (since many celestial bodies have this shape). After first partial achievements by Newton and others, studies carried out by J.L. Lagrange (1773), A. Legendre (1784–1794) and P.S. Laplace (1782–1799) became of major importance. Lagrange has established that a field of gravitational forces, as it is called now, is a potential field and has introduced a function which was later called by G. Green (1828) a potential function and by C.F. Gauss (1840) — just a potential. At present, the achievements of this initial period are included in courses on classical celestial mechanics (see also [2]).
Already Gauss and his contemporaries discovered that the method of potentials (cf. Potentials, method of) can be applied not only to solve problems in the theory of gravitation but, in general, to solve a wide range of problems in mathematical physics, in particular in electrostatics and magnetism. In this connection, potentials became to be considered not only for the physically realistic problems concerning the mutual attraction of positive masses, but also for problems with "masses" of arbitrary sign, or charges. The principal boundary value problems were defined, such as the Dirichlet problem and the Neumann problem, the electrostatic problem of the static distribution of charges on conductors or the Robin problem, and the problem of sweeping-out mass (see Balayage method). To solve the above-mentioned problems in the case of domains with sufficiently smooth boundaries certain types of potentials turned out to be efficient, i.e. special classes of parameter-dependent integrals such as volume potentials of distributed mass, single- and double-layer potentials, logarithmic potentials, Green potentials, etc. Results obtained by A.M. Lyapunov and V.A. Steklov at the end of the 19th century were fundamental for the creation of strong methods of solution of the principal boundary value problems. Studies in potential theory concerning properties of different potentials have acquired an independent significance.
In the first half of the 20th century, a great stimulus for the generalization of the principal problems and the completion of the existing formulations in potential theory was made on the basis of the general notions of a Radon measure, a capacity and generalized functions. Modern potential theory is closely related in its development to the theory of analytic, harmonic and subharmonic functions and to probability theory.
Together with further profound studies of classical boundary value problems and inverse problems (see Potential theory, inverse problems in) the modern period in the development of potential theory is characterized by the application of methods and notions of topology and functional analysis, and the use of abstract axiomatic methods (see Potential theory, abstract).
Principal classes of potentials and their properties.
Let 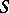 be a smooth closed surface, i.e. an
be a smooth closed surface, i.e. an 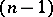 -dimensional smooth manifold without boundary, in the
-dimensional smooth manifold without boundary, in the  -dimensional Euclidean space
-dimensional Euclidean space 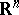 ,
, 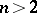 , which bounds a bounded domain
, which bounds a bounded domain 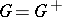 ,
, 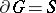 . Let
. Let 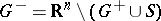 be the exterior unbounded domain. Let
be the exterior unbounded domain. Let
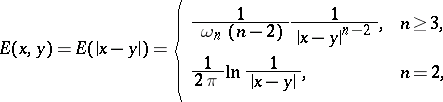 |
be a principal fundamental solution of the Laplace equation 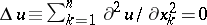 in
in  , where
, where
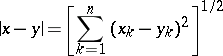 |
is the distance between two points 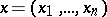 and
and 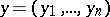 in
in 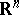 ,
, 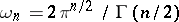 is the area of the unit sphere in
is the area of the unit sphere in 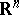 and
and  is the gamma-function. The following three integrals, which depend on
is the gamma-function. The following three integrals, which depend on  as a parameter,
as a parameter,
 | (1) |
where 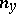 is the direction of the exterior (with respect to
is the direction of the exterior (with respect to 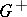 ) normal to
) normal to 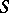 at a point
at a point 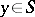 , are called the volume potential, the single-layer potential and the double-layer potential, respectively. The functions
, are called the volume potential, the single-layer potential and the double-layer potential, respectively. The functions 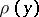 ,
, 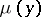 and
and 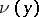 are called the densities of the corresponding potentials; hereafter they are assumed to be absolutely integrable over
are called the densities of the corresponding potentials; hereafter they are assumed to be absolutely integrable over 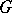 or
or 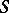 , respectively. For
, respectively. For 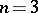 (and sometimes for
(and sometimes for 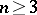 ) the integrals (1) are called the Newton volume potential and the Newton single- and double-layer potentials; for
) the integrals (1) are called the Newton volume potential and the Newton single- and double-layer potentials; for  they are called logarithmic mass, single-layer or double-layer potentials, respectively. Let
they are called logarithmic mass, single-layer or double-layer potentials, respectively. Let 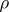 be of class
be of class 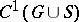 . Then the volume potential (cf. Newton potential) and its first derivatives are continuous everywhere on
. Then the volume potential (cf. Newton potential) and its first derivatives are continuous everywhere on 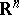 ; moreover, they can be calculated by differentiation under the integral sign, i.e.
; moreover, they can be calculated by differentiation under the integral sign, i.e. 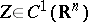 . Further,
. Further,
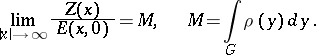 |
The second derivatives are continuous everywhere outside 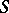 , but they have a discontinuity when passing across the surface
, but they have a discontinuity when passing across the surface 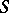 ; moreover, in
; moreover, in 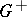 they satisfy the Poisson equation
they satisfy the Poisson equation 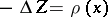 ,
, 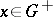 , and in
, and in 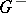 — the Laplace equation
— the Laplace equation 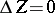 ,
, 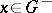 . The above-mentioned properties characterize a volume potential.
. The above-mentioned properties characterize a volume potential.
If 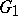 is a bounded domain in
is a bounded domain in 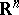 with boundary
with boundary 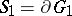 of class
of class 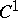 , then Gauss' formula for a volume potential is valid:
, then Gauss' formula for a volume potential is valid:
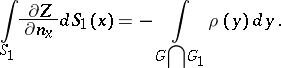 |
Let 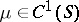 . The single-layer potential (cf. Simple-layer potential)
. The single-layer potential (cf. Simple-layer potential) 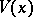 is a harmonic function when
is a harmonic function when 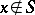 ; moreover,
; moreover,
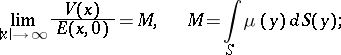 |
in particular, 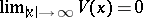 for
for 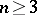 , but
, but 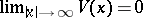 when
when 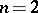 if and only if
if and only if 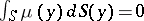 . A single-layer potential is continuous everywhere on
. A single-layer potential is continuous everywhere on 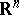 ,
, 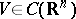 , moreover,
, moreover, 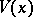 and its tangential derivatives are continuous when passing across the surface
and its tangential derivatives are continuous when passing across the surface 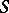 . The normal derivative of a single-layer potential has a discontinuity when passing across the surface
. The normal derivative of a single-layer potential has a discontinuity when passing across the surface  :
:
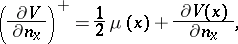 |
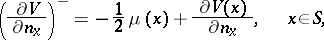 |
where 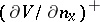 and
and 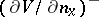 are the limit values of the normal derivative from
are the limit values of the normal derivative from 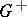 and
and  , respectively, i.e.
, respectively, i.e.
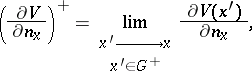 |
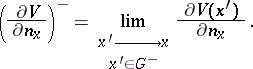 |
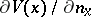 denotes the so-called direct value of the normal derivative of a single-layer potential calculated over the surface
denotes the so-called direct value of the normal derivative of a single-layer potential calculated over the surface 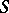 , i.e.
, i.e.
 |
It is a continuous function of the points 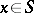 , and the kernel
, and the kernel 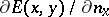 has a weak singularity on
has a weak singularity on 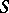 ,
,
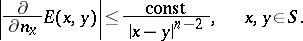 |
These properties characterize a single-layer potential.
Let 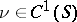 . The double-layer potential
. The double-layer potential 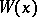 is a harmonic function for
is a harmonic function for 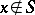 ; moreover,
; moreover,
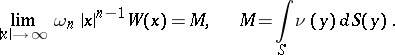 |
When passing across the surface 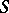 the double-layer potential has a discontinuity (whence its name):
the double-layer potential has a discontinuity (whence its name):
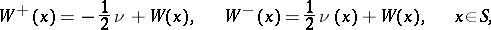 |
where 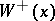 and
and 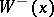 are the limit values of the double-layer potential from
are the limit values of the double-layer potential from 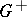 and
and 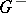 , respectively, that is,
, respectively, that is,
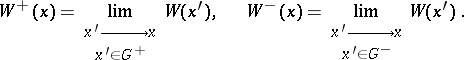 |
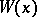 when
when 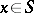 denotes the so-called direct value of the double-layer potential calculated over the surface
denotes the so-called direct value of the double-layer potential calculated over the surface 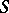 , that is,
, that is,
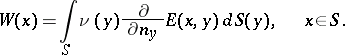 |
It is a continuous function of the points 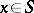 , and the kernel
, and the kernel 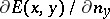 has a weak singularity on
has a weak singularity on 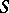 ,
,
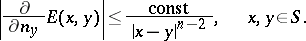 |
The tangential derivatives of a double-layer potential also have a discontinuity when passing across the surface 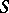 , but the normal derivative
, but the normal derivative 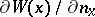 retains its value when passing across
retains its value when passing across 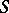 :
:
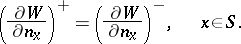 |
These properties characterize a double-layer potential.
In the case of a constant density 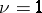 Gauss' formula for a double-layer potential holds:
Gauss' formula for a double-layer potential holds:
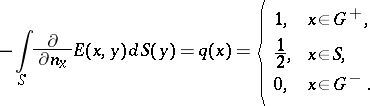 |
The integral at the left-hand side of this equality is interpreted (when divided by 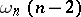 ) as the solid angle at which the surface
) as the solid angle at which the surface  is seen from the point
is seen from the point  .
.
Below, certain properties of potentials under weaker restrictions on the densities and the surface 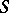 are given.
are given.
If 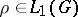 , then
, then 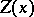 is a harmonic function for
is a harmonic function for 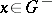 and
and 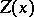 is summable on
is summable on 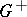 . If
. If 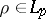 ,
,  , then
, then 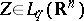 ,
, 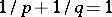 ,
, 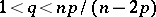 ; if
; if 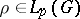 ,
, 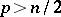 , then
, then  . If
. If 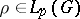 ,
, 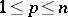 , then
, then 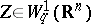 ,
, 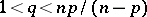 ; if
; if 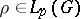 ,
, 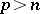 , then
, then 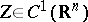 . If
. If 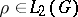 , then the generalized second derivatives of
, then the generalized second derivatives of 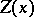 exist, they are also of class
exist, they are also of class 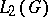 and are expressed by singular integrals:
and are expressed by singular integrals:
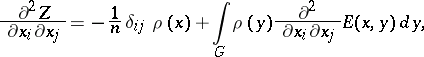 |
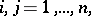 |
where 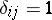 for
for  ,
, 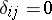 for
for 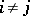 ; if
; if  ,
, 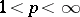 , then all generalized derivatives
, then all generalized derivatives 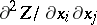 also exist and belong to
also exist and belong to 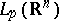 . If
. If 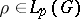 ,
, 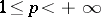 , then
, then 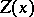 is a generalized solution of the Poisson equation
is a generalized solution of the Poisson equation 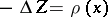 ,
, 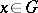 . If
. If 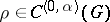 and
and 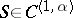 ,
, 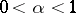 , then
, then  in
in 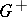 or
or 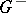 . If
. If  and
and 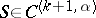 ,
, 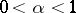 ,
, 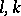 integers,
integers, 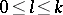 , then
, then 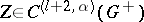 .
.
Let 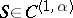 ,
, 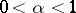 , let
, let 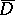 be a closed bounded domain such that
be a closed bounded domain such that 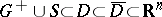 . If
. If 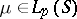 ,
, 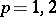 , then
, then 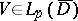 ,
, 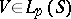 ,
, 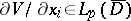 ,
, 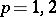 ;
; 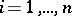 . If the density is bounded and summable, then
. If the density is bounded and summable, then
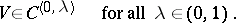 |
If 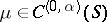 ,
, 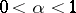 , then
, then 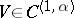 in
in 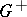 or
or 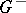 . If
. If  , then
, then 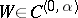 in
in 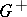 or
or 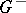 .
.
If 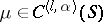 and
and 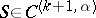 ,
, 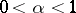 ,
, 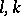 integers,
integers, 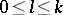 , then
, then 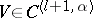 in
in 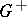 or
or 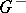 . If
. If 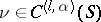 and
and 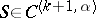 ,
, 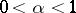 ,
,  integers,
integers, 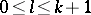 , then
, then 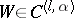 in
in 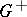 or
or  .
.
For potentials and their derivatives extended by continuity on  the above-described properties of smoothness are also valid under the corresponding smoothness conditions on the density and the surface
the above-described properties of smoothness are also valid under the corresponding smoothness conditions on the density and the surface 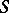 .
.
Representation of functions and solution of the principal boundary value problems in potential theory using potentials.
Let 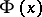 be a function of class
be a function of class  and let
and let  be a smooth surface of class
be a smooth surface of class 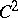 . Then the following integral identity (Green formula) holds:
. Then the following integral identity (Green formula) holds:
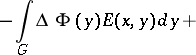 | (2) |
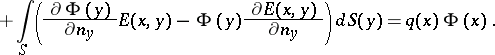 |
In particular, in 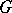 the function
the function 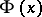 can be represented as the sum of a volume potential and single- and double-layer potentials, with respective densities
can be represented as the sum of a volume potential and single- and double-layer potentials, with respective densities
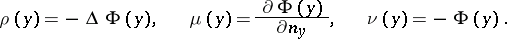 |
For a function 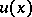 of class
of class 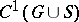 that is harmonic on
that is harmonic on 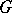 the following identity holds:
the following identity holds:
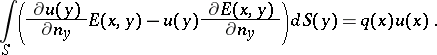 | (3) |
Hence, such a function 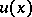 can be represented in
can be represented in 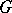 by the sum of single- and double-layer potentials with densities
by the sum of single- and double-layer potentials with densities 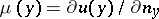 ,
, 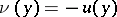 , respectively. However, the densities in (3) cannot be arbitrarily given on
, respectively. However, the densities in (3) cannot be arbitrarily given on 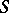 ; they are connected by the integral relation obtained from (3) for
; they are connected by the integral relation obtained from (3) for 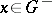 .
.
A central place in potential theory is occupied by the Dirichlet and the Neumann boundary value problem (also called the first and the second boundary value problem (cf. also Dirichlet problem; Neumann problem)) for the domains  (interior problems) and
(interior problems) and 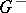 (exterior problems) which, under the assumption of sufficient smoothness, can be completely studied by reducing them to the integral equations of potential theory.
(exterior problems) which, under the assumption of sufficient smoothness, can be completely studied by reducing them to the integral equations of potential theory.
The interior Dirichlet problem: Find a function 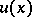 of class
of class  ,
, 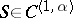 ,
, 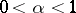 , harmonic in
, harmonic in 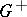 , which satisfies the boundary condition
, which satisfies the boundary condition 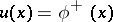 ,
, 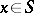 , where
, where 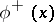 is a given continuous function on
is a given continuous function on 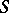 . The solution to this problem always exists, is unique and can be obtained in the form of a double-layer potential
. The solution to this problem always exists, is unique and can be obtained in the form of a double-layer potential
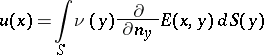 |
with density  which is obtained as the unique solution of the Fredholm integral equation of the second kind
which is obtained as the unique solution of the Fredholm integral equation of the second kind
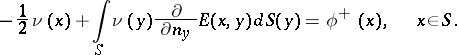 |
The interior Neumann problem: Find a function 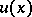 of class
of class 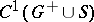 ,
, 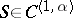 ,
, 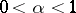 , harmonic in
, harmonic in 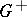 , which satisfies the boundary condition
, which satisfies the boundary condition 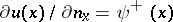 ,
, 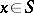 , where
, where 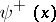 is a given continuous function on
is a given continuous function on 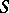 . A solution to this problem exists if and only if the function
. A solution to this problem exists if and only if the function 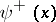 satisfies the orthogonality condition
satisfies the orthogonality condition
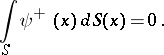 | (4) |
This solution is obtained up to an arbitrary additive constant 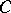 in the form
in the form 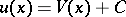 , where
, where
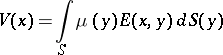 |
is a single-layer potential whose density 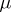 is obtained from the following Fredholm integral equation of the second kind:
is obtained from the following Fredholm integral equation of the second kind:
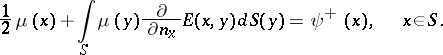 | (5) |
The continuous homogeneous equation has a non-trivial solution  and the inhomogeneous equation (5) is solvable under the condition (4); moreover, its general solution has the form
and the inhomogeneous equation (5) is solvable under the condition (4); moreover, its general solution has the form 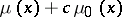 , where
, where  is an arbitrary constant.
is an arbitrary constant.
The exterior Dirichlet problem: Find a function 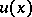 of class
of class  ,
, 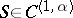 ,
, 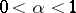 , harmonic in
, harmonic in 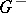 ,
, 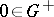 , which satisfies the boundary condition
, which satisfies the boundary condition 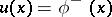 ,
, 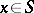 , where
, where 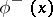 is a given continuous function on
is a given continuous function on  . Here,
. Here, 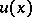 is assumed to be regular at infinity, i.e.
is assumed to be regular at infinity, i.e.
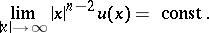 |
The solution of this problem always exists, is unique and can be obtained in the form
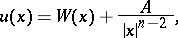 |
where 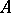 is a constant and
is a constant and
 |
is a double-layer potential whose density  is a solution of the following Fredholm integral equation of the second kind:
is a solution of the following Fredholm integral equation of the second kind:
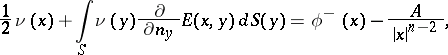 | (6) |
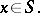 |
The corresponding homogeneous equation has the non-trivial solution 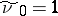 . Under an adequate choice of the constant
. Under an adequate choice of the constant 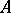 , the solution of the inhomogeneous equation (6) takes the form
, the solution of the inhomogeneous equation (6) takes the form
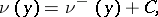 |
where 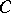 is an arbitrary constant and
is an arbitrary constant and 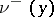 is a particular solution of (6). The constant
is a particular solution of (6). The constant 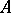 is chosen in the form
is chosen in the form
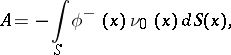 |
where the density 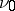 must satisfy the condition
must satisfy the condition
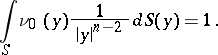 | (7) |
This density 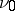 is a non-trivial solution of the equation (5) of the interior Neumann problem with data
is a non-trivial solution of the equation (5) of the interior Neumann problem with data 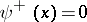 ,
, 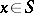 , satisfying the normalization condition
, satisfying the normalization condition
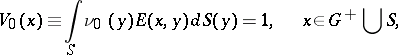 |
which is equivalent to (7) for 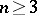 . The single-layer potential
. The single-layer potential 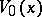 with density
with density 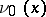 is called an equilibrium potential or Robin potential. The density
is called an equilibrium potential or Robin potential. The density 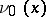 provides a solution to the Robin problem or the electrostatic problem on the distribution of charges on the conductor
provides a solution to the Robin problem or the electrostatic problem on the distribution of charges on the conductor 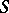 generating a constant equilibrium potential in
generating a constant equilibrium potential in  . A certain complexity in solving the exterior Dirichlet problem is due to the fact that, in general, the harmonic function
. A certain complexity in solving the exterior Dirichlet problem is due to the fact that, in general, the harmonic function 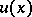 that is regular at infinity decreases slower than the double-layer potential as
that is regular at infinity decreases slower than the double-layer potential as 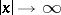 and, thus, in the general case
and, thus, in the general case 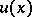 cannot be represented only by one double-layer potential.
cannot be represented only by one double-layer potential.
The exterior Neumann problem: Find a function 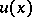 of class
of class 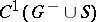 ,
, 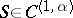 ,
, 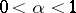 , harmonic in
, harmonic in 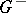 ,
, 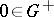 , which satisfies the boundary condition
, which satisfies the boundary condition 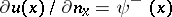 ,
, 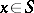 , where
, where  is a given continuous function on
is a given continuous function on 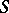 ; in addition,
; in addition, 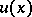 is assumed to be regular at infinity. For
is assumed to be regular at infinity. For 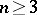 the solution of this problem always exists and is unique; for
the solution of this problem always exists and is unique; for 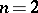 a solution exists if and only if the following condition holds:
a solution exists if and only if the following condition holds:
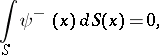 | (8) |
Moreover, this solution is defined up to an arbitrary additive constant. This solution of the exterior Neumann problem can be represented in the form of a single-layer potential
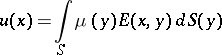 |
whose density is a solution of the following Fredholm integral equation of the second kind:
 | (9) |
For 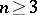 the solution of this equation always exists and is unique. For
the solution of this equation always exists and is unique. For 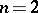 the corresponding homogeneous equation has a non-trivial solution
the corresponding homogeneous equation has a non-trivial solution 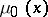 . Thus, the inhomogeneous equation (9) with the solvability condition (8) has a unique solution
. Thus, the inhomogeneous equation (9) with the solvability condition (8) has a unique solution 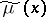 such that
such that
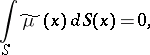 |
and its general solution is of the form 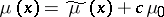 , where
, where  is an arbitrary constant.
is an arbitrary constant.
Boundary value problems in potential theory can also be solved using a Green function. For instance, for the (interior) Dirichlet problem the Green function has the form
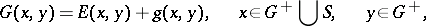 |
where 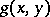 is a harmonic function in
is a harmonic function in 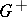 that is continuous with respect to
that is continuous with respect to  on
on 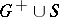 and that satisfies, for each
and that satisfies, for each 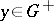 , the boundary condition
, the boundary condition 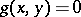 ,
, 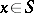 . The solution of the (interior) Dirichlet problem
. The solution of the (interior) Dirichlet problem 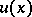 of class
of class 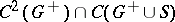 for the Poisson equation
for the Poisson equation 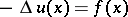 ,
, 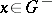 , with the boundary condition
, with the boundary condition 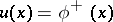 ,
, 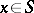 , can be represented in the form
, can be represented in the form
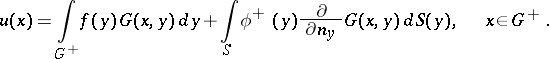 |
The integrals
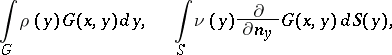 |
which depend on the parameter  , are called the Green volume potential (of the Dirichlet problem) and the Green double-layer potential, respectively. Their properties are similar to the properties of the potentials (1).
, are called the Green volume potential (of the Dirichlet problem) and the Green double-layer potential, respectively. Their properties are similar to the properties of the potentials (1).
Green functions allow one to reduce eigen value problems to integral equations. For instance, the Dirichlet problem 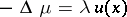 ,
, 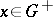 , with boundary condition
, with boundary condition 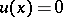 ,
, 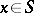 , is reduced to the following Fredholm integral equation of the second kind with a self-adjoint kernel:
, is reduced to the following Fredholm integral equation of the second kind with a self-adjoint kernel:
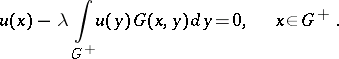 |
Further generalization of some fundamental concepts in potential theory.
Simultaneously with profound studies on the properties of the potentials (1), defined by densities of a more or less general form, and of their applications, the concept of potential itself has undergone a deep generalization related to the concepts of a Radon measure and a Radon integral. This process started in the 1920s.
Let 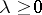 be a positive Borel measure on
be a positive Borel measure on 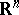 with compact support
with compact support 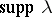 . The potential of the measure,
. The potential of the measure,
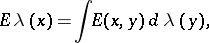 | (10) |
exists everywhere in 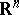 in the sense of a mapping
in the sense of a mapping 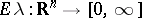 for
for 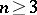 and
and 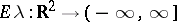 for
for  (i.e. here the value
(i.e. here the value 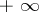 is also allowed), is a superharmonic function everywhere in
is also allowed), is a superharmonic function everywhere in 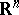 and is harmonic outside the support
and is harmonic outside the support 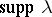 . For a measure
. For a measure  of arbitrary sign with compact support the potential
of arbitrary sign with compact support the potential 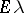 is defined on the basis of the canonical decomposition
is defined on the basis of the canonical decomposition  ,
, 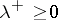 ,
, 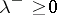 , as
, as  . At the points
. At the points  where both potentials
where both potentials 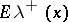 and
and  assume the value
assume the value 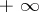 , this potential is not defined. If the measure
, this potential is not defined. If the measure 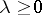 is concentrated on a smooth surface
is concentrated on a smooth surface 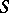 , then the double-layer potential of the measure
, then the double-layer potential of the measure 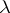 is determined similarly to (10):
is determined similarly to (10):
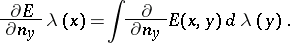 |
The potential (10) is finite, 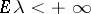 everywhere on
everywhere on 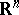 except at the points of a polar set, which is characterized as a set of outer capacity zero. If
except at the points of a polar set, which is characterized as a set of outer capacity zero. If 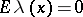 everywhere except on a set of outer capacity zero, then
everywhere except on a set of outer capacity zero, then 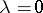 . If the measure
. If the measure 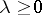 ,
,  , is concentrated on a set of capacity zero, then
, is concentrated on a set of capacity zero, then 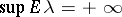 . The following maximum principle is valid:
. The following maximum principle is valid:
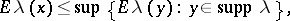 |
i.e. the least upper bound of 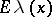 equals the least upper bound of the restriction of
equals the least upper bound of the restriction of 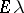 to
to 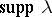 . If this restriction is continuous (in the general case, including
. If this restriction is continuous (in the general case, including 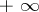 ) at a point
) at a point  , then the potential
, then the potential 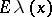 is continuous at that point
is continuous at that point 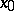 in
in 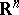 . The potentials of a measure,
. The potentials of a measure,  , can be reduced to potentials of densities (1) if and only if the measure
, can be reduced to potentials of densities (1) if and only if the measure 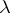 is absolutely continuous with respect to the Lebesgue measure in
is absolutely continuous with respect to the Lebesgue measure in 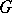 or on
or on 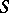 , respectively (see [3]–[6]).
, respectively (see [3]–[6]).
If 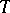 is a generalized function, or distribution, on
is a generalized function, or distribution, on 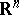 , then its potential is defined as the convolution
, then its potential is defined as the convolution 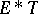 , which is also a generalized function. For instance, if
, which is also a generalized function. For instance, if 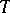 is a generalized function with compact support, then the Poisson equation
is a generalized function with compact support, then the Poisson equation 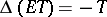 is valid on
is valid on  in the sense of the theory of generalized functions. Potentials of measures can be considered as a particular case of potentials of distributions. For potentials of distributions see [3], [4], [9].
in the sense of the theory of generalized functions. Potentials of measures can be considered as a particular case of potentials of distributions. For potentials of distributions see [3], [4], [9].
For domains 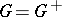 with sufficiently smooth boundary
with sufficiently smooth boundary 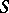 the method of potentials provides an efficient solution to the Dirichlet problem. One of the principal directions of development in potential theory consists in finding methods to prove the existence and uniqueness of a solution to the Dirichlet problem for wider classes of domains (see Balayage method; Dirichlet principle; Perron method; Schwarz alternating method). However, in 1910 S. Zaremba noted that for a plane domain
the method of potentials provides an efficient solution to the Dirichlet problem. One of the principal directions of development in potential theory consists in finding methods to prove the existence and uniqueness of a solution to the Dirichlet problem for wider classes of domains (see Balayage method; Dirichlet principle; Perron method; Schwarz alternating method). However, in 1910 S. Zaremba noted that for a plane domain 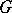 whose boundary
whose boundary 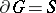 has isolated points the Dirichlet problem is not always solvable in the above classical formulation; in addition, in 1912 H. Lebesgue has shown that it is not always solvable also for spatial domains homeomorphic to a closed sphere but with a sufficiently sharp edge at the boundary entering inside the domain (a so-called Lebesgue spine, see Irregular boundary point), i.e. there exist continuous functions
has isolated points the Dirichlet problem is not always solvable in the above classical formulation; in addition, in 1912 H. Lebesgue has shown that it is not always solvable also for spatial domains homeomorphic to a closed sphere but with a sufficiently sharp edge at the boundary entering inside the domain (a so-called Lebesgue spine, see Irregular boundary point), i.e. there exist continuous functions 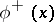 ,
, 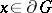 , for which the Dirichlet problem cannot be solved in any way.
, for which the Dirichlet problem cannot be solved in any way.
Thus, the generalized Perron–Wiener solution to the Dirichlet problem for the Laplace equation obtained in the course of development of the Perron method is of great importance. As has been shown by N. Wiener (1924), in this case any finite continuous function 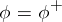 prescribed on the boundary
prescribed on the boundary 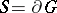 of an arbitrary bounded domain
of an arbitrary bounded domain 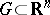 is resolutive, i.e. the generalized Perron–Wiener solution
is resolutive, i.e. the generalized Perron–Wiener solution 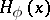 for this function exists and, moreover, is unique. In general, in 1939 M. Brelot has shown that a finite measurable function
for this function exists and, moreover, is unique. In general, in 1939 M. Brelot has shown that a finite measurable function 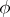 on
on 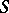 is resolutive if and only if
is resolutive if and only if  is integrable with respect to harmonic measure on
is integrable with respect to harmonic measure on  .
.
The generalized solution 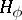 does not take the prescribed values
does not take the prescribed values 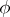 at all boundary points. A point
at all boundary points. A point 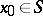 is called a regular point if for any finite continuous function
is called a regular point if for any finite continuous function 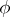 on
on 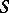 the generalized solution
the generalized solution 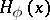 takes the value
takes the value 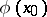 , that is,
, that is,
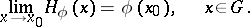 |
All other points 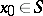 are called irregular points; they include the isolated points of the boundary when
are called irregular points; they include the isolated points of the boundary when 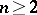 and the Lebesgue spine for
and the Lebesgue spine for 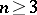 . It turned out (the Kellogg–Evans theorem, 1933) that the set of irregular points has outer capacity zero, i.e. this set is in some sense thin. The set of regular points is dense in
. It turned out (the Kellogg–Evans theorem, 1933) that the set of irregular points has outer capacity zero, i.e. this set is in some sense thin. The set of regular points is dense in 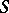 .
.
For the Dirichlet problem one can construct a generalized Green function 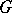 , which can be defined, e.g., for an arbitrary fixed point
, which can be defined, e.g., for an arbitrary fixed point 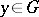 in the following way:
in the following way:
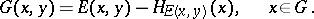 |
The generalized Green function preserves some properties of the classical Green function, for example, the symmetry property 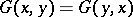 , but
, but 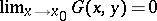 ,
, 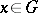 , if and only if
, if and only if 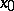 is a regular point of the boundary
is a regular point of the boundary 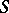 (see [4], [6]).
(see [4], [6]).
The studies of potentials with other kernels, different from 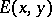 , and the study of the Dirichlet problem for compacta and the stability of the Dirichlet problem are of great importance (see [6], [4]). Their application to the solution of boundary value problems is intensively developed (see Bessel potential; Non-linear potential; Riesz potential; and also [3], [11]).
, and the study of the Dirichlet problem for compacta and the stability of the Dirichlet problem are of great importance (see [6], [4]). Their application to the solution of boundary value problems is intensively developed (see Bessel potential; Non-linear potential; Riesz potential; and also [3], [11]).
References
| [1] | N.M. [N.M. Gyunter] Günter, "Potential theory and its application to basic problems of mathematical physics" , F. Ungar (1967) (Translated from Russian) |
| [2] | L.N. Sretenskii, "Theory of the Newton potential" , Moscow-Leningrad (1946) (In Russian) |
| [3] | N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian) |
| [4] | M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959) |
| [5] | O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967) |
| [6] | M.V. Keldysh, "On the resolutivity and the stability of the Dirichlet problem" Uspekhi Mat. Nauk , 8 (1941) pp. 171–231 (In Russian) |
| [7] | A.V. Bitsadze, "Equations of mathematical physics" , MIR (1980) (Translated from Russian) |
| [8] | A.V. Bitsadze, "Boundary value problems for second-order elliptic equations" , North-Holland (1968) (Translated from Russian) |
| [9] | V.S. Vladimirov, "Equations of mathematical physics" , M. Dekker (1971) (Translated from Russian) |
| [10] | R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German) |
| [11] | C. Miranda, "Partial differential equations of elliptic type" , Springer (1970) (Translated from Italian) |
| [12] | S.G. Mikhlin, "Linear partial differential equations" , Moscow (1977) (In Russian) |
| [13] | A.N. Tikhonov, A.A. Samarskii, "Equations of mathematical physics" , Pergamon (1963) (Translated from Russian) |
Comments
See also Potential theory, mixed boundary value problems of; Potential theory, inverse problems in; Potential theory, abstract.
References
| [a1] | L.L. Helms, "Introduction to potential theory" , Wiley (Interscience) (1969) |
| [a2] | M. Tsuji, "Potential theory in modern function theory" , Chelsea, reprint (1975) |
| [a3] | J. Wermer, "Potential theory" , Lect. notes in math. , 408 , Springer (1974) |
| [a4] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 |
| [a5] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , A-B , North-Holland (1978–1982) (Translated from French) |
| [a6] | C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972) |
| [a7] | V.I. Fabrikant, "Applications of potential theory in mechanics. Selection of new results" , Kluwer (1989) |
Potential theory. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Potential_theory&oldid=48266