Potential theory, abstract

The theory of potentials on abstract topological spaces. Abstract potential theory arose in the middle of the 20th century from the efforts to create a unified axiomatic method for treating a vast diversity of properties of the different potentials that are applied to solve problems of the theory of partial differential equations. The first sufficiently complete description of the axiomatics of "harmonic" functions (i.e. solutions of an admissible class of partial differential equations) and the corresponding potentials was given by M. Brelot (1957–1958, see [1]), but it was concerned only with elliptic equations. The extension of the theory to a wide class of parabolic equations was obtained by H. Bauer (1960–1963, see [3]). The probabilistic approach to abstract potential theory, the origins of which could be found already in the works of P. Lévy, J. Doob, G. Hunt, and others, turned out to be very fruitful.

To expose abstract potential theory, the notion of a harmonic space is of great help. Let $ X $ be a locally compact topological space. A sheaf of functions on $ X $ is a mapping $ \mathfrak F $ defined on the family of all open sets of $ X $ such that

1) $ \mathfrak F ( U) $, for any open set $ U \subset X $, is a family of functions $ u : U \rightarrow \overline{\mathbf R}\; = [ - \infty , \infty ] $;

2) if two open sets $ U , V $ are such that $ U \subset V \subset X $, then the restriction of any function from $ \mathfrak F ( V) $ to $ U $ belongs to $ \mathfrak F ( U) $;

3) if for any family $ \{ U _ {i} \} $, $ i \in I $, of open sets $ U _ {i} \subset X $ the restrictions to $ U _ {i} $ of some function $ u $ defined on $ \cup _ {i \in I } U _ {i} $ belong, for any $ i \in I $, to $ \mathfrak F ( U _ {i} ) $, then $ u \in \mathfrak F ( \cup _ {i \in I } U _ {i} ) $.

A sheaf of functions $ \mathfrak H $ on $ X $ is called a harmonic sheaf if for any open set $ U \subset X $ the family $ \mathfrak H ( U) $ is a real vector space of continuous functions on $ U $. A function $ u $ defined on some set $ S \subset X $ containing the open set $ U $ is called an $ \mathfrak H $- function if the restriction $ u \mid _ {U} $ belongs to $ \mathfrak H ( U) $. A harmonic sheaf is non-degenerate at a point $ x \in X $ if in a neighbourhood of $ x $ there exists an $ \mathfrak H $- function $ u $ such that $ u ( x) \neq 0 $.

The real distinctions between the axiomatics of Bauer, Brelot and Doob can be characterized by the convergence properties of $ \mathfrak H $- functions.

a) Bauer's convergence property states that if an increasing sequence of $ \mathfrak H $- functions is locally bounded on some open set $ U \subset X $, then the limit function $ v $ is an $ \mathfrak H $- function.

b) Doob's convergence property states that if a limit function $ v $ is finite on some dense set $ U \subset X $, then $ v $ is an $ \mathfrak H $- function.

c) Brelot's convergence property states that if the limit function $ v $ of an increasing sequence of $ \mathfrak H $- functions on some domain $ U \subset X $ is finite at a point $ x \in U $, then $ v $ is an $ \mathfrak H $- function.

If the space $ X $ is locally connected, the implications c) $ \Rightarrow $ b) $ \Rightarrow $ a) hold.

A sheaf of functions $ \mathfrak U $ on $ X $ is called a hyperharmonic sheaf if for any open set $ U \subset X $ the family $ \mathfrak U ( U) $ is a convex cone of lower semi-continuous functions $ u : U \rightarrow ( - \infty , \infty ] $; a $ \mathfrak U $- function is defined in a similar way as an $ \mathfrak H $- function. The mapping $ U \rightarrow \mathfrak U ( U) \cap ( - \mathfrak U ( U) ) $ is a harmonic sheaf, denoted by $ \mathfrak H = \mathfrak H _ {\mathfrak U} $ and generated by the sheaf $ \mathfrak U $; hereafter, only this harmonic sheaf will be used.

Let on the boundary $ \partial U $ of an open set $ U \subset X $ a continuous function $ \phi : \partial U \rightarrow ( - \infty , \infty ) $ with compact support be given. The hyperharmonic sheaf $ \mathfrak U $ allows one to construct a generalized solution of the Dirichlet problem for certain open sets in the class of corresponding $ \mathfrak H $- functions by the Perron method. Let $ \overline{\mathfrak U}\; _ \phi $ be a family of lower semi-continuous $ \mathfrak U $- functions $ u $, bounded from below on $ U $, positive outside some compact set and such that

$$ \lim\limits _ {x \rightarrow y } \inf u ( x) \geq \phi ( y) ,\ \ y \in \partial U ; $$

define $ \underline{\mathfrak U} {} _ \phi $ by $ \underline{\mathfrak U} {} _ \phi = - \overline{\mathfrak U}\; _ \phi $. Now, let,

$$ \overline{H}\; _ \phi ( x) = \inf \{ {u ( x) } : { u \in \overline{\mathfrak U}\; _ \phi } \} ,\ \ x \in U , $$

and let $ \overline{H}\; _ \phi = \infty $ if $ \overline{\mathfrak U}\; _ \phi = \emptyset $. Similarly,

$$ \underline{H} {} _ \phi ( x) = \sup \{ {u ( x) } : { u \in \underline{\mathfrak U} {} _ \phi } \} ,\ \ x \in U , $$

or $ \underline{H} {} _ \phi = - \infty $. A function is called resolutive if for this function $ \overline{H}\; _ \phi $ and $ \underline{H} {} _ \phi $ coincide, $ \overline{H}\; _ \phi = \underline{H} {} _ \phi = H _ \phi $, and if $ H _ \phi $ is an $ \mathfrak H $- function; this function $ H _ \phi $ is a generalized solution of the Dirichlet problem in the class of $ \mathfrak H $- functions. An open set $ U \subset X $ is resolutive with respect to $ \mathfrak U $ if every finite continuous function with compact support on $ \partial U $ is resolutive. For a resolutive set $ U $ the mapping $ H _ \phi : C _ {c} ( \partial U ) \rightarrow \mathbf R $ is a positive linear functional, hence it determines a positive measure $ \mu _ {x} $, $ x \in U $, which is called the harmonic measure on $ \partial U $( or on $ U $) at the point $ x $( with respect to $ \mathfrak U $).

A locally compact space $ X $ with a hyperharmonic sheaf $ \mathfrak U $ turns into a harmonic space if the four corresponding axioms (see Harmonic space) hold; moreover, in the convergence axiom the property is understood in the sense of Bauer.

Often (it is like this in classical examples) one takes as a basis the harmonic sheaf $ \mathfrak H $, and the axiom of completeness serves then as a definition of a hyperharmonic sheaf. For instance, the Euclidean space $ \mathbf R ^ {n} $, $ n \geq 2 $, together with the sheaf of classical solutions of the Laplace equation or of the heat equation as $ \mathfrak H $, is a harmonic space. A harmonic space is locally connected, does not contain isolated points and has a basis consisting of connected resolutive sets (resolutive domains).

An open set $ U $ in a harmonic space $ X $ with the restriction $ \mathfrak U \mid _ {U} $ as hyperharmonic sheaf is a harmonic subspace of $ X $. A hyperharmonic function $ u $ on $ U \subset X $ is called a superharmonic function if for any relatively compact resolutive set $ V $ with $ \overline{V}\; \subset U $, the greatest minorant $ \mu ^ {V} u $ is harmonic, $ \mu ^ {V} u \in \mathfrak H ( V) $. Many properties of classical superharmonic functions (see Subharmonic function) also hold in this case. A potential is a positive superharmonic function $ u $ such that its greatest harmonic minorant on $ X $ is identically equal to zero. A harmonic space $ X $ is called a $ \mathfrak C $- harmonic (or $ \mathfrak P $- harmonic) space if for any point $ x \in X $ there exists a positive superharmonic function $ u $( a potential $ u $, respectively) on $ X $ such that $ u > 0 $. Any open set in a $ \mathfrak P $- harmonic space is resolutive.

Taking a harmonic sheaf $ \mathfrak H $ as basis and defining the corresponding hyperharmonic sheaf $ \mathfrak H ^ {*} $ by the axiom of completeness, one obtains the Bauer space, which coincides with the harmonic space for $ \mathfrak H ^ {*} $. If the harmonic sheaf $ \mathfrak H $, for any open set $ U \subset \mathbf R ^ {n} \times \mathbf R $, consists of the solutions $ h $ of the heat equation $ \Delta h - \partial h / \partial t = 0 $, then $ \mathfrak H $ has the Doob convergence property and $ \mathbf R ^ {n} \times \mathbf R $ together with this sheaf $ \mathfrak H $ is a (Bauer) $ \mathfrak P $- space. Here, $ v $ is a superharmonic function of class $ C ^ {2} $ if and only if $ \Delta v - \partial v / \partial t \leq 0 $.

A Brelot space is characterized by the following conditions: $ X $ does not have isolated points and is locally connected; the regular sets with respect to $ \mathfrak H $ form a base of $ X $( regularity means resolutivity of the classical Dirichlet problem in the class $ \mathfrak H $); and $ \mathfrak H $ has the Brelot convergence property. The Brelot spaces form a proper subclass of the so-called elliptic harmonic spaces (see [4]), i.e. the elliptic Bauer spaces. If the harmonic sheaf $ \mathfrak H $, for any open set $ U \subset \mathbf R ^ {n} $, $ n \geq 2 $, consists of the solutions $ u $ of the Laplace equation $ \Delta u = 0 $, then $ \mathbf R ^ {2} $ together with this sheaf is a Brelot $ \mathfrak C $- space, and $ \mathbf R ^ {n} $ for $ n \geq 3 $ is a Brelot $ \mathfrak P $- space. Here, $ v $ is a hyperharmonic function of class $ C ^ {2} $ if and only if $ \Delta v \leq 0 $.

A point $ y $ of the boundary $ \partial U $ of a resolutive set $ U $ is called a regular boundary point if for any finite continuous function $ \phi $ on $ \partial U $ the following limit relation holds:

$$ \lim\limits _ {x \rightarrow y } H _ \phi ( x) = \phi ( y) ,\ \ x \in U ; $$

otherwise $ y $ is called an irregular boundary point. Let $ F $ be a filter on $ U $ converging to $ y $. A strictly-positive hyperharmonic function $ v $ defined on the intersection of $ U $ with some neighbourhood of $ y $ and converging to $ 0 $ along $ F $ is called a barrier of the filter $ F $. If for a relatively compact resolutive set $ U $ in a $ \mathfrak C $- harmonic space all filters that converge to points $ y \in \partial U $ have barriers, then $ U $ is a regular set, i.e. all its boundary points are regular. If $ U $ is a relatively compact open set in a $ \mathfrak P $- harmonic space on which there exists a strictly-positive hyperharmonic function converging to $ 0 $ at each point $ y \in \partial U $, then $ U $ is a regular set.

Besides studies concerning resolutivity and regularity in the Dirichlet problem, the following problems are of major interest in abstract potential theory: the theory of capacity of point sets in harmonic spaces $ X $; the theory of balayage (see Balayage method) for functions and measures on $ X $; and the theory of integral representations of positive superharmonic functions on $ X $ generalizing the Martin representations (see Martin boundary in potential theory).

Already at the beginning of the 20th century it became evident that potential theory is closely related to certain concepts of probability theory such as Brownian motion; Wiener process; and Markov process. For instance, the probability that the trajectory of a Brownian motion in a domain $ G \subset \mathbf R ^ {2} $ starting at the point $ x _ {0} \in G $ will hit for the first time the boundary $ \partial G $ on a (Borel) set $ E \subset \partial G $ is exactly the harmonic measure of $ E $ at $ x _ {0} $; the polar sets (cf. Polar set) on $ \partial G $ are the sets that are almost-certainly not hit by the trajectory. Later on, probabilistic methods contributed to a more profound understanding of certain ideas from potential theory and led to a series of new results; on the other hand, the potential-theoretic approach led to a better understanding of the results of probability theory and also leads to new results in it.

Let $ X $ be a locally compact space with a countable base, let $ C _ {c} $ and $ C _ {0} $ be the classes of finite continuous functions on $ X $, respectively, with compact support and convergent to zero at infinity. A measure kernel $ N ( x , E ) \geq 0 $ is a (Borel) function in $ x \in X $ for every relatively compact (Borel) set $ E \subset X $. Using $ N $, to each function $ f \geq 0 $, $ f \in C _ {c} $, corresponds a potential function

$$ N f ( x) = \int\limits f ( y) N ( x , d y ) ,\ \ x \in X , $$

and to a measure $ \theta \geq 0 $ corresponds a potential measure

$$ \theta N ( E) = \int\limits N ( x , E ) d \theta ( x) . $$

The identity kernel $ I ( x , E ) $ vanishes when $ x \notin E $ and is equal to $ 1 $ when $ x \in E $, it changes neither $ f ( x) $ nor $ \theta ( E) $. For instance, in the Euclidean space $ \mathbf R ^ {3} $ the kernel

$$ N ( x , E ) = \int\limits _ { E } \frac{dy}{| x - y | } $$

determines the Newton potential $ N f $ with density $ f $, and $ \theta N $ is the measure with density equal to the density of the Newton potential of the measure $ \theta $( see Potential theory).

A product kernel has the form

$$ M N ( x , E ) = \int\limits N ( y , E ) M ( x , d y ) . $$

A family of kernels $ \{ N _ {t} \} $, $ t \geq 0 $, with the composition law $ N _ {t+} s = N _ {t} N _ {s} $ is a one-parameter semi-group. A kernel $ N $ satisfies the complete maximum principle if for any $ f , g \geq 0 $ from $ C _ {c} $ and $ a > 0 $ the inequality $ N f \leq N g + a $ on the set where $ f > 0 $ leads to this inequality everywhere on $ X $. The principal theorem in this theory is Hunt's theorem, which in its simplest version is the following: If the image of $ C _ {c} $ under a transformation $ N $ is dense in $ C _ {0} $ and if $ N $ satisfies the complete maximum principle, then there exists a semi-group $ \{ P _ {t} \} $, $ t \geq 0 $, such that

$$ N f ( x) = \int\limits _ { 0 } ^ \infty P _ {t} f ( x) d t ,\ \ f \geq 0 $$

(a Feller semi-group); moreover, $ P _ {t} $ transforms $ C _ {c} $ into $ C _ {0} $; $ P _ {0} $ is the identity kernel; $ \lim\limits _ {t \rightarrow 0 } P _ {t} f = f $, $ f \in C _ {0} $, locally uniform; and $ P _ {t} ( 1) \leq 1 $. A measurable function $ f \geq 0 $ is called an excessive function with respect to the semi-group $ \{ P _ {t} \} $ if always $ P _ {t} f \leq f $ and if $ \lim\limits _ {t \rightarrow 0 } P _ {t} f = f $; if $ P _ {t} f = f $, then $ f $ is called an invariant function. The corresponding formulas are also valid for the potential measure $ \theta N $.

The theory of Hunt (1957–1958) outlined above has a direct probabilistic sense. Let on $ X $ be given some $ \sigma $- algebra $ \mathfrak U $ of Borel sets and a probability measure $ {\mathsf P} $. A random variable $ S = S ( x) $ is a $ \mathfrak U $- measurable mapping of $ X $ into the state space $ \overline{\mathbf R}\; = [ - \infty , \infty ] $. The family of random variables $ \{ S _ {t} \} $, $ t \geq 0 $, is a Markov process (for which $ S _ {t} ( x) $ is the trajectory of a point $ x \in X $) if for any $ y $, $ - \infty \leq y < \infty $, there exists a probability measure $ {\mathsf P} ^ {y} $ on $ \mathfrak U $ such that a) $ {\mathsf P} ^ {y} ( \{ S _ {0} = y \} ) = 1 $; b) $ {\mathsf P} ^ {y} ( A) $, $ A \in \mathfrak U $, is a Borel function of $ y $; and c) the form of a trajectory passing through $ y $ at a moment $ r $, for $ t \geq r $, is independent of the positions of the points preceding it. In such Markov processes the semi-groups $ \{ {\mathsf P} _ {t} \} $ are interpreted as semi-groups of measures

$$ {\mathsf P} _ {t} ( y , B ) = {\mathsf P} ^ {y} ( \{ S _ {t} \in B \} ) . $$

Studies of excessive and invariant functions with respect to the semi-groups $ \{ {\mathsf P} _ {t} \} $ are of great importance.

On the other hand, if $ X $ is a $ \mathfrak P $- harmonic space with a countable base, then one can always choose on it a potential kernel to meet the requirements of Hunt's theorem; in this case the excessive functions of the associated semi-group are precisely the non-negative hyperharmonic functions. Hunt's theorem can be also generalized for some types of Bauer spaces (see [4], [7]).

Other concepts from abstract potential theory, such as, for example, balayage, polar and thin sets, also have their probabilistic interpretation within the framework of the general theory of random processes; this facilitates studies of the latter. On the other hand, the potential-theoretic approach to a series of concepts, such as, for example, martingales, which are beyond the limits of Markov processes, turned out to be of great importance.

References

[1]	M. Brélot, "Lectures on potential theory" , Tata Inst. (1960)
[2]	M. Brelot, "Les étapes et les aspects multiples de la théorie du potentiel" Enseign. Math. , 18 : 1 (1972) pp. 1–36
[3]	H. Bauer, "Harmonische Räume und ihre Potentialtheorie" , Springer (1966)
[4]	C. Constantinescu, A. Cornea, "Potential theory on harmonic spaces" , Springer (1972)
[5]	P.A. Meyer, "Probability and potentials" , Blaisdell (1966)
[6a]	G.A. Hunt, "Markov processes and potentials, I" Illinois J. Math. , 1 (1957) pp. 44–93
[6b]	G.A. Hunt, "Markov processes and potentials, II" Illinois J. Math. , 1 (1957) pp. 316–362
[6c]	G.A. Hunt, "Markov processes and potentials, III" Illinois J. Math. , 2 (1958) pp. 151–213
[7]	R.M. Blumenthal, R.K. Getoor, "Markov processes and potential theory" , Acad. Press (1968)

Comments

Abstract potential theory is also called axiomatic potential theory.

A measure kernel $ N( x, E) $ is also defined as a ( $ \sigma $- additive, non-negative) measure in $ E $, and $ Nf: x \rightarrow Nf( x) $ can be defined whenever $ f $ is Borel and non-negative; in the article above, $ Nf $ is assumed finite if $ f \in C _ {c} $. By definition, a Feller semi-group $ ( P _ {t} ) $ transforms $ C _ {0} $ to $ C _ {0} $, $ P _ {0} $ is the identity kernel and for $ f \in C _ {0} $ the transformation $ t \rightarrow P _ {t} f $ is continuous at 0 for the uniform topology. If $ N $ and $ ( P _ {t} ) $ are related by Hunt's theorem, $ N $ is called the potential kernel of the Feller semi-group $ ( P _ {t} ) $, and for any non-negative Borel function $ f $ the potential $ Nf $ of $ f $ is an excessive function with respect to the semi-group $ ( P _ {t} ) $. One can define analogously excessive measures and potential measures, and their study is also of great importance. The passage in the article on the definition of a Markov process is somewhat misleading: the $ X $ equipped with the $ \sigma $- algebra $ \mathfrak U $ has to be replaced by an extraneous measurable space, say $ ( \Omega , \mathfrak U ) $, and the state space $ \overline{\mathbf R}\; $ by the locally compact space $ X $ where the Hunt kernel $ N $ is defined, so that in the equality $ {\mathsf P} _ {t} ( y, B) = {\mathsf P} ^ {y} ( S _ {t} \in B ) $ one has $ y \in X $ and $ B \subseteq X $( and Borel). See Markov process.

Around 1959, A. Beurling and J. Deny introduced another branch of abstract potential theory: the notion of Dirichlet space, an axiomatization of the theory of the Dirichlet integral. See [a3].

Several abstract theories have been introduced, aimed at a unification of different branches of potential theory, e.g. the theory of balayage spaces, cf. [a2], and the theory of $ H $- cones, cf. [a1]. Both concepts use a convex cone of functions (the positive hyperharmonic functions, e.g.), satisfying some convergence properties, a Riesz property and a separation property as their main tool. See also [a4] for short surveys.

References

[a1]	N. Boboc, Gh. Bucur, A. Cornea, "Order and convexity in potential theory: 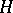-cones" , Springer (1981)
[a2]	J. Bliedtner, W. Hansen, "Potential theory. An analytic and probabilistic approach to balayage" , Springer (1986)
[a3]	M. Fukushima, "Dirichlet forms and Markov processes" , North-Holland (1980)
[a4]	J. Král (ed.) J. Lukeš (ed.) J. Veselý (ed.) , Potential theory. Survey and problems (Prague, 1987) , Lect. notes in math. , 1344 , Springer (1988)
[a5]	M. Brelot (ed.) H. Bauer (ed.) J.-M. Bony (ed.) J. Deny (ed.) G. Mokobodzki (ed.) , Potential theory (CIME, Stresa, 1969) , Cremonese (1970)
[a6]	C. Dellacherie, P.A. Meyer, "Probabilities and potential" , C , North-Holland (1988) (Translated from French)
[a7]	F.Y. Maeda, "Dirichlet integrals on harmonic spaces" , Lect. notes in math. , 803 , Springer (1980)
[a8]	M. Röckner, "Markov property of generalized fields and axiomatic potential theory" Math. Ann. , 264 (1983) pp. 153–177