Schwarz alternating method
One of the general methods for finding a solution to the Dirichlet problem; it allows one to obtain a solution to the Dirichlet problem for a differential equation of elliptic type in domains $ D $
that can be represented as the union of a finite number of domains $ D _ {j} $
in which the solution to the Dirichlet problem is already known. Studies of H.A. Schwarz (1869; see [1]) and a number of later studies by other authors were dedicated to this method for finding a solution to the Dirichlet problem for the Laplace equation in plane domains. The principal idea of the Schwarz alternating method as applied to the simplest case of the Laplace equation in the union of two plane domains is the following.
Let $ A $ and $ B $ be two domains in the plane with non-empty intersection and such that the solution to the Dirichlet problem for the Laplace equation is known for each of them. For instance, if $ A $ and $ B $ are discs, then the solution to the Dirichlet problem for each of them is given by the Poisson integral. Further, let $ D $ be the union of $ A $ and $ B $ for which a solution to the Dirichlet problem is sought (see Fig.). Let $ \alpha $ denote the boundary of $ A $, let $ \alpha _ {1} $ denote the parts of $ \alpha $ that are in $ B $( they are interior in $ D $) and let $ \alpha _ {2} $ be the remaining parts, so that $ \alpha = \alpha _ {1} \cup \alpha _ {2} $. Similarly, $ \beta $ is the boundary of $ B $, $ \beta _ {1} $ are its parts that fall in $ A $( they are also interior in $ D $) and $ \beta _ {2} $ are the remaining parts, that is, $ \beta = \beta _ {1} \cup \beta _ {2} $. Then the boundary $ \gamma $ of $ D $ can be represented in the form $ \gamma = \alpha _ {2} \cup \beta _ {2} $.
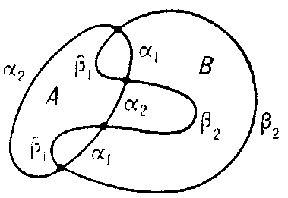
Figure: s083490a
Now, given a continuous function $ f $ on $ \gamma $, one has to find a harmonic function $ w $ in $ D $ that is continuous in the closed domain $ \overline{D}\; $ and that takes on $ \gamma $ the values of $ f $. The restriction of $ f $ to $ \alpha _ {2} $ can be continuously extended to the whole boundary $ \alpha $, and for these boundary values one finds a solution $ u _ {1} $ to the Dirichlet problem in $ A $. The values of $ u _ {1} $ on $ \beta _ {1} $ together with the values of $ f $ on $ \beta _ {2} $ now form a continuous function on $ \beta $ for which a solution $ v _ {1} $ to the Dirichlet problem in $ B $ is found. Further, a solution $ u _ {2} $ to the Dirichlet problem in $ A $ is constructed, based on the values of $ f $ on $ \alpha _ {2} $ and $ v _ {1} $ on $ \alpha _ {1} $, etc. The sought function has the form
$$ w = \lim\limits _ {n \rightarrow \infty } u _ {n} \ \mathop{\rm in} A $$
and
$$ w = \lim\limits _ {n \rightarrow \infty } v _ {n} \ \mathop{\rm in} B. $$
Using bounded solutions of the Dirichlet problem with piecewise-continuous boundary data allows one to choose the values zero on the remaining parts of the boundaries without having to worry about the continuous extension of $ f $.
A method analogous to the Schwarz alternating method (see [2]) can be applied to finding a solution to the Dirichlet problem in the intersection of two domains $ A $ and $ B $, if its solutions for $ A $ and $ B $ are known.
Schwarz' alternating method is also used to solve boundary value problems of a more general nature for general equations of elliptic type (including equations of an order greater than two) under certain additional conditions [3], and also in domains in space.
Schwarz' alternating method is extremely important for the construction of various harmonic functions (with pre-assigned singularities) on Riemann surfaces [4].
References
| [1] | H.A. Schwarz, "Gesamm. math. Abhandl." , 2 , Springer (1890) |
| [2] | C. Neumann, Ber. Verh. Sächs. Akad. Wiss. Leipzig Math.-Nat. Kl. , 22 (1870) pp. 264–321 |
| [3] | L.V. Kantorovich, V.I. Krylov, "Approximate methods of higher analysis" , Noordhoff (1958) (Translated from Russian) MR0106537 Zbl 0083.35301 |
| [4] | R. Nevanlinna, "Uniformisierung" , Springer (1967) MR0228671 Zbl 0152.27401 |
Comments
Recently these ideas are meeting new interest among numerical analysts. They are essentially used to solve boundary value problems on complicated domains. Such domains are decomposed in smaller and simpler ones; therefore such methods are referred to as domain decomposition methods.
See [a1], pp. 200-203, for a more subtle application of the Schwarz alternating method in the study of boundary value problems.
References
| [a1] | L.L. Helms, "Introduction to potential theory" , Wiley (Interscience) (1969) |
| [a2] | T.F. Chan, et al., "Domain decomposition methods for partial differential equations" , SIAM (1990) MR1064333 Zbl 0695.00026 |
Schwarz alternating method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Schwarz_alternating_method&oldid=48628