Difference between revisions of "Hopf order"
(→References: Underwood (2011)) |
m (isbn) |
||
| Line 1: | Line 1: | ||
| − | Let | + | Let $K$ be a finite extension of the $p$-adic rationals <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h1102803.png" /> endowed with the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h1102804.png" />-adic valuation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h1102805.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h1102806.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h1102807.png" /> be its ring of integers (cf. [[Extension of a field|Extension of a field]]; [[Norm on a field|Norm on a field]]; [[P-adic number|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h1102808.png" />-adic number]]). Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h1102809.png" /> be the group ring of a [[Finite group|finite group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028010.png" /> (cf. also [[Group algebra|Group algebra]]; [[Cross product|Cross product]]), with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028011.png" />. An <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028013.png" />-Hopf order in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028014.png" /> is a rank-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028015.png" /> <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028016.png" />-Hopf algebra <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028017.png" /> (cf. [[Hopf algebra|Hopf algebra]]) satisfying <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028018.png" /> as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028019.png" />-Hopf algebras. |
There is a method [[#References|[a2]]] for constructing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028020.png" />-Hopf orders in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028021.png" /> using so-called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028022.png" />-adic order-bounded group valuations on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028023.png" />. Given a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028024.png" />-adic order-bounded group valuation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028025.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028026.png" /> be an element in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028027.png" /> of value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028028.png" />. Then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028029.png" />-Hopf order in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028030.png" /> determined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028031.png" /> (called a Larson order) is of the form | There is a method [[#References|[a2]]] for constructing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028020.png" />-Hopf orders in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028021.png" /> using so-called <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028022.png" />-adic order-bounded group valuations on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028023.png" />. Given a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028024.png" />-adic order-bounded group valuation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028025.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028026.png" /> be an element in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028027.png" /> of value <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028028.png" />. Then the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028029.png" />-Hopf order in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028030.png" /> determined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/h/h110/h110280/h11028031.png" /> (called a Larson order) is of the form | ||
| Line 47: | Line 47: | ||
<TR><TD valign="top">[a5]</TD> <TD valign="top"> R.G. Underwood, "The valuative condition and $R$-Hopf algebra orders in $KC_{p^3}$" ''Amer. J. Math. (4)'' , '''118''' (1996) pp. 701–743 {{ZBL|0857.16039}}</TD></TR> | <TR><TD valign="top">[a5]</TD> <TD valign="top"> R.G. Underwood, "The valuative condition and $R$-Hopf algebra orders in $KC_{p^3}$" ''Amer. J. Math. (4)'' , '''118''' (1996) pp. 701–743 {{ZBL|0857.16039}}</TD></TR> | ||
| − | <TR><TD valign="top">[b1]</TD> <TD valign="top"> R.G. Underwood, "An Introduction to Hopf Algebras" Springer (2011) ISBN 978-0-387-72765-3 {{ZBL|1234.16022}}</TD></TR> | + | <TR><TD valign="top">[b1]</TD> <TD valign="top"> R.G. Underwood, "An Introduction to Hopf Algebras" Springer (2011) {{ISBN|978-0-387-72765-3}} {{ZBL|1234.16022}}</TD></TR> |
</table> | </table> | ||
| + | |||
| + | {{TEX|want}} | ||
Revision as of 08:51, 12 November 2023
Let $K$ be a finite extension of the $p$-adic rationals 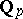 endowed with the
endowed with the 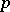 -adic valuation
-adic valuation  with
with 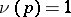 and let
and let 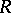 be its ring of integers (cf. Extension of a field; Norm on a field;
be its ring of integers (cf. Extension of a field; Norm on a field;  -adic number). Let
-adic number). Let 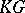 be the group ring of a finite group
be the group ring of a finite group 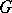 (cf. also Group algebra; Cross product), with
(cf. also Group algebra; Cross product), with 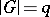 . An
. An 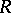 -Hopf order in
-Hopf order in 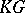 is a rank-
is a rank-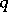
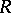 -Hopf algebra
-Hopf algebra 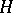 (cf. Hopf algebra) satisfying
(cf. Hopf algebra) satisfying  as
as 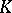 -Hopf algebras.
-Hopf algebras.
There is a method [a2] for constructing 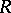 -Hopf orders in
-Hopf orders in 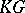 using so-called
using so-called 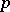 -adic order-bounded group valuations on
-adic order-bounded group valuations on 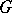 . Given a
. Given a 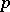 -adic order-bounded group valuation
-adic order-bounded group valuation 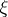 , let
, let 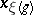 be an element in
be an element in 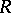 of value
of value 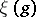 . Then the
. Then the 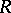 -Hopf order in
-Hopf order in 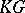 determined by
determined by 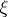 (called a Larson order) is of the form
(called a Larson order) is of the form
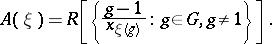 |
For 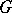 Abelian (cf. Abelian group), the classification of
Abelian (cf. Abelian group), the classification of 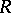 -Hopf orders in
-Hopf orders in 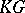 is reduced to the case where
is reduced to the case where 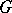 is a
is a 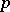 -group. Specifically, one takes
-group. Specifically, one takes 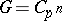 ,
, 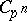 cyclic of order
cyclic of order 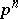 , and assumes that
, and assumes that 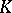 contains a primitive
contains a primitive  th root of unity, denoted by
th root of unity, denoted by 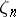 . In this case, a
. In this case, a 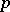 -adic order-bounded group valuation
-adic order-bounded group valuation 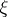 on
on 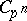 is determined by its values
is determined by its values 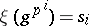 for
for 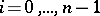 ,
, 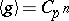 , and the Larson order
, and the Larson order 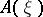 is denoted by
is denoted by
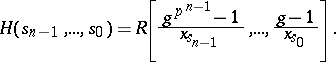 |
It is known [a3] that every 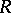 -Hopf order
-Hopf order 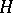 in
in  can be written as a Tate–Oort algebra
can be written as a Tate–Oort algebra 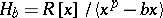 , which in turn can be expressed as the Larson order
, which in turn can be expressed as the Larson order
 |
Thus, every  -Hopf order in
-Hopf order in 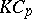 is Larson. For
is Larson. For 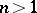 this is not the case, though every
this is not the case, though every 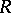 -Hopf order does contain a maximal Larson order [a2].
-Hopf order does contain a maximal Larson order [a2].
For 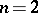 there exists a large class of
there exists a large class of 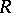 -Hopf orders in
-Hopf orders in 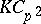 (called Greither orders), of the form
(called Greither orders), of the form
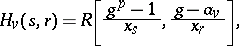 |
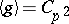 , where
, where  and
and  are values from a
are values from a 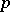 -adic order-bounded group valuation on
-adic order-bounded group valuation on 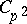 and
and 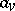 is an element in the Larson order
is an element in the Larson order 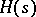 (see [a1]). The parameter
(see [a1]). The parameter  is an element in the units group
is an element in the units group  , where
, where  is the ramification index of
is the ramification index of 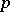 in
in 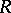 , and
, and 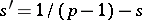 . If
. If 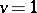 , then the Greither order
, then the Greither order 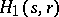 is the Larson order
is the Larson order 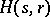 ; moreover,
; moreover,  if and only if
if and only if 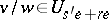 .
.
Since 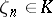 , the linear dual
, the linear dual 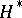 of the
of the 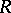 -Hopf order
-Hopf order 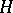 in
in 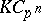 is an
is an 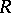 -Hopf order in
-Hopf order in 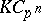 . One has
. One has
 |
and
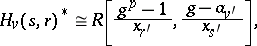 |
where 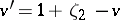 ,
, 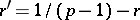 (see [a5]). It is known [a4] that an arbitrary
(see [a5]). It is known [a4] that an arbitrary 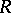 -Hopf order in
-Hopf order in 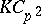 is either a Greither order or the linear dual of a Greither order. Thus, every
is either a Greither order or the linear dual of a Greither order. Thus, every 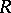 -Hopf order in
-Hopf order in 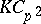 can be written in the form
can be written in the form
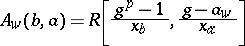 |
for some  ,
, 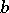 ,
, 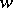 .
.
The construction of Greither orders can be generalized to give a complete classification of 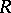 -Hopf orders in
-Hopf orders in 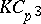 , as well as a class of
, as well as a class of 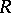 -Hopf orders in
-Hopf orders in 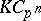 ,
, 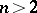 , which are not Larson (see [a5]). However, the complete classification of
, which are not Larson (see [a5]). However, the complete classification of 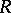 -Hopf orders in
-Hopf orders in 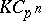 ,
, 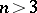 , remains an open problem.
, remains an open problem.
See also Hopf orders, applications of.
References
| [a1] | C. Greither, "Extensions of finite group schemes, and Hopf Galois theory over a complete discrete valuation ring" Math. Z. , 210 (1992) pp. 37–67 Zbl 0737.11038 |
| [a2] | R.G. Larson, "Hopf algebra orders determined by group valuations" J. Algebra , 38 (1976) pp. 414–452 Zbl 0407.20007 |
| [a3] | J. Tate, F. Oort, "Group schemes of prime order" Ann. Sci. Ecole Norm. Super. (4) , 3 (1970) |
| [a4] | R.G. Underwood, "$R$-Hopf algebra orders in $KC_{p^2}$" J. Algebra , 169 (1994},) pp. 418–440 Zbl 0820.16036 |
| [a5] | R.G. Underwood, "The valuative condition and $R$-Hopf algebra orders in $KC_{p^3}$" Amer. J. Math. (4) , 118 (1996) pp. 701–743 Zbl 0857.16039 |
| [b1] | R.G. Underwood, "An Introduction to Hopf Algebras" Springer (2011) ISBN 978-0-387-72765-3 Zbl 1234.16022 |
Hopf order. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hopf_order&oldid=42726