Difference between revisions of "Vector bundle"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
Ulf Rehmann (talk | contribs) m (tex encoded by computer) |
||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | v0963801.png | ||
| + | $#A+1 = 143 n = 1 | ||
| + | $#C+1 = 143 : ~/encyclopedia/old_files/data/V096/V.0906380 Vector bundle | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | A | + | A [[Fibre space|fibre space]] $ \pi : X \rightarrow B $ |
| + | each fibre $ \pi ^ {-} 1 ( b) $ | ||
| + | of which is endowed with the structure of a (finite-dimensional) [[Vector space|vector space]] $ V $ | ||
| + | over a skew-field $ {\mathcal P} $ | ||
| + | such that the following local triviality condition is satisfied. Each point $ b \in B $ | ||
| + | has an open neighbourhood $ U $ | ||
| + | and an $ U $- | ||
| + | isomorphism of fibre bundles $ \phi : \pi ^ {-} 1 ( U) \rightarrow U \times V $ | ||
| + | such that $ \phi \mid _ {\pi ^ {-} 1 ( b) } : \pi ^ {-} 1 ( b) \rightarrow b \times V $ | ||
| + | is an isomorphism of vector spaces for each $ b \in B $; | ||
| + | $ \mathop{\rm dim} V $ | ||
| + | is said to be the dimension of the vector bundle. The sections of a vector bundle $ \pi $ | ||
| + | form a locally free module $ \Gamma ( \pi ) $ | ||
| + | over the ring of continuous functions on $ B $ | ||
| + | with values in $ {\mathcal P} $. | ||
| + | A morphism of vector bundles is a morphism of fibre bundles $ f: \pi \rightarrow \pi ^ \prime $ | ||
| + | for which the restriction to each fibre is linear. The set of vector bundles and their morphisms forms the category $ \mathbf{Bund} $. | ||
| + | The concept of a vector bundle arose as an extension of the [[Tangent bundle|tangent bundle]] and the [[Normal bundle|normal bundle]] in differential geometry; by now it has become a basic tool for studies in various branches of mathematics: differential and algebraic topology, the theory of linear connections, algebraic geometry, the theory of (pseudo-) differential operators, etc. | ||
| − | + | A subset $ X ^ \prime \subset X $ | |
| + | such that $ \pi \mid _ {X} ^ \prime : X ^ \prime \rightarrow B $ | ||
| + | is a vector bundle and $ X ^ \prime \cap \pi ^ {-} 1 ( b) $ | ||
| + | is a vector subspace in $ \pi ^ {-} 1 ( b) $ | ||
| + | is said to be a subbundle of the vector bundle $ \pi $. | ||
| + | For instance, let $ V $ | ||
| + | be a vector space and let $ G _ {k} ( V) $ | ||
| + | be the [[Grassmann manifold|Grassmann manifold]] of subspaces of $ V $ | ||
| + | of dimension $ k $; | ||
| + | the subspace of the product $ G _ {k} ( V) \times V $, | ||
| + | consisting of pairs $ ( p, v) $ | ||
| + | such that $ v \in p $, | ||
| + | will then be a subbundle $ \gamma _ {k} $ | ||
| + | of the trivial vector bundle $ G _ {k} ( V) \times V $. | ||
| + | The union of all vector spaces $ \pi ^ {-} 1 ( b) / \pi _ {2} ^ {-} 1 ( b) $, | ||
| + | where $ \pi _ {2} $ | ||
| + | is a subbundle of $ \pi $ | ||
| + | endowed with the quotient topology, is said to be a quotient bundle of $ \pi $. | ||
| + | Let, furthermore, $ V $ | ||
| + | be a vector space and let $ G ^ {k} ( V) $ | ||
| + | be the Grassmann manifold of subspaces of $ V $ | ||
| + | of codimension $ k $; | ||
| + | the quotient bundle $ \gamma ^ {k} $ | ||
| + | of the trivial vector bundle $ G ^ {k} ( V) \times V $ | ||
| + | is defined as the quotient space of the product $ G ^ {k} ( V) \times V $ | ||
| + | by the subbundle consisting of all pairs $ ( p, v) $, | ||
| + | $ v \in p $. | ||
| + | The concepts of a subbundle and a quotient bundle are used in contraction and glueing operations used to construct vector bundles over quotient spaces. | ||
| + | |||
| + | A $ B $- | ||
| + | morphism of vector bundles $ f : \pi \rightarrow \pi ^ \prime $ | ||
| + | is said to be of constant rank (pure) if $ \mathop{\rm dim} \mathop{\rm ker} f \ \mid _ {\pi ^ {-} 1 ( b) } $ | ||
| + | is locally constant on $ B $. | ||
| + | Injective and surjective morphisms are exact and are said to be monomorphisms and epimorphisms of the vector bundle, respectively. The following vector bundles are uniquely defined for a morphism $ f $ | ||
| + | of locally constant rank: $ \mathop{\rm Ker} f $( | ||
| + | the kernel of $ f $), | ||
| + | which is a subbundle of $ \pi $; | ||
| + | $ \mathop{\rm Im} f $( | ||
| + | the image of $ f $), | ||
| + | which is a subbundle of $ \pi ^ \prime $; | ||
| + | $ \mathop{\rm Coker} f $( | ||
| + | the cokernel of $ f $), | ||
| + | which is a quotient bundle of $ \pi $; | ||
| + | and $ \mathop{\rm Coim} f $( | ||
| + | the co-image of $ f $), | ||
| + | which is a quotient bundle of $ \pi ^ \prime $. | ||
| + | Any subbundle $ \pi _ {1} $ | ||
| + | is the image of some monomorphism $ i: \pi _ {1} \rightarrow \pi $, | ||
| + | while any quotient bundle $ \pi _ {2} $ | ||
| + | is the cokernel of some epimorphism $ j : \pi \rightarrow \pi _ {2} $. | ||
| + | A sequence of $ B $- | ||
| + | morphisms of vector bundles | ||
| + | |||
| + | $$ | ||
| + | {} \dots \rightarrow \pi ^ \prime \rightarrow \pi \rightarrow \pi ^ {\prime\prime} \rightarrow \dots | ||
| + | $$ | ||
is said to be exact if the sequence | is said to be exact if the sequence | ||
| − | + | $$ | |
| + | {} \dots \rightarrow ( \pi ^ \prime ) ^ {-} 1 ( b) \rightarrow \pi ^ {-} 1 ( b) | ||
| + | \rightarrow ( \pi ^ {\prime\prime} ) ^ {-} 1 ( b) \rightarrow \dots | ||
| + | $$ | ||
| − | is exact for all | + | is exact for all $ b \in B $. |
| + | In particular, the sequence | ||
| − | + | $$ | |
| + | 0 \rightarrow \pi _ {1} \rightarrow ^ { i } \pi \rightarrow ^ { j } \pi _ {2} \rightarrow 0 , | ||
| + | $$ | ||
| − | where | + | where $ 0 $ |
| + | is the zero vector bundle, is exact if $ i $ | ||
| + | is a monomorphism, $ j $ | ||
| + | is an epimorphism and $ \mathop{\rm Im} i = { \mathop{\rm Ker} } j $. | ||
| + | The set of vector bundles over $ B $ | ||
| + | and $ B $- | ||
| + | morphisms of locally constant rank forms an exact subcategory $ \mathbf{Bund} _ {B} $ | ||
| + | of the category $ \mathbf{Bund} $. | ||
| − | For any vector bundle | + | For any vector bundle $ \pi : X \rightarrow B $ |
| + | and mapping $ u: B _ {1} \rightarrow B $, | ||
| + | the [[Induced fibre bundle|induced fibre bundle]] $ u ^ {*} ( \pi ) $ | ||
| + | is endowed with a vector bundle structure such that the morphism $ U: u ^ {*} ( \pi ) \rightarrow \pi $ | ||
| + | is a vector bundle morphism. This structure is unique and has the following property: Every fibre mapping $ {( u ^ {*} ( \pi )) } ^ {-} 1 ( b) \rightarrow \pi ^ {-} 1 ( u( b)) $ | ||
| + | is an isomorphism of vector spaces. For instance, a vector bundle of dimension $ k $ | ||
| + | over a paracompact space $ B $ | ||
| + | is isomorphic to one of the vector bundles $ u ^ {*} ( \gamma _ {k} ) $ | ||
| + | and $ \widetilde{u} {} ^ {*} ( \gamma ^ {k} ) $ | ||
| + | induced by certain mappings $ u: B \rightarrow G _ {k} ( V) $ | ||
| + | and $ \widetilde{u} : B \rightarrow G ^ {k} ( V) $, | ||
| + | respectively; moreover, homotopic mappings induce isomorphic vector bundles and, if $ \mathop{\rm dim} V \neq \infty $, | ||
| + | the converse is true: To isomorphic vector bundles there correspond homotopic mappings $ u $ | ||
| + | and $ \widetilde{u} $. | ||
| + | This is one of the fundamental theorems in the homotopic classification of vector bundles, expressing the universal character of the vector bundles $ \gamma _ {k} $ | ||
| + | and $ \gamma ^ {k} $ | ||
| + | with respect to the classifying mappings $ u $ | ||
| + | and $ \widetilde{u} $. | ||
| − | Any continuous operation ([[Functor|functor]]) | + | Any continuous operation ([[Functor|functor]]) $ T $ |
| + | on the category of vector spaces uniquely determines a continuous functor on the category of vector bundles over $ B $; | ||
| + | in this way it is possible to construct bundles associated with a given vector bundle: tensor bundles, vector bundles of morphisms $ { \mathop{\rm Hom} } _ {B} ( \pi , \pi ^ \prime ) $ | ||
| + | and, in particular, the dual vector bundle $ \pi ^ {*} $, | ||
| + | exterior powers of vector bundles, etc., whose sections are vector bundles with supplementary structures. These are extensively employed in practical applications. | ||
| − | A direct sum (Whitney sum) | + | A direct sum (Whitney sum) $ \pi \oplus \pi ^ \prime $ |
| + | and tensor product $ \pi \otimes \pi ^ \prime $ | ||
| + | have been defined for two vector bundles $ \pi $ | ||
| + | and $ \pi ^ \prime $. | ||
| + | With respect to these operations the set of classes $ { \mathop{\rm Vekt} } _ {B} $ | ||
| + | of isomorphic vector bundles over $ B $ | ||
| + | forms a semi-ring which plays an important part in the construction of a [[K-functor| $ K $- | ||
| + | functor]]; thus, if for vector bundles $ \pi $ | ||
| + | and $ \pi ^ \prime $ | ||
| + | there exist trivial vector bundles $ \theta $ | ||
| + | and $ \theta ^ \prime $ | ||
| + | such that the vector bundles $ \pi \oplus \theta $ | ||
| + | and $ \pi ^ \prime \oplus \theta ^ \prime $ | ||
| + | are isomorphic (i.e. $ \pi $ | ||
| + | and $ \pi ^ \prime $ | ||
| + | are stably equivalent), then their images in the "completion" $ K ( B) $ | ||
| + | of the semi-ring $ { \mathop{\rm Vekt} } _ {B} $ | ||
| + | are identical; moreover, the fact that the ring $ K( B) $ | ||
| + | and the set of classes of stably-equivalent vector bundles coincide follows from the existence of an inverse vector bundle for any vector bundle over a paracompact space. | ||
| − | For any vector bundle | + | For any vector bundle $ \pi : X \rightarrow B $ |
| + | over a paracompact space $ B $ | ||
| + | there exists a section $ \beta $ | ||
| + | of the vector bundle | ||
| − | + | $$ | |
| + | \pi ^ {*} \oplus \pi ^ {*} = \mathop{\rm Hom} ( \pi \oplus \pi , P ), | ||
| + | $$ | ||
| − | where | + | where $ P $ |
| + | is a trivial one-dimensional vector bundle, which on each fibre $ \pi ^ {-} 1 ( b) $ | ||
| + | is a positive-definite form, i.e. $ \pi $ | ||
| + | is metrizable; this makes it possible to establish, in particular, the splittability of an arbitrary exact sequence of vector bundles | ||
| − | + | $$ | |
| + | 0 \rightarrow \xi \rightarrow ^ { u } \pi \rightarrow ^ { v } \zeta \rightarrow 0 | ||
| + | $$ | ||
| − | in which | + | in which $ \pi $ |
| + | is metrizable, that is, the existence of a morphism $ w : \xi \oplus \zeta \rightarrow \pi $ | ||
| + | such that $ wi = u $, | ||
| + | $ vw = j $, | ||
| + | where $ i $ | ||
| + | is the imbedding into the first term and $ j $ | ||
| + | is the projection onto the second term. | ||
| − | If, in each fibre | + | If, in each fibre $ \pi ^ {-} 1 ( b) $ |
| + | of the vector bundle $ \pi : X \rightarrow B $, | ||
| + | one identifies the points lying on the same line passing through zero, one obtains a bundle $ \pi _ {0} : \Pi _ {( \pi ) } \rightarrow B $, | ||
| + | which is associated with $ \pi $ | ||
| + | and is said to be its projectivization; a fibre of $ \pi _ {0} $ | ||
| + | is the projective space $ \Pi ( V) $ | ||
| + | which is associated with $ V $. | ||
| + | This bundle is used to study Thom spaces $ T ( \pi ) = \Pi ( \pi \oplus P)/ \Pi ( \pi ) $( | ||
| + | cf. [[Thom space|Thom space]]), used in the homotopic interpretation of classes of bordant manifolds, characteristic classes of vector bundles describing the homological properties of manifolds, etc. | ||
| − | The concept of a vector bundle can be generalized to the case when the fibre is an infinite-dimensional vector space; in doing so, one must distinguish between the different topologies of the space of morphisms | + | The concept of a vector bundle can be generalized to the case when the fibre is an infinite-dimensional vector space; in doing so, one must distinguish between the different topologies of the space of morphisms $ { \mathop{\rm Hom} } ( \pi , \pi ^ \prime ) $, |
| + | suitably modify the definitions of a pure morphism and an exact sequence of morphisms, and also the construction of vector bundles associated with continuous functors on the category of infinite-dimensional vector spaces. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[1]</TD> <TD valign="top"> C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) {{MR|0242081}} {{ZBL|0653.53001}} {{ZBL|0284.53018}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380142.png" />-theory: lectures" , Benjamin (1967) {{MR|224083}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III {{MR|1931083}} {{MR|1532744}} {{MR|0155257}} {{ZBL|1008.57001}} {{ZBL|0103.15101}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) {{MR|0229247}} {{ZBL|0144.44804}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) {{MR|0533884}} {{ZBL|0444.32004}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) {{MR|1335917}} {{MR|0202713}} {{ZBL|0376.14001}} </TD></TR></table> | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) {{MR|0242081}} {{ZBL|0653.53001}} {{ZBL|0284.53018}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M.F. Atiyah, "<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096380/v096380142.png" />-theory: lectures" , Benjamin (1967) {{MR|224083}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III {{MR|1931083}} {{MR|1532744}} {{MR|0155257}} {{ZBL|1008.57001}} {{ZBL|0103.15101}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) {{MR|0229247}} {{ZBL|0144.44804}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) {{MR|0533884}} {{ZBL|0444.32004}} </TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) {{MR|1335917}} {{MR|0202713}} {{ZBL|0376.14001}} </TD></TR></table> | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
| − | For more on the universality and classifying properties of the bundles | + | For more on the universality and classifying properties of the bundles $ \gamma ^ {k} $ |
| + | and $ \gamma _ {k} $ | ||
| + | cf. [[Classifying space|Classifying space]] or [[#References|[a1]]]. | ||
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) {{MR|0440554}} {{ZBL|0298.57008}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) {{MR|0440554}} {{ZBL|0298.57008}} </TD></TR></table> | ||
Revision as of 08:28, 6 June 2020
A fibre space $ \pi : X \rightarrow B $
each fibre $ \pi ^ {-} 1 ( b) $
of which is endowed with the structure of a (finite-dimensional) vector space $ V $
over a skew-field $ {\mathcal P} $
such that the following local triviality condition is satisfied. Each point $ b \in B $
has an open neighbourhood $ U $
and an $ U $-
isomorphism of fibre bundles $ \phi : \pi ^ {-} 1 ( U) \rightarrow U \times V $
such that $ \phi \mid _ {\pi ^ {-} 1 ( b) } : \pi ^ {-} 1 ( b) \rightarrow b \times V $
is an isomorphism of vector spaces for each $ b \in B $;
$ \mathop{\rm dim} V $
is said to be the dimension of the vector bundle. The sections of a vector bundle $ \pi $
form a locally free module $ \Gamma ( \pi ) $
over the ring of continuous functions on $ B $
with values in $ {\mathcal P} $.
A morphism of vector bundles is a morphism of fibre bundles $ f: \pi \rightarrow \pi ^ \prime $
for which the restriction to each fibre is linear. The set of vector bundles and their morphisms forms the category $ \mathbf{Bund} $.
The concept of a vector bundle arose as an extension of the tangent bundle and the normal bundle in differential geometry; by now it has become a basic tool for studies in various branches of mathematics: differential and algebraic topology, the theory of linear connections, algebraic geometry, the theory of (pseudo-) differential operators, etc.
A subset $ X ^ \prime \subset X $ such that $ \pi \mid _ {X} ^ \prime : X ^ \prime \rightarrow B $ is a vector bundle and $ X ^ \prime \cap \pi ^ {-} 1 ( b) $ is a vector subspace in $ \pi ^ {-} 1 ( b) $ is said to be a subbundle of the vector bundle $ \pi $. For instance, let $ V $ be a vector space and let $ G _ {k} ( V) $ be the Grassmann manifold of subspaces of $ V $ of dimension $ k $; the subspace of the product $ G _ {k} ( V) \times V $, consisting of pairs $ ( p, v) $ such that $ v \in p $, will then be a subbundle $ \gamma _ {k} $ of the trivial vector bundle $ G _ {k} ( V) \times V $. The union of all vector spaces $ \pi ^ {-} 1 ( b) / \pi _ {2} ^ {-} 1 ( b) $, where $ \pi _ {2} $ is a subbundle of $ \pi $ endowed with the quotient topology, is said to be a quotient bundle of $ \pi $. Let, furthermore, $ V $ be a vector space and let $ G ^ {k} ( V) $ be the Grassmann manifold of subspaces of $ V $ of codimension $ k $; the quotient bundle $ \gamma ^ {k} $ of the trivial vector bundle $ G ^ {k} ( V) \times V $ is defined as the quotient space of the product $ G ^ {k} ( V) \times V $ by the subbundle consisting of all pairs $ ( p, v) $, $ v \in p $. The concepts of a subbundle and a quotient bundle are used in contraction and glueing operations used to construct vector bundles over quotient spaces.
A $ B $- morphism of vector bundles $ f : \pi \rightarrow \pi ^ \prime $ is said to be of constant rank (pure) if $ \mathop{\rm dim} \mathop{\rm ker} f \ \mid _ {\pi ^ {-} 1 ( b) } $ is locally constant on $ B $. Injective and surjective morphisms are exact and are said to be monomorphisms and epimorphisms of the vector bundle, respectively. The following vector bundles are uniquely defined for a morphism $ f $ of locally constant rank: $ \mathop{\rm Ker} f $( the kernel of $ f $), which is a subbundle of $ \pi $; $ \mathop{\rm Im} f $( the image of $ f $), which is a subbundle of $ \pi ^ \prime $; $ \mathop{\rm Coker} f $( the cokernel of $ f $), which is a quotient bundle of $ \pi $; and $ \mathop{\rm Coim} f $( the co-image of $ f $), which is a quotient bundle of $ \pi ^ \prime $. Any subbundle $ \pi _ {1} $ is the image of some monomorphism $ i: \pi _ {1} \rightarrow \pi $, while any quotient bundle $ \pi _ {2} $ is the cokernel of some epimorphism $ j : \pi \rightarrow \pi _ {2} $. A sequence of $ B $- morphisms of vector bundles
$$ {} \dots \rightarrow \pi ^ \prime \rightarrow \pi \rightarrow \pi ^ {\prime\prime} \rightarrow \dots $$
is said to be exact if the sequence
$$ {} \dots \rightarrow ( \pi ^ \prime ) ^ {-} 1 ( b) \rightarrow \pi ^ {-} 1 ( b) \rightarrow ( \pi ^ {\prime\prime} ) ^ {-} 1 ( b) \rightarrow \dots $$
is exact for all $ b \in B $. In particular, the sequence
$$ 0 \rightarrow \pi _ {1} \rightarrow ^ { i } \pi \rightarrow ^ { j } \pi _ {2} \rightarrow 0 , $$
where $ 0 $ is the zero vector bundle, is exact if $ i $ is a monomorphism, $ j $ is an epimorphism and $ \mathop{\rm Im} i = { \mathop{\rm Ker} } j $. The set of vector bundles over $ B $ and $ B $- morphisms of locally constant rank forms an exact subcategory $ \mathbf{Bund} _ {B} $ of the category $ \mathbf{Bund} $.
For any vector bundle $ \pi : X \rightarrow B $ and mapping $ u: B _ {1} \rightarrow B $, the induced fibre bundle $ u ^ {*} ( \pi ) $ is endowed with a vector bundle structure such that the morphism $ U: u ^ {*} ( \pi ) \rightarrow \pi $ is a vector bundle morphism. This structure is unique and has the following property: Every fibre mapping $ {( u ^ {*} ( \pi )) } ^ {-} 1 ( b) \rightarrow \pi ^ {-} 1 ( u( b)) $ is an isomorphism of vector spaces. For instance, a vector bundle of dimension $ k $ over a paracompact space $ B $ is isomorphic to one of the vector bundles $ u ^ {*} ( \gamma _ {k} ) $ and $ \widetilde{u} {} ^ {*} ( \gamma ^ {k} ) $ induced by certain mappings $ u: B \rightarrow G _ {k} ( V) $ and $ \widetilde{u} : B \rightarrow G ^ {k} ( V) $, respectively; moreover, homotopic mappings induce isomorphic vector bundles and, if $ \mathop{\rm dim} V \neq \infty $, the converse is true: To isomorphic vector bundles there correspond homotopic mappings $ u $ and $ \widetilde{u} $. This is one of the fundamental theorems in the homotopic classification of vector bundles, expressing the universal character of the vector bundles $ \gamma _ {k} $ and $ \gamma ^ {k} $ with respect to the classifying mappings $ u $ and $ \widetilde{u} $.
Any continuous operation (functor) $ T $ on the category of vector spaces uniquely determines a continuous functor on the category of vector bundles over $ B $; in this way it is possible to construct bundles associated with a given vector bundle: tensor bundles, vector bundles of morphisms $ { \mathop{\rm Hom} } _ {B} ( \pi , \pi ^ \prime ) $ and, in particular, the dual vector bundle $ \pi ^ {*} $, exterior powers of vector bundles, etc., whose sections are vector bundles with supplementary structures. These are extensively employed in practical applications.
A direct sum (Whitney sum) $ \pi \oplus \pi ^ \prime $ and tensor product $ \pi \otimes \pi ^ \prime $ have been defined for two vector bundles $ \pi $ and $ \pi ^ \prime $. With respect to these operations the set of classes $ { \mathop{\rm Vekt} } _ {B} $ of isomorphic vector bundles over $ B $ forms a semi-ring which plays an important part in the construction of a $ K $- functor; thus, if for vector bundles $ \pi $ and $ \pi ^ \prime $ there exist trivial vector bundles $ \theta $ and $ \theta ^ \prime $ such that the vector bundles $ \pi \oplus \theta $ and $ \pi ^ \prime \oplus \theta ^ \prime $ are isomorphic (i.e. $ \pi $ and $ \pi ^ \prime $ are stably equivalent), then their images in the "completion" $ K ( B) $ of the semi-ring $ { \mathop{\rm Vekt} } _ {B} $ are identical; moreover, the fact that the ring $ K( B) $ and the set of classes of stably-equivalent vector bundles coincide follows from the existence of an inverse vector bundle for any vector bundle over a paracompact space.
For any vector bundle $ \pi : X \rightarrow B $ over a paracompact space $ B $ there exists a section $ \beta $ of the vector bundle
$$ \pi ^ {*} \oplus \pi ^ {*} = \mathop{\rm Hom} ( \pi \oplus \pi , P ), $$
where $ P $ is a trivial one-dimensional vector bundle, which on each fibre $ \pi ^ {-} 1 ( b) $ is a positive-definite form, i.e. $ \pi $ is metrizable; this makes it possible to establish, in particular, the splittability of an arbitrary exact sequence of vector bundles
$$ 0 \rightarrow \xi \rightarrow ^ { u } \pi \rightarrow ^ { v } \zeta \rightarrow 0 $$
in which $ \pi $ is metrizable, that is, the existence of a morphism $ w : \xi \oplus \zeta \rightarrow \pi $ such that $ wi = u $, $ vw = j $, where $ i $ is the imbedding into the first term and $ j $ is the projection onto the second term.
If, in each fibre $ \pi ^ {-} 1 ( b) $ of the vector bundle $ \pi : X \rightarrow B $, one identifies the points lying on the same line passing through zero, one obtains a bundle $ \pi _ {0} : \Pi _ {( \pi ) } \rightarrow B $, which is associated with $ \pi $ and is said to be its projectivization; a fibre of $ \pi _ {0} $ is the projective space $ \Pi ( V) $ which is associated with $ V $. This bundle is used to study Thom spaces $ T ( \pi ) = \Pi ( \pi \oplus P)/ \Pi ( \pi ) $( cf. Thom space), used in the homotopic interpretation of classes of bordant manifolds, characteristic classes of vector bundles describing the homological properties of manifolds, etc.
The concept of a vector bundle can be generalized to the case when the fibre is an infinite-dimensional vector space; in doing so, one must distinguish between the different topologies of the space of morphisms $ { \mathop{\rm Hom} } ( \pi , \pi ^ \prime ) $, suitably modify the definitions of a pure morphism and an exact sequence of morphisms, and also the construction of vector bundles associated with continuous functors on the category of infinite-dimensional vector spaces.
References
| [1] | C. Godbillon, "Géométrie différentielle et mécanique analytique" , Hermann (1969) MR0242081 Zbl 0653.53001 Zbl 0284.53018 |
| [2] | M.F. Atiyah, "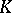 -theory: lectures" , Benjamin (1967) MR224083 -theory: lectures" , Benjamin (1967) MR224083 |
| [3] | S. Lang, "Introduction to differentiable manifolds" , Interscience (1967) pp. App. III MR1931083 MR1532744 MR0155257 Zbl 1008.57001 Zbl 0103.15101 |
| [4] | D. Husemoller, "Fibre bundles" , McGraw-Hill (1966) MR0229247 Zbl 0144.44804 |
| [5] | S.S. Chern, "Complex manifolds without potential theory" , Springer (1979) MR0533884 Zbl 0444.32004 |
| [6] | F. Hirzebruch, "Topological methods in algebraic geometry" , Springer (1978) (Translated from German) MR1335917 MR0202713 Zbl 0376.14001 |
Comments
For more on the universality and classifying properties of the bundles $ \gamma ^ {k} $ and $ \gamma _ {k} $ cf. Classifying space or [a1].
References
| [a1] | J.W. Milnor, J.D. Stasheff, "Characteristic classes" , Princeton Univ. Press (1974) MR0440554 Zbl 0298.57008 |
Vector bundle. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Vector_bundle&oldid=24005