Difference between revisions of "Lobachevskii function"
(Importing text file) |
|||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | <!-- | |
| + | l0600201.png | ||
| + | $#A+1 = 19 n = 0 | ||
| + | $#C+1 = 19 : ~/encyclopedia/old_files/data/L060/L.0600020 Lobachevski\Aui function | ||
| + | Automatically converted into TeX, above some diagnostics. | ||
| + | Please remove this comment and the {{TEX|auto}} line below, | ||
| + | if TeX found to be correct. | ||
| + | --> | ||
| − | + | {{TEX|auto}} | |
| + | {{TEX|done}} | ||
| − | + | == Angle of parallelism == | |
| + | |||
| + | The angle of parallelism in [[Lobachevskii geometry]] is a function that expresses the angle $ \alpha $ | ||
| + | between the line $ u _ {1} $ (or $ u _ {2} $) | ||
| + | (see Fig.) and the segment $ OA $ | ||
| + | perpendicular to a line $ a $ | ||
| + | parallel to $ u _ {1} $( | ||
| + | or $ u _ {2} $) | ||
| + | in terms of the length $ l $ | ||
| + | of the segment $ OA $: | ||
| + | |||
| + | $$ | ||
| + | \alpha = \Pi(l) = 2 { \mathop{\rm arc} \mathop{\rm tan} } e ^ {- l / R } , | ||
| + | $$ | ||
| + | |||
| + | where $R$ is a positive constant that corresponds to the scale of measurement of distances. | ||
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/l060020a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/l060020a.gif" /> | ||
| Line 9: | Line 32: | ||
Figure: l060020a | Figure: l060020a | ||
| − | The Lobachevskii function is a continuous monotone decreasing function with values between | + | The Lobachevskii function is a continuous monotone decreasing function with values between $\pi/2$ and 0: |
| − | + | $$ | |
| + | \lim\limits _ {l \rightarrow 0 } \Pi ( l) = | ||
| + | \frac \pi {2} | ||
| + | ,\ \lim\limits _ { | ||
| + | l \rightarrow \infty } \Pi ( l) = 0. | ||
| + | $$ | ||
It was introduced by N.I. Lobachevskii in 1826. | It was introduced by N.I. Lobachevskii in 1826. | ||
| − | ==== | + | == Second meaning == |
| − | |||
| − | The special function (cf. [[ | + | The special function (cf. [[Special functions]]) defined for real $x$ |
| + | by | ||
| − | + | $$ | |
| + | L(x) = - \int\limits_{0}^{x} \mathop{\rm ln} \cos t dt . | ||
| + | $$ | ||
The Lobachevskii function can be represented as a series | The Lobachevskii function can be represented as a series | ||
| − | + | $$ | |
| + | L(x) = x \mathop{\rm ln} 2 - \frac{1}{2} | ||
| + | \sum _ { k= 1} ^ {\infty } (- 1) ^ {k- 1} \frac{\sin 2kx }{k ^ {2} } . | ||
| + | $$ | ||
The main relations are: | The main relations are: | ||
| − | + | $$ | |
| + | L ( - x ) = - L ( x) ,\ - \frac \pi {2} \leq x \leq \frac \pi {2}, | ||
| + | $$ | ||
| − | + | $$ | |
| + | L ( \pi - x ) = \pi \mathop{\rm ln} 2 - L ( x) , | ||
| + | $$ | ||
| − | + | $$ | |
| + | L ( \pi + x ) = \pi \mathop{\rm ln} 2 + L ( x) . | ||
| + | $$ | ||
It was introduced by N.I. Lobachevskii in 1829. | It was introduced by N.I. Lobachevskii in 1829. | ||
| − | + | ==Comments== | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
For the Lobachevskii function in the sense of 1) (i.e. the angle of parallelism) see also [[#References|[a1]]]–[[#References|[a4]]]. | For the Lobachevskii function in the sense of 1) (i.e. the angle of parallelism) see also [[#References|[a1]]]–[[#References|[a4]]]. | ||
For Lobachevskii's function as defined in 2) see also [[#References|[a5]]]. | For Lobachevskii's function as defined in 2) see also [[#References|[a5]]]. | ||
| − | ==== | + | ==References== |
| − | < | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.F. Kagan, "Foundations of geometry" , '''1''' , Moscow-Leningrad (1949) (In Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian)</TD></TR> |
| + | <TR><TD valign="top">[1]</TD> <TD valign="top"> I.M. Ryzhik, I.S. Gradshtein, "Tables of integrals, series, and products" , Acad. Press (1980) (Translated from Russian)</TD></TR> | ||
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> H.S.M. Coxeter, "Parallel lines" ''Canad. Math. Bull.'' , '''21''' (1978) pp. 385–397</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1957)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R. Bonola, "Non-Euclidean geometry" , Dover, reprint (1955) (Translated from Italian)</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> H.S.M. Coxeter, "Twelve geometric esays" , Carbondale (1968) pp. Chapt. 1</TD></TR></table> | ||
| + | |||
| + | {{OldImage}} | ||
Latest revision as of 12:22, 1 May 2023
Angle of parallelism
The angle of parallelism in Lobachevskii geometry is a function that expresses the angle $ \alpha $ between the line $ u _ {1} $ (or $ u _ {2} $) (see Fig.) and the segment $ OA $ perpendicular to a line $ a $ parallel to $ u _ {1} $( or $ u _ {2} $) in terms of the length $ l $ of the segment $ OA $:
$$ \alpha = \Pi(l) = 2 { \mathop{\rm arc} \mathop{\rm tan} } e ^ {- l / R } , $$
where $R$ is a positive constant that corresponds to the scale of measurement of distances.
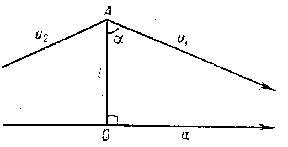
Figure: l060020a
The Lobachevskii function is a continuous monotone decreasing function with values between $\pi/2$ and 0:
$$ \lim\limits _ {l \rightarrow 0 } \Pi ( l) = \frac \pi {2} ,\ \lim\limits _ { l \rightarrow \infty } \Pi ( l) = 0. $$
It was introduced by N.I. Lobachevskii in 1826.
Second meaning
The special function (cf. Special functions) defined for real $x$ by
$$ L(x) = - \int\limits_{0}^{x} \mathop{\rm ln} \cos t dt . $$
The Lobachevskii function can be represented as a series
$$ L(x) = x \mathop{\rm ln} 2 - \frac{1}{2} \sum _ { k= 1} ^ {\infty } (- 1) ^ {k- 1} \frac{\sin 2kx }{k ^ {2} } . $$
The main relations are:
$$ L ( - x ) = - L ( x) ,\ - \frac \pi {2} \leq x \leq \frac \pi {2}, $$
$$ L ( \pi - x ) = \pi \mathop{\rm ln} 2 - L ( x) , $$
$$ L ( \pi + x ) = \pi \mathop{\rm ln} 2 + L ( x) . $$
It was introduced by N.I. Lobachevskii in 1829.
Comments
For the Lobachevskii function in the sense of 1) (i.e. the angle of parallelism) see also [a1]–[a4].
For Lobachevskii's function as defined in 2) see also [a5].
References
| [1] | V.F. Kagan, "Foundations of geometry" , 1 , Moscow-Leningrad (1949) (In Russian) |
| [2] | N.V. Efimov, "Höhere Geometrie" , Deutsch. Verlag Wissenschaft. (1960) (Translated from Russian) |
| [1] | I.M. Ryzhik, I.S. Gradshtein, "Tables of integrals, series, and products" , Acad. Press (1980) (Translated from Russian) |
| [a1] | M. Greenberg, "Euclidean and non-Euclidean geometries" , Freeman (1974) |
| [a2] | H.S.M. Coxeter, "Parallel lines" Canad. Math. Bull. , 21 (1978) pp. 385–397 |
| [a3] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1957) |
| [a4] | R. Bonola, "Non-Euclidean geometry" , Dover, reprint (1955) (Translated from Italian) |
| [a5] | H.S.M. Coxeter, "Twelve geometric esays" , Carbondale (1968) pp. Chapt. 1 |
Lobachevskii function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lobachevskii_function&oldid=15981